Dieser Radius ist senkrecht zum größten Radius, aber Sie müssen für dieses Problem keine Winkel messen. Sie können diesen Radius auch als "kleine Hauptachse" bezeichnen. 
Wenn eine Ellipse beispielsweise einen größten Radius von 5 und einen kleinsten Radius von 3 hat, beträgt die Fläche der Ellipse 3 x 5 x π oder ungefähr 47 Quadrateinheiten. Wenn Sie keinen Taschenrechner haben oder wenn Ihr Taschenrechner kein π-Symbol hat, verwenden Sie `3.14` als Wert für pi. 

Berechnen sie die fläche einer ellipse
Eine Ellipse ist eine zweidimensionale Form, die Sie vielleicht bereits aus dem Geometrieunterricht kennen und die wie ein länglicher Kreis aussieht. Die Berechnung der Fläche einer Ellipse ist einfach, wenn Sie die Länge des größten Radius und des kleinsten Radius kennen.
Schritte
Teil 1 von 2: Flächenberechnung

1. Finden Sie den größten Radius der Ellipse. Dies ist der Abstand vom Mittelpunkt der Ellipse zum äußersten Rand der Ellipse. Betrachten Sie dies als den Radius des `dicken` Teils der Ellipse. Messen Sie dies oder suchen Sie in der Tabelle nach dem entsprechenden Label. Wir nennen diesen Wert ein.
- Sie können dies auch die `große Hauptachse` nennen.

2. Finden Sie den kleinsten Radius. Wie Sie vielleicht erraten haben, ist der kleinste Radius der Abstand vom Mittelpunkt zum nächsten Punkt auf der Kante. Wir nennen diesen Wert B.

3. Mit pi . multiplizieren. Die Fläche der Ellipse beträgt ein x B x. Da Sie zwei Längeneinheiten miteinander multiplizieren, ist Ihre Antwort ein Quadrat.
Teil 2 von 2: Verstehen Sie, warum es funktioniert

1. Betrachten Sie die Fläche eines Kreises. Sie erinnern sich vielleicht, dass die Fläche eines Kreises gleichR, was dasselbe ist wie π x R x R. Angenommen, wir möchten die Fläche eines Kreises so bestimmen, als ob es eine Ellipse wäre? Wir messen den Radius in eine Richtung: R. Messen Sie es mit rechten Winkeln: auch R. Wende dies auf die Formel für die Fläche einer Ellipse an: π x r x r! Es stellt sich heraus, dass ein Kreis nur eine bestimmte Art von Ellipse ist.

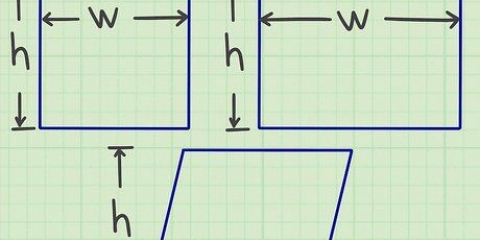
2. Stellen Sie sich einen abgeflachten Kreis vor. Stellen Sie sich vor, ein Kreis wird in Form einer Ellipse gedruckt. Wenn der Kreis immer weiter komprimiert wird, wird ein Radius kürzer und der andere länger. Die Fläche bleibt gleich, denn nichts geht aus dem Kreis. Solange wir beide Radien in der Gleichung verwenden, heben sich das `quetschen` und `dehnen` auf und wir erhalten immer noch die richtige Antwort.
Tipps
- Wenn du dafür einen mathematischen Beweis haben willst, musst du lernen integrieren.
"Berechnen sie die fläche einer ellipse"
Оцените, пожалуйста статью