Integrieren: 9 Schritte (mit Bildern)

Schritte
- Methode 1 von 2: Einfache Integration
- Methode 2 von 2: Andere Regeln

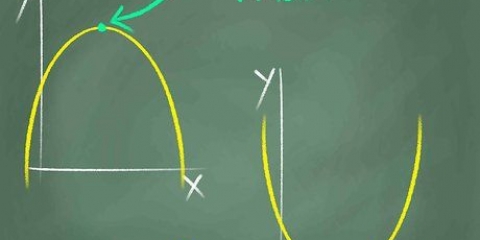
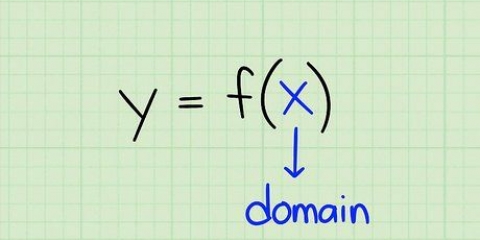
Integration ist die Umkehrung der Differenzierung innerhalb der Mathematik (Analyse). Es ist der Prozess der Berechnung der Fläche unter einer Kurve, die von einer xy-Ebene eingeschlossen ist. Je nach Art des Polynoms (Polynom), mit dem Sie es zu tun haben, gibt es unterschiedliche Regeln für die Integration.

Schritte

Methode 1 von 2: Einfache Integration

1. Die folgende einfache Integrationsregel funktioniert für fast alle Standardpolynome. Nimm das Polynom y = a*x^n.

2. Dividiere a (der Koeffizient) durch n+1 (die Potenz + 1) und erhöhe die Potenz um 1. Mit anderen Worten, das Integral von y = a*x^n ist y = (a/n+1)*x^(n+1).

3. Addiere die Konstante des Integrals C für unbekannte Integrale, um ihre inhärente Bedeutung in Bezug auf den genauen Wert zu korrigieren. Daher lautet die endgültige Antwort in diesem Fall y = (a/n+1)*x^(n+1) + C.

Stellen Sie sich das so vor: Wenn Sie die Ableitung einer Funktion berechnen, werden Konstanten einfach aus der endgültigen Antwort weggelassen. Daher ist es immer möglich, dass das Integral einer Funktion eine beliebige Konstante hat.

4. Integrieren Sie einzelne Teile einer Funktion mit der Regel. Zum Beispiel das Integral von y = 4x^3 + 5x^2 +3x ist (4/4)x^4 + (5/3)*x^3 + (3/2)*x^2 + C = x^4 + (5/3)*x^3 + (3/2)*x^2 + C.

Methode 2 von 2: Andere Regeln

1. Dieselben Regeln gelten nicht für x^-1 oder 1/x. Wenn Sie eine mit -1 potenzierte Variable integrieren, ist das Integral de natürlicher Logarithmus der Variablen. Mit anderen Worten, das Integral von (x+3)^-1 ist ln(x+3) + C.

2. Das Integral von e^x ist immer gleich sich selbst. Das Integral von e^(nx) ist 1/n * e^(nx) + C; somit ist das Integral von e^(4x) gleich 1/4 * e^(4x) + C.

3. Die Integration trigonometrischer Funktionen erfordert das Erlernen bestimmter Integrale. Denken Sie an die folgenden Integrale:

Das Integral von cos(x) ist sin(x) + C.

Das Integral von sin(x) ist -cos(x) + C. (beachte das Minuszeichen!)

Mit diesen beiden Regeln können Sie das Integral von tan(x) berechnen, das äquivalent zu sin(x)/cos(x) ist. Die Antwort ist -ln|cos x| + C - überprüfe deine Arbeit!

4. Bei komplexeren Polynomen wie (3x-5)^4 müssen Sie lernen, durch Substitution zu integrieren. Diese Technik führt eine Variable wie den Buchstaben u ein, die ein Polynom von Variablen wie 3x-5 darstellt, um den Prozess zu vereinfachen und gleichzeitig die gleichen Regeln für die Integration anzuwenden.