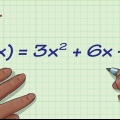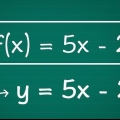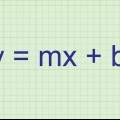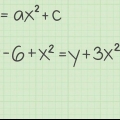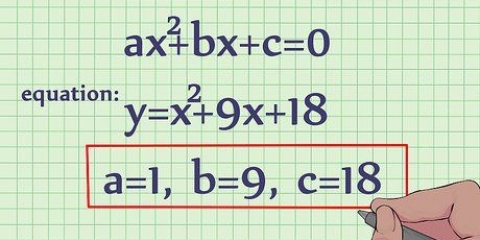Wenn der Wert von ein positiv ist, dann erhält man den minimalen Wert, da die Parabel oben offen ist (der Scheitelpunkt ist der tiefste Punkt des Graphen).
Wenn der Wert von ein negativ ist, finden Sie den Maximalwert, da die Parabel unten offen ist (der Scheitelpunkt ist der höchste Punkt des Graphen).
Der Wert von ein kann nicht null sein, sonst haben wir es nicht mit einer quadratischen Gleichung zu tun, richtig?







Bestimmung der maximal- und minimalwerte einer quadratischen funktion
Die y-Koordinate des Scheitels oder Tals einer Parabel (normalerweise durch k dargestellt) ist auch der maximale oder minimale Wert der quadratischen Gleichung, wie sie durch die Parabel dargestellt wird. Mal sehen, wie man es bestimmt!
Schritte
Methode 1 von 4: Für eine quadratische Gleichung der Form y = ax + bx + c

1. Entscheiden Sie, ob Sie den Maximalwert oder den Minimalwert ermitteln möchten. Es ist das eine oder das andere, man kann nicht beides machen.
- Der maximale oder minimale Wert einer quadratischen Gleichung ist der gleiche wie die Spitze oder das Tal dieser Funktion.
Die Funktion y = ax + bx + c,
(c - b/4a) gibt den y-Wert (den Wert der Funktion) als Scheitelpunkt zurück.




Methode 2 von 4: Für eine quadratische Gleichung in der Form y = a(x-h) + k

1. Für y = a(x-h) + k, k ist der Wert der Funktion am Scheitelpunkt.
- k gibt uns den maximalen oder minimalen Wert der quadratischen Gleichung an, wenn ein ist negativ bzw. positiv.

Methode 3 von 4: Differenziere nach einer quadratischen Gleichung der Form y = ax^2 + bx + c

1. Differenziere y nach x. dy/dx = 2ax + b

2. Bestimmen Sie die abgeleiteten Werte in Bezug auf dy/dx. Da dy/dx die Ableitungsfunktion einer Kurve ist, kann die Ableitung einer Kurve zu jedem beliebigen Zeitpunkt bestimmt werden. Der Maximal-/Minimalwert lässt sich also ermitteln, indem man diese Werte gleich 0 setzt und dann die entsprechenden Werte ermittelt. dy/dx = 0, 2ax+b = 0, x = -b/2a

3. Ersetzen Sie diesen Wert von x durch y für den minimalen/maximalen Wert.
Methode 4 von 4: Beispiele

1. Bestimmen Sie den maximalen oder minimalen Wert der Funktion f(x) = x + x + 1.

2. Bestimmen Sie den maximalen oder minimalen Wert der Funktion f(x) = -2(x-1) + 3.
Tipps
- Die Symmetrieachse der Parabel ist x = h.
- -h ist der Wert, der dem maximalen oder minimalen Wert entspricht.
"Bestimmung der maximal- und minimalwerte einer quadratischen funktion"
Оцените, пожалуйста статью