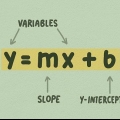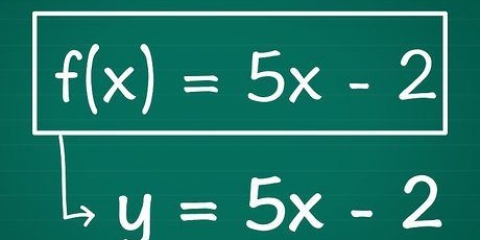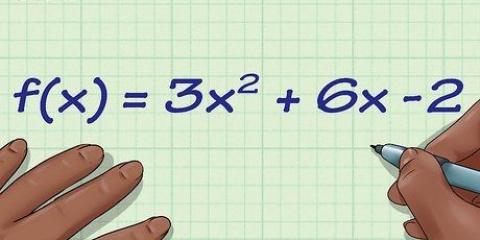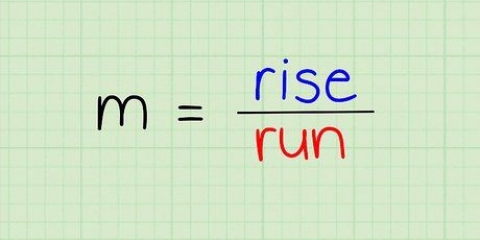Wenn die Steigung negativ ist, bedeutet dies, dass die Linie nach rechts abfällt. 





-1: -1 + 2 = 1 0: 0 +2 = 2 1: 1 + 2 = 3 




Machen Sie F(x) gleich Null:
Lösen:




Einige quadratische Funktionen, wie z  sind nie negativ. Es gibt also eine Asymptote bei 0.
sind nie negativ. Es gibt also eine Asymptote bei 0. Wenn Sie nicht mit imaginären Zahlen arbeiten, ist dies nicht möglich: 
Gleichungen mit komplexen Exponenten können viele Asymptoten haben. 
Zum Vergleich  , könnten Sie -1, 0, 1, -2, 2, -10 und 10 . ausfüllen. Dies gibt Ihnen eine schöne Reihe von Zahlen zum Vergleichen.
, könnten Sie -1, 0, 1, -2, 2, -10 und 10 . ausfüllen. Dies gibt Ihnen eine schöne Reihe von Zahlen zum Vergleichen. Seien Sie schlau bei der Auswahl von Zahlen. Im Beispiel werden Sie schnell feststellen, dass ein negatives Vorzeichen keine Rolle spielt – zum Beispiel können Sie den Test von -10 beenden, da es gleich 10 . ist. 
Nehmen Sie zwei bis vier große Werte für x an, halb negativ und halb positiv, und zeichnen Sie die Punkte. Was passiert, wenn Sie `unendlich` für eine Variable einfügen?? Wird die Funktion unendlich größer oder kleiner? Wenn die Grade in einem Bruch gleich sind, wie z  , dann dividiere einfach die ersten beiden Koeffizienten (
, dann dividiere einfach die ersten beiden Koeffizienten ( um Ihre endgültige Asymptote zu erhalten (-0.5).
um Ihre endgültige Asymptote zu erhalten (-0.5). Wenn die Grade in einem Bruch unterschiedlich sind, dividiere die Gleichung im Zähler durch die Gleichung im Nenner mit polynomialer langer Division. 

Den graphen einer funktion zeichnen
Ein Funktionsgraph ist eine visuelle Darstellung des Verhaltens einer Funktion auf einer x-y-Ebene. Graphen helfen uns, verschiedene Aspekte der Funktion zu verstehen, die nur durch einen Blick auf die Funktion selbst schwer zu verstehen wären. Sie können Tausende von Gleichungen grafisch darstellen, und für jede Gleichung gibt es unterschiedliche Formeln. Es gibt jedoch immer Möglichkeiten, eine Funktion grafisch darzustellen, wenn Sie die genauen Schritte für den jeweiligen Funktionstyp vergessen haben.
Schritte
Methode 1 von 3: Zeichnen Sie eine lineare Gleichung mit einer Tangente

1. Wisse, dass lineare Funktionen einfache Linien sind, die einfach zu zeichnen sind, wie z ja = 2 x + 5  . Es gibt eine Variable und eine Konstante, geschrieben als
. Es gibt eine Variable und eine Konstante, geschrieben als  in einer linearen Funktion, ohne Exponenten, Radikale usw. Wenn Sie eine so einfache Gleichung haben, ist der Graph der Funktion auch einfach. Andere Beispiele für lineare Funktionen sind:
in einer linearen Funktion, ohne Exponenten, Radikale usw. Wenn Sie eine so einfache Gleichung haben, ist der Graph der Funktion auch einfach. Andere Beispiele für lineare Funktionen sind:
 . Es gibt eine Variable und eine Konstante, geschrieben als
. Es gibt eine Variable und eine Konstante, geschrieben als  in einer linearen Funktion, ohne Exponenten, Radikale usw. Wenn Sie eine so einfache Gleichung haben, ist der Graph der Funktion auch einfach. Andere Beispiele für lineare Funktionen sind:
in einer linearen Funktion, ohne Exponenten, Radikale usw. Wenn Sie eine so einfache Gleichung haben, ist der Graph der Funktion auch einfach. Andere Beispiele für lineare Funktionen sind: 
2. Verwenden Sie die Konstante, um den Schnittpunkt mit der y-Achse anzugeben. Der Schnittpunkt mit der y-Achse ist der Punkt, an dem die Funktion die y-Achse in Ihrem Diagramm schneidet. Mit anderen Worten, es ist der Punkt, an dem  . Um es zu finden, setze einfach x auf Null und belasse die Konstante in der Gleichung. Im vorherigen Beispiel,
. Um es zu finden, setze einfach x auf Null und belasse die Konstante in der Gleichung. Im vorherigen Beispiel,  , ist der Schnittpunkt mit der y-Achse gleich y=5, d.h. der Punkt (0.5). Markieren Sie diese Stelle in Ihrem Diagramm mit einem Punkt.
, ist der Schnittpunkt mit der y-Achse gleich y=5, d.h. der Punkt (0.5). Markieren Sie diese Stelle in Ihrem Diagramm mit einem Punkt.
 . Um es zu finden, setze einfach x auf Null und belasse die Konstante in der Gleichung. Im vorherigen Beispiel,
. Um es zu finden, setze einfach x auf Null und belasse die Konstante in der Gleichung. Im vorherigen Beispiel,  , ist der Schnittpunkt mit der y-Achse gleich y=5, d.h. der Punkt (0.5). Markieren Sie diese Stelle in Ihrem Diagramm mit einem Punkt.
, ist der Schnittpunkt mit der y-Achse gleich y=5, d.h. der Punkt (0.5). Markieren Sie diese Stelle in Ihrem Diagramm mit einem Punkt.
3. Finden Sie die Steigung Ihrer Geraden mit der Zahl direkt vor der Variablen. Im Beispiel,  , ist die Steigung `2`. Das liegt daran, dass 2 zur Variablen `x` gehört. Die Steigung gibt an, wie steil eine Linie ist oder wie hoch die Linie ist, bevor sie nach rechts oder links abbiegt. Eine größere Steigung bedeutet eine steilere Linie.
, ist die Steigung `2`. Das liegt daran, dass 2 zur Variablen `x` gehört. Die Steigung gibt an, wie steil eine Linie ist oder wie hoch die Linie ist, bevor sie nach rechts oder links abbiegt. Eine größere Steigung bedeutet eine steilere Linie.
 , ist die Steigung `2`. Das liegt daran, dass 2 zur Variablen `x` gehört. Die Steigung gibt an, wie steil eine Linie ist oder wie hoch die Linie ist, bevor sie nach rechts oder links abbiegt. Eine größere Steigung bedeutet eine steilere Linie.
, ist die Steigung `2`. Das liegt daran, dass 2 zur Variablen `x` gehört. Die Steigung gibt an, wie steil eine Linie ist oder wie hoch die Linie ist, bevor sie nach rechts oder links abbiegt. Eine größere Steigung bedeutet eine steilere Linie.
4. Machen Sie einen Bruchteil der Steigung. Die Steigung hat mit der Steilheit zu tun, und die Steilheit ist einfach der Unterschied zwischen der Bewegung nach oben und unten sowie nach links und rechts. Die Steigung ist ein Bruchteil von die Änderung von y gegenüber der Änderung von x. Wie stark muss sich die Zeile `über y ändern`, bevor sie `über x ändern`? Im Beispiel kann die Steigung `2` gelesen werden als  .
.
 .
.
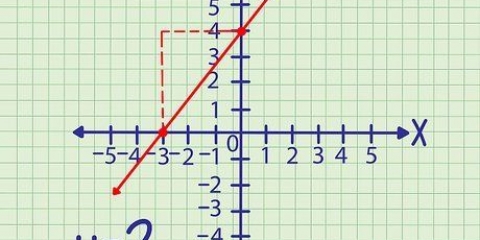
5. Beginnen Sie an Ihrem Schnittpunkt mit der y-Achse und folgen Sie den Änderungen über y und x, um weitere Punkte zu zeichnen. Sobald Sie die Steigung kennen, verwenden Sie sie, um Ihre lineare Funktion zu zeichnen. Beginnen Sie am Schnittpunkt mit der y-Achse, hier (0.5), gehen Sie dann nach oben 2 und nach rechts 1. Markieren Sie auch diesen Punkt (1,7). Finden Sie weitere 1-2 Punkte, um den Graphen zu zeichnen.

6. Verwenden Sie ein Lineal, um Ihre Punkte zu verbinden und Ihre lineare Funktion grafisch darzustellen. Um Fehler oder grobe Grafiken zu vermeiden, suchen und verbinden Sie mindestens drei separate Punkte, obwohl im Notfall zwei ausreichen. Dies ist der Graph Ihrer linearen Gleichung!
Methode 2 von 3: Schätzen von Punkten in einem Diagramm

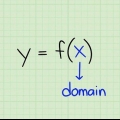
1. Bestimmen Sie die Funktion. Nimm die Funktion des Formulars F(x), wahr ja repräsentiert den Bereich, x stellt die Domäne dar, und F die Funktion. Als Beispiel verwenden wir ja = x+2, wodurch F(x) = x+2.

2. Zeichne zwei gekreuzte Linien auf ein Blatt Papier. Die horizontale Linie bist du x-Asche. Die vertikale Linie bist du ja-Asche.

3. Nummeriere dein Diagramm. Markieren Sie beide x-als ob die ja-Achse mit äquidistanten Zahlen. Für die x-Achse sind die Zahlen positiv rechts und negativ links. Für die ja-Achse sind die Zahlen oben positiv und unten negativ.

4. Berechnen Sie a ja-Wert für 2-3 x-Werte. Angenommen die Funktion F(x) = x+2. Berechnen Sie ein paar Werte für ja durch die entsprechenden Werte für x sichtbar an der Achse in der Funktion. Bei komplizierteren Gleichungen kann es notwendig sein, die Funktion zu vereinfachen, indem zuerst eine Variable isoliert wird.

5. Zeichnen Sie den Graphenpunkt für jedes Paar. Zeichnen Sie imaginäre dünne vertikale Linien entlang der x-Achse und horizontal entlang der ja-Asche. Der Punkt, an dem sich diese Linien schneiden, ist ein Diagrammpunkt (oder verwenden Sie einfach Millimeterpapier).

6. Entferne die imaginären Linien. Wenn Sie alle Diagrammpunkte gezeichnet haben, können Sie die imaginären Linien löschen. Hinweis: der Graph von f(x) = x wäre eine Linie parallel dazu durch den Ursprung (0,0), aber f(x) = x+2 ist um zwei Einheiten (entlang der y-Achse) auf dem Gitter verschoben wegen der +2 in der Gleichung.
Methode 3 von 3: Eine komplexe Funktion grafisch darstellen

1. Verstehen, wie gängige Gleichungstypen grafisch dargestellt werden. Es gibt so viele verschiedene Charting-Strategien wie es Arten von Funktionen gibt, viel zu viele, um sie hier vollständig abzudecken. Wenn Sie dies schwierig finden und eine Schätzung nicht funktioniert, lesen Sie Artikel zu:
- Quadratische Funktionen
- Rationale Funktionen
- Logarithmische Funktionen
- Ungleichungen (keine Funktionen, aber dennoch nützliche Informationen).

2.Bestimme zuerst die Nullstellen. Nullen sind die Punkte, an denen der Graph die horizontale Linie auf dem Graphen schneidet. Obwohl nicht alle Diagramme Nullen haben, tun dies die meisten, und dies ist der erste Schritt, den Sie unternehmen müssen, um alles richtig zu machen. Um Nullen zu finden, setze zuerst die ganze Funktion auf Null und löse sie dann. Zum Beispiel:







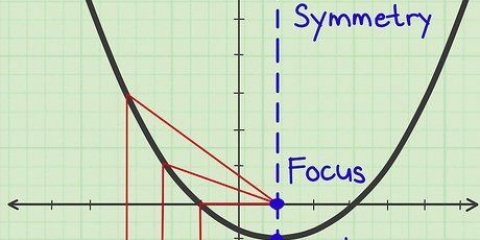
3. Suchen und markieren Sie alle horizontalen Asymptoten (Stellen, an denen die Funktion nicht zu erreichen ist) mit einer gestrichelten Linie. Dies sind normalerweise Punkte, an denen der Graph nicht existiert, z. B. wo Sie durch Null dividieren. Wenn Ihre Gleichung eine Variable in einem Bruch enthält, wie z  , dann beginne damit, den unteren Rand des Bruchs auf Null zu setzen. Sie können alle Stellen abbilden, an denen es gleich Null ist (in diesem Beispiel eine gestrichelte Linie bei x=2 und x=-2), da Sie niemals durch Null teilen können. Brüche sind jedoch nicht die einzigen Orte, an denen Asymptoten gefunden werden. Normalerweise braucht man nur etwas gesunden Menschenverstand:
, dann beginne damit, den unteren Rand des Bruchs auf Null zu setzen. Sie können alle Stellen abbilden, an denen es gleich Null ist (in diesem Beispiel eine gestrichelte Linie bei x=2 und x=-2), da Sie niemals durch Null teilen können. Brüche sind jedoch nicht die einzigen Orte, an denen Asymptoten gefunden werden. Normalerweise braucht man nur etwas gesunden Menschenverstand:
 , dann beginne damit, den unteren Rand des Bruchs auf Null zu setzen. Sie können alle Stellen abbilden, an denen es gleich Null ist (in diesem Beispiel eine gestrichelte Linie bei x=2 und x=-2), da Sie niemals durch Null teilen können. Brüche sind jedoch nicht die einzigen Orte, an denen Asymptoten gefunden werden. Normalerweise braucht man nur etwas gesunden Menschenverstand:
, dann beginne damit, den unteren Rand des Bruchs auf Null zu setzen. Sie können alle Stellen abbilden, an denen es gleich Null ist (in diesem Beispiel eine gestrichelte Linie bei x=2 und x=-2), da Sie niemals durch Null teilen können. Brüche sind jedoch nicht die einzigen Orte, an denen Asymptoten gefunden werden. Normalerweise braucht man nur etwas gesunden Menschenverstand: sind nie negativ. Es gibt also eine Asymptote bei 0.
sind nie negativ. Es gibt also eine Asymptote bei 0.

4. Übernehmen Sie die Werte und zeichnen Sie verschiedene Punkte. Wählen Sie einfach ein paar Werte für x aus und lösen Sie nach der Funktion auf. Dann zeichne ein Diagramm der Punkte auf deinem Diagramm. Je komplizierter die Grafik, desto mehr Punkte benötigen Sie. Im Allgemeinen sind -1, 0 und 1 die am einfachsten zu erreichenden Punkte, obwohl Sie zwei oder drei weitere auf jeder Seite der Null haben möchten, um eine gute Grafik zu erhalten.
 , könnten Sie -1, 0, 1, -2, 2, -10 und 10 . ausfüllen. Dies gibt Ihnen eine schöne Reihe von Zahlen zum Vergleichen.
, könnten Sie -1, 0, 1, -2, 2, -10 und 10 . ausfüllen. Dies gibt Ihnen eine schöne Reihe von Zahlen zum Vergleichen.
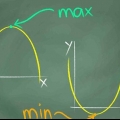
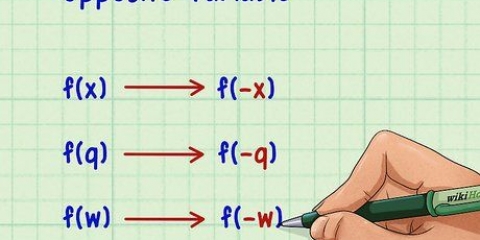
5. Ordnen Sie das Endverhalten der Funktion zu, um zu sehen, was passiert, wenn sie wirklich groß wird. Dies gibt Ihnen eine Vorstellung von der allgemeinen Richtung einer Funktion, normalerweise als a vertikal Asymptote. Zum Beispiel: das weißt du  wird irgendwann sehr, sehr groß. Nur ein zusätzliches `x` (eine Million gegenüber einer Million und eins) macht y viel größer. Es gibt mehrere Möglichkeiten, das Endverhalten zu testen, darunter:
wird irgendwann sehr, sehr groß. Nur ein zusätzliches `x` (eine Million gegenüber einer Million und eins) macht y viel größer. Es gibt mehrere Möglichkeiten, das Endverhalten zu testen, darunter:
 wird irgendwann sehr, sehr groß. Nur ein zusätzliches `x` (eine Million gegenüber einer Million und eins) macht y viel größer. Es gibt mehrere Möglichkeiten, das Endverhalten zu testen, darunter:
wird irgendwann sehr, sehr groß. Nur ein zusätzliches `x` (eine Million gegenüber einer Million und eins) macht y viel größer. Es gibt mehrere Möglichkeiten, das Endverhalten zu testen, darunter: , dann dividiere einfach die ersten beiden Koeffizienten (
, dann dividiere einfach die ersten beiden Koeffizienten ( um Ihre endgültige Asymptote zu erhalten (-0.5).
um Ihre endgültige Asymptote zu erhalten (-0.5).
6. Verbinden Sie die Punkte und vermeiden Sie asymptotisches Verhalten und Endverhalten, um den Graphen zu schätzen. Sobald Sie fünf oder sechs Punkte, die Asymptoten und eine allgemeine Vorstellung vom Endverhalten haben, verwenden Sie alle diese, um eine ungefähre Version des Graphen zu konstruieren.

7. Erstellen Sie perfekte Grafiken mit einem Grafikrechner. Grafikrechner sind leistungsstarke Handheld-Computer, die exakte Grafiken für jede Gleichung liefern können. Sie ermöglichen es Ihnen, exakte Punkte zu lokalisieren, Steigungslinien zu finden und schwierige Gleichungen mit Leichtigkeit zu visualisieren. Geben Sie einfach die genaue Gleichung in den Graphenbereich ein (normalerweise eine Schaltfläche mit der Bezeichnung `F(x) = `) und drücken Sie die Graphentaste, um sich ein Bild von der Funktion zu machen.
Tipps
- Graphische Taschenrechner sind eine großartige Möglichkeit zum Üben. Versuchen Sie, ein Diagramm von Hand zu erstellen und verwenden Sie dann den Taschenrechner, um ein perfektes Bild von dem Diagramm zu erhalten, und vergleichen Sie dann beide Diagramme.
- Wenn Sie wirklich nicht mehr wissen, was Sie tun sollen, geben Sie einfach ein paar Punkte ein. Grundsätzlich könnte man die ganze Funktion so zeichnen, wenn man unendlich viele Zahlenkombinationen ausprobiert.
Оцените, пожалуйста статью