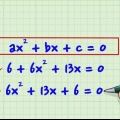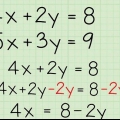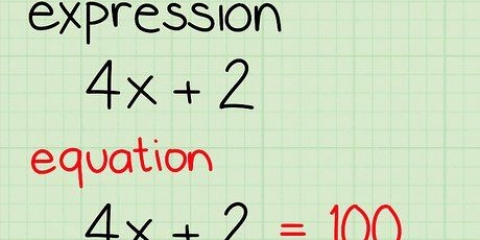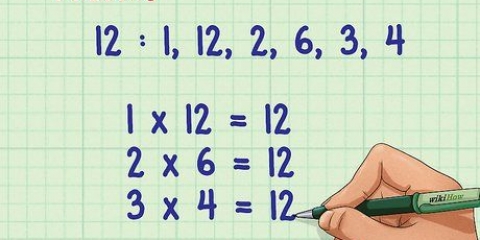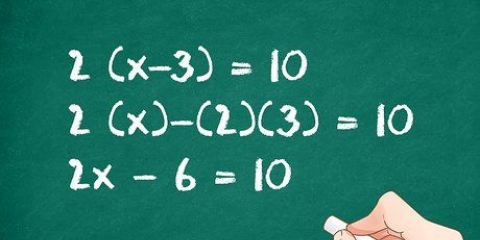Da 3x eine endliche Anzahl möglicher Faktoren hat, 3x und x, können Sie diese in Klammern schreiben: (3x +/- ? )(x +/-- ?) = 0. Verwenden Sie dann eine Eliminationsmethode, bei der Sie die Faktoren 4 verwenden, um eine Kombination zu finden, die als Ergebnis der Multiplikation -11x ergibt. Sie können entweder eine Kombination aus 4 und 1 oder 2 und 2 verwenden, da die Multiplikation beider Zahlenkombinationen 4 . ergibt. Denken Sie daran, dass einer der Terme negativ sein muss, da der Term -4 . ist. Versuchen (3x +1)(x -4). Wenn Sie dies ausarbeiten, erhalten Sie - 3x -12x +x -4. Wenn Sie die Begriffe -12x und x kombinieren, erhalten Sie -11x, was der mittlere Begriff ist, den Sie erreichen wollten. Jetzt haben Sie diese quadratische Gleichung faktorisiert. Ein anderes Beispiel; wir versuchen eine Gleichung zu faktorisieren, die nicht funktioniert: (3x-2)(x+2) = 3x +6x -2x -4. Wenn Sie diese Begriffe kombinieren, erhalten Sie 3x -4x -4. Obwohl das Produkt von -2 und 2 gleich -4 ist, funktioniert der Mittelterm nicht, weil Sie nach -11x und nicht nach -4x gesucht haben. 

3x + 1 = 0 = 3x = -1 = 3x/3 = -1/3 x = -1/3 x - 4 = 0 x = 4 x = (-1/3, 4) 

Beide Lösungen funktionieren also getrennt und beide werden als funktionierend verifiziert und sind in zwei verschiedenen Lösungen korrekt. 



{-b +/-√ (b - 4ac)}/2 {-(-5) +/-√ ((-5) - 4(3)(-8))}/2(3) = {-(-5) +/-√ ((-5) - (-96))}/2(3) 
{-(-5) +/-√ ((-5) - (-96))}/2(3) = {5 +/-√(25 + 96)}/6 {5 +/-√(121)}/6 

(5 + 11)/6 (5 - 11)/6 
(5 + 11)/6 = 16/6 (5-11)/6 = -6/6 
16/6 = 8/3 -6/6 = -1 x = (-1, 8/3) 

2x - 12x - 9 = 0 2x - 12x = 9 
2x/2 - 12x/2 = 9/2 = x - 6x = 9/2 
-6/2 = -3 = (-3) = 9 = x - 6x + 9 = 9/2 + 9 


x = 3 +(√6)/2 x = 3 - (√6)/2)
Quadratische gleichungen lösen
Eine quadratische Gleichung ist eine Gleichung, bei der der größte Exponent einer Variablen zwei ist. Drei der am häufigsten verwendeten Methoden zum Lösen dieser Gleichungen sind: Faktorisieren, Verwenden der abc-Formel oder Dividieren des Quadrats. Wenn Sie wissen möchten, wie Sie diese Methoden beherrschen, folgen Sie einfach diesen Schritten.
Schritte
Methode 1 von 3: Factoring

1. Verschiebe alle Terme auf eine Seite der Gleichung. Der erste Schritt beim Faktorisieren besteht darin, alle Terme auf eine Seite der Gleichung zu verschieben, sodass x positiv bleibt. Wende die Additions- oder Subtraktionsoperation auf die Terme x, die Variable x und die Konstanten an und verschiebe sie auf diese Weise auf eine Seite der Gleichung, sodass auf der anderen Seite nichts übrig bleibt. So funktioniert das:
- 2x - 8x - 4 = 3x - x =
- 2x +x - 8x -3x - 4 = 0
- 3x - 11x = 0

2. Faktorisieren Sie den Ausdruck. Um den Ausdruck zu faktorisieren, müssen Sie die Faktoren von 3x und die Faktoren der Konstanten -4 faktorisieren, um sie zu multiplizieren, und dann addieren, um den Wert des mittleren Termes zu erhalten, -11. So geht`s:

3. Bestimmen Sie, dass jedes Klammerpaar gleich Null ist und behandeln sie als separate Gleichungen. Dies führt dazu, dass Sie zwei Werte für x finden, die beide die gesamte Gleichung gleich Null machen. Nachdem Sie die Gleichung faktorisiert haben, müssen Sie nur noch jedes Klammerpaar gleich Null setzen. Sie können also schreiben: 3x +1 = 0 und x - 4 = 0.

4. Löse jede Gleichung. In einer quadratischen Gleichung gibt es zwei gegebene Werte für x. Lösen Sie jede Gleichung separat, indem Sie die Variable isolieren und schreiben Sie die Ergebnisse von x. So geht`s:

5. Überprüfen Sie x = -1/3 Zoll (3x + 1)(x – 4) = 0:
Wir bekommen (3[-1/3] + 1)([-1/3] – 4) ?=? 0 ..... durch Ersetzen:(-1 + 1)(-4 1/3) ?=? 0 ..... durch Vereinfachen:(0)(-4 1/3) = 0 ..... durch Multiplikation: also 0=0 ..... Ja, x = -1/3 funktioniert
Wir bekommen (3[-1/3] + 1)([-1/3] – 4) ?=? 0 ..... durch Ersetzen:(-1 + 1)(-4 1/3) ?=? 0 ..... durch Vereinfachen:(0)(-4 1/3) = 0 ..... durch Multiplikation: also 0=0 ..... Ja, x = -1/3 funktioniert

6. Überprüfen Sie x = 4 Zoll (3x + 1)(x - 4) = 0:
Wir erhalten (3[4] + 1)([4] – 4) ?=? 0..... durch Ersetzen:(13)(4 – 4) ?=? 0 ..... durch Dimmen:(13)(0) = 0 ..... durch Multiplikation:0=0 ..... Ja, x = 4 funktioniert
Wir erhalten (3[4] + 1)([4] – 4) ?=? 0..... durch Ersetzen:(13)(4 – 4) ?=? 0 ..... durch Dimmen:(13)(0) = 0 ..... durch Multiplikation:0=0 ..... Ja, x = 4 funktioniert
Methode 2 von 3: Anwenden der Abc-Formel

1. Verschiebe alle Terme auf eine Seite der Gleichung und füge die gleichen Terme zusammen. Verschiebe alle Terme auf eine Seite des Gleichheitszeichens, wobei der Term x positiv bleibt. Schreiben Sie die Terme in absteigender Größenordnung, also kommt zuerst x gefolgt von x, dann die Konstante. So geht`s:
- 4x - 5x - 13 =x -5
- 4x - x - 5x - 13 +5 = 0
- 3x - 5x - 8 = 0

2. Schreiben Sie die abc-Formel auf. Das ist: {-b +/-√ (b - 4ac)}/2a

3. Bestimmen Sie die Werte von a, b und c in der quadratischen Gleichung. Die Variable ein ist der Koeffizient von x, B ist der Koeffizient von x und C ist die Konstante. Für die Gleichung 3x -5x - 8 = 0, a = 3, b = -5 und c = -8. Schreib das auf.

4. Setze die Werte von a, b und c in die Gleichung ein. Da Sie nun die Werte der drei Variablen kennen, können Sie sie einfach in die Gleichung einsetzen, wie wir hier zeigen:

5. Berechnung. Nach dem Ausfüllen der Zahlen arbeiten Sie das Problem weiter aus. Nachfolgend können Sie nachlesen, wie das weiter geht:

6. Vereinfachen Sie die Quadratwurzel. Ist die Zahl unter dem Wurzelzeichen ein perfektes Quadrat oder auch eine Quadratzahl, dann erhält man eine ganze Zahl mit der Quadratwurzel. In anderen Fällen vereinfachen Sie die Quadratwurzel so weit wie möglich. Wenn die Zahl negativ ist und Sie sicher sind, dass dies beabsichtigt ist, ist die Quadratwurzel der Zahl weniger einfach. In diesem Beispiel ist √(121) = 11. Sie können dann schreiben, dass x =(5 +/- 11)/6.

7. Nach positiven und negativen Zahlen auflösen. Sobald Sie die Quadratwurzel losgeworden sind, können Sie fortfahren, bis Sie die negativen und positiven Antworten für x . gefunden haben. Da Sie nun (5 +/- 11)/6 haben, können Sie die beiden Möglichkeiten aufschreiben:

8. Lösen Sie nach den positiven und negativen Antworten auf. Rechne weiter:

9. Vereinfachen. Zur Vereinfachung dividiere die Antworten durch die größte Zahl, die durch Zähler und Nenner teilbar ist. Teilen Sie also den ersten Bruch durch 2 und den zweiten durch 6 und Sie haben x . gelöst.
Methode 3 von 3: Das Quadrat aufteilen

1. Verschiebe alle Terme auf eine Seite der Gleichung. Stellen Sie sicher, dass ein von x ist positiv. So geht`s:
- 2x - 9 = 12x =
- 2x - 12x - 9 = 0
- In dieser Gleichung ein gleich 2, B ist -12, und C ist -9.

2. Verschiebe die Konstante C auf die andere Seite. Die Konstante ist der Zahlenwert ohne Variable. Verschiebe es auf die rechte Seite der Gleichung:

3. Teilen Sie die beiden Seiten durch den Koeffizienten der ein oder x-Term. Wenn x keinen Term davor hat und einen Koeffizienten mit dem Wert 1 hat, können Sie diesen Schritt überspringen. In diesem Fall müssen Sie alle Terme wie folgt durch 2 teilen:

4. Teil B mit zwei quadrieren Sie es und addieren Sie die Ergebnisse zu beiden Seiten des is-Zeichens.DerB in diesem Beispiel ist -6. So geht`s:

5. Beide Seiten vereinfachen. Faktorisieren Sie die Terme auf der linken Seite, um (x-3)(x-3) oder (x-3) zu erhalten. Fügen Sie die Terme rechts hinzu, um 9/2 + 9 oder 9/2 + 18/2 zu erhalten, was 27/2 . ergibt.

6. Finde die Quadratwurzel beider Seiten. Die Quadratwurzel von (x-3) ist einfach (x-3). Sie können die Quadratwurzel von 27/2 auch schreiben als ±√(27/2). Daher x - 3 = ±√(27/2).

7. Vereinfachen Sie die Quadratwurzel und lösen Sie nach x . auf. Um ±√(27/2) zu vereinfachen, suchen Sie nach einem perfekten Quadrat oder einer Quadratzahl mit den Zahlen 27 oder 2 oder in ihren Faktoren. Die Quadratzahl 9 kann in 27 gefunden werden, denn 9 x 3 = 27. Um 9 aus der Wurzel zu eliminieren, schreiben Sie es als separate Wurzel und vereinfachen Sie zu 3, der Quadratwurzel von 9. Lassen Sie √3 im Zähler des Bruchs, da er nicht als Faktor von 27 getrennt werden kann, und machen Sie 2 zum Nenner. Verschiebe dann die Konstante 3 von der linken Seite der Gleichung auf die rechte Seite und schreibe deine beiden Lösungen für x auf:
Tipps
- Wie Sie sehen, ist das Radikalzeichen noch nicht ganz verschwunden. Daher werden die Terme im Zähler nicht zusammengeführt (sie sind nicht gleichbedeutend). Es ist also sinnlos die Minus- und Pluspunkte zu teilen. Stattdessen sorgen wir durch das Teilen dafür, dass alle Gemeinsamkeiten verschwinden – aber "NUR" wenn der Faktor für beide Konstanten gleich ist, "UND" der Koeffizient der Quadratwurzel.
Оцените, пожалуйста статью