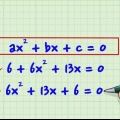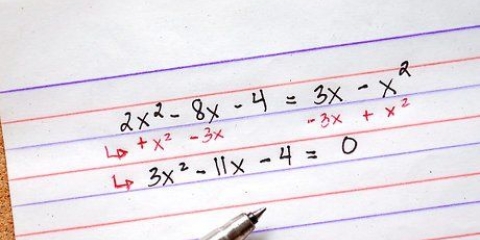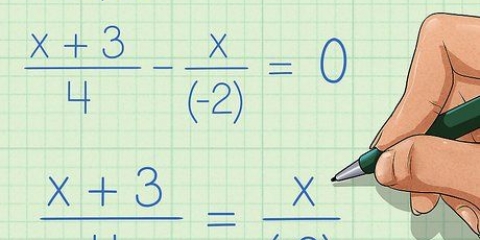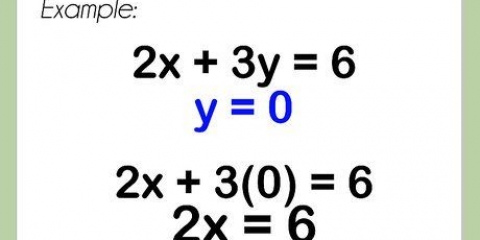Zum Beispiel: Wenn Sie 20 in Faktoren teilen möchten, können Sie das schreiben als 4×5. Beachten Sie, dass variable Terme auch als Faktoren geschrieben werden können. - Zum Beispiel kann 20x geschrieben werden als 4(5x). Primzahlen können nicht als Faktoren geschrieben werden, da sie nur durch sich selbst teilbar sind und 1. 
huhFledermäuse macht erhöhen Wzucken Vmultiplizieren Delen Özählen einsubtrahieren 

Suchen wir zum Beispiel die gleichen Terme in unserer Gleichung 1 + 2x - 3 + 4x. 2x und 4x haben beide dieselbe Potenz (in diesem Fall haben die x-Variablen überhaupt keinen Exponenten). Außerdem sind 1 und -3 gleiche Terme, da keiner eine Variable hat. In dieser Gleichung sind also 2x und 4x und 1 und -3 Augenhöhe. 
Wir addieren die gleichen Begriffe in unserem Beispiel. 2x + 4x = 6x 1 + -3 = -2 
In unserem Beispiel waren die vereinfachten Terme 6x und -2, also wird der neue Ausdruck 6x - 2. Dieser vereinfachte Ausdruck entspricht dem Original (1 + 2x - 3 + 4x), ist aber kürzer und einfacher zu berechnen mit. Es ist einfacher zu faktorisieren, was, wie wir weiter unten sehen werden, eine wichtige Fähigkeit ist, um zu vereinfachen. 
Angenommen, wir haben die Gleichung 5(3x-1) + x((2x)/(2)) + 8 - 3x. Dann wäre es falsch, 3x und 2x sofort als gleiche Terme zu betrachten und zu kombinieren, da die Klammern im Ausdruck vorschreiben, dass wir zuerst andere Operationen durchführen müssen. Führen wir zunächst die arithmetischen Operationen im Ausdruck gemäß der Reihenfolge der Operationen aus, um die Terme zu erhalten, die wir haben Gut Kann benutzen. Siehe unten: 5(3x-1) + x((2x)/(2)) + 8 - 3x 15x - 5 + x(x) + 8 - 3x 15x - 5 + x + 8 - 3x. bestehen jetzt da die einzigen verbleibenden Operationen Addition und Subtraktion sind, können wir die gleichen Terme kombinieren?. x + (15x - 3x) + (8 - 5) x + 12x + 3 

Faktorisieren wir unsere Gleichung mit dem größten gemeinsamen Teiler, 3. Dazu teilen wir jeden Term durch 3. 9x/3 = 3x 27x/3 = 9x -3/3 = -1 Der neue Ausdruck ist also 3x + 9x - 1. 
Für unseren Beispielausdruck 3x + 9x - 1 setzen wir den Ausdruck in Klammern und multiplizieren diesen Term mit dem größten gemeinsamen Teiler der umzuwandelnden Originalgleichung 3(3x + 9x - 1) bekommen. Diese Gleichung entspricht dem Original, 9x + 27x - 3. 
Angenommen, unser ursprünglicher Beispielausdruck 9x + 27x - 3 ist gleich dem Zähler eines größeren Bruchs mit 3 als Nenner. Dieser Bruch sieht so aus: (9x + 27x - 3)/3. Wir können die Faktorisierung verwenden, um diesen Bruch zu vereinfachen. Addiere die faktorisierte Form unseres ursprünglichen Ausdrucks zum Zähler: (3(3x + 9x - 1))/3 Beachten Sie, dass sowohl Zähler als auch Nenner 3 als Koeffizienten haben. Wenn Sie Zähler und Nenner durch 3 teilen, erhalten Sie: (3x + 9x - 1)/1. Denn ein Bruch mit "1" im Nenner gleich den Termen im Zähler ist, können wir sagen, dass unser ursprünglicher Bruch vereinfacht werden kann zu 3x + 9x - 1. 

Nehmen wir ein einfaches Beispiel - √(90). Wenn wir die Zahl 90 als Produkt der beiden Faktoren 9 und 10 nehmen, können wir die Quadratwurzel von 9 berechnen, um 3 zu erhalten, und sie vor das Radikal setzen. Mit anderen Worten: (90) (9×10) (√(9) × √(10)) 3 × (10) 3√(10) 
Angenommen, wir haben den Ausdruck 6x × 8x + (x/x). In allen Fällen, in denen Exponenten multipliziert oder dividiert werden müssen, subtrahieren bzw. addieren wir die Exponenten, um einen vereinfachten Term schnell zu lösen. Siehe unten: 6x × 8x + (x/x) (6×8)x + (x) 48x + x Eine Erklärung finden Sie unten: Das Multiplizieren von Exponentialtermen ist im Wesentlichen dasselbe wie das Multiplizieren langer Reihen von Termen ohne Exponenten. Zum Beispiel, weil x = x × x × x und x= x × x × x × x × x, x × x = (x × x × x) × (x × x × x × x × x) oder x. Ebenso ist das Teilen von Exponentialtermen dasselbe wie das Teilen langer Folgen von Termen ohne Exponenten. x/x = (x × x × x × x × x)/(x × x × x). Da jeder Term im Zähler gegen den gleichen Term im Nenner annulliert werden kann, bleibt uns zweimal ein x im Zähler und keines im Nenner, so dass wir als Antwort x übrig haben.
Vereinfachung mathematischer gleichungen
Die Fähigkeit, algebraische Gleichungen zu vereinfachen, ist ein wesentlicher Bestandteil der Beherrschung der Grundlagen der Algebra und ein äußerst wertvolles Werkzeug für alle Mathematiker. Die Vereinfachung ermöglicht es einem Mathematiker, einen komplexen, langen und/oder ungeschickten Ausdruck in eine einfachere oder bequemere, aber äquivalente Form zu ändern. Die Grundlagen des Vereinfachens sind ziemlich einfach zu erlernen - sogar für jemanden, der Mathe hasst. Mit wenigen einfachen Schritten ist es möglich, viele der gebräuchlichsten algebraischen Ausdrücke ohne besondere mathematische Kenntnisse zu vereinfachen.
Schritte
Methode 1 von 4: Schlüsselkonzepte verstehen

1. Bestimmen "Augenhöhe" nach ihren Variablen und Potenzen. In Algebra besitzen "Augenhöhe" über die gleichen Variablen, potenziert mit der gleichen Potenz. Mit anderen Worten, zwei Begriffe sind "ähnlich", wenn sie die gleiche(n) Variable(n) oder gar keine haben, und wenn jede Variable die gleiche Potenz hat oder keine. Die Reihenfolge der Variablen innerhalb eines Termes spielt keine Rolle.
- Zum Beispiel sind 3x und 4x gleiche Terme, weil jeder Term eine Variable x hat, die in die zweite Potenz erhoben wird. Die Variablen x und x sind nicht gleich Terme, da x in jedem Term eine andere Potenz hat. Ebenso sind -3yx und 5xz keine gleichen Terme, da jeder Term aus unterschiedlichen Variablen besteht.

2. Faktorisieren Sie, indem Sie die Zahlen als das Produkt zweier Faktoren schreiben. Die Faktorisierung ist eine Methode, eine gegebene Zahl als das Produkt zweier Faktoren zu schreiben. Zahlen können aus mehreren Faktoren bestehen – zum Beispiel die Zahl 12, die aus 1 × 12, 2 × 6 und 3 × 4 gebildet werden kann, sodass wir sagen können, dass 1, 2, 3, 4, 6, und 12 sind alle Faktoren von 12. Eine andere Sichtweise ist, dass die Faktoren einer Zahl die Zahlen sind, durch die sie teilbar ist.

3. Verwenden Sie die Mnemonik „How Should We Get Rid Of The Inadequacies“ (oder als Akronym HMWVDOA), um sich die Reihenfolge der Operationen zu merken. Manchmal führt das Vereinfachen eines Ausdrucks nur dazu, die Operationen im Ausdruck auszuführen, bis nichts mehr getan werden kann. In diesem Fall ist es wichtig, die Reihenfolge der Operationen zu kennen, um Rechenfehler zu vermeiden. Diese Gedächtnisstütze kann Ihnen dabei helfen, sich die Reihenfolge der Bearbeitungen zu merken – die Buchstaben entsprechen der Art der Bearbeitungen, die Sie durchführen müssen und in welcher Reihenfolge. Wenn das gleiche Problem Multiplikationen und Divisionen enthält, müssen Sie diese Operationen von links nach rechts ausführen, wenn Sie an diesem Punkt angelangt sind. Das gleiche gilt für Addition und Subtraktion. Das obige Bild gibt eine Antwort, die nicht richtig ist. Der letzte Schritt hat die Addition und Subtraktion von links nach rechts nicht geklappt. Zuerst wurde es hinzugefügt. Es sollte 25 - 20 = 5 sein und dann 5 + 6 = 11.
Methode 2 von 4: Ähnliche Begriffe kombinieren

1. Schreibe deine Gleichungen auf. Die einfachsten mathematischen Gleichungen (solche mit nur wenigen Variablen und Koeffizienten als ganze Zahlen, ohne Brüche, Quadratwurzeln usw.) lässt sich oft in wenigen Schritten lösen. Wie bei den meisten mathematischen Problemen besteht der erste Schritt zur Vereinfachung einer Gleichung darin, die Gleichung zu schreiben!
- Für die nächsten Schritte verwenden wir den Ausdruck 1 + 2x - 3 + 4x als Beispiel.

2. Bestimmen Sie, was die gleichen Begriffe sind. Suchen Sie nun nach den gleichen Termen in Ihrer Gleichung. Denken Sie daran, dass gleiche Terme beide die gleichen Variablen und Exponenten haben.

3. Kombiniere ähnliche Begriffe. Nachdem Sie nun die gleichen Terme bestimmt haben, können Sie sie kombinieren, um Ihre Gleichung zu vereinfachen. Addiere Terme zusammen (oder subtrahiere sie bei negativen Termen), um jeden Satz von Termen (mit denselben Variablen und Exponenten) zu einem Term zu vereinfachen.

4. Machen Sie einen vereinfachten Ausdruck Ihrer vereinfachten Begriffe. Nachdem Sie Ihre ähnlichen Begriffe kombiniert haben, erstellen Sie einen Ausdruck aus Ihrem neuen, kleineren Satz von Begriffen. Sie sollten jetzt einen einfacheren Ausdruck mit einem Term für jeden Satz von Variablen und Exponenten im ursprünglichen Ausdruck haben. Dieser neue Ausdruck entspricht dem ersten.

5. Halten Sie die Reihenfolge der Operationen ein, wenn Sie ähnliche Terme kombinieren. In sehr einfachen Ausdrücken wie den, die wir in den obigen Übungen behandelt haben, ist es einfach, die gleichen Begriffe zu erkennen. Bei komplexeren Ausdrücken, wie etwa solchen mit Termen in Klammern, Brüchen und Wurzeln, ist das Kombinieren gleicher Terme nicht sofort offensichtlich. Befolgen Sie in diesen Fällen die Reihenfolge der Operationen und führen Sie die Operationen mit den Termen in Ihrem Ausdruck aus, bis nur noch Addition und Subtraktion übrig sind.
Methode 3 von 4: Factoring

1. Finden Sie den größten gemeinsamen Teiler im Ausdruck. Faktorisieren ist eine Möglichkeit, Ausdrücke zu vereinfachen, indem Faktoren entfernt werden, die in allen Ausdrücken des Ausdrucks vorkommen. Finden Sie zunächst den größten gemeinsamen Teiler aller Terme im Ausdruck – mit anderen Worten die größte Zahl, durch die alle Terme im Ausdruck teilbar sind.
- Angenommen, wir nehmen die Gleichung 9x + 27x - 3. Beachten Sie, dass jeder Term in dieser Gleichung durch 3 . teilbar ist. Denn Nein der Terme vollständig durch eine andere, größere Zahl teilbar ist, können wir sagen, dass 3 ist der größte gemeinsame Nenner unseres Ausdrucks.

2. Teile die Terme im Ausdruck durch den größten gemeinsamen Teiler. Dann dividiere jeden Term in deiner Gleichung durch den größten gemeinsamen Teiler, den du gerade gefunden hast. Die resultierenden Terme haben alle kleinere Koeffizienten als die im ursprünglichen Ausdruck.

3. Schreiben Sie Ihren Ausdruck als Produkt des größten gemeinsamen Teilers und der restlichen Terme. Ihr neuer Ausdruck ist nicht derselbe wie der alte, daher ist es nicht richtig zu sagen, dass es sich um die vereinfachte Version handelt. Um den neuen Ausdruck dem alten gleichzusetzen, müssen wir berücksichtigen, dass er durch den größten gemeinsamen Teiler geteilt wird. Setzen Sie Ihren neuen Ausdruck in Klammern und schreiben Sie den größten gemeinsamen Teiler der ursprünglichen Gleichung als Koeffizienten des Ausdrucks ebenfalls in Klammern.

4. Faktor zum Vereinfachen von Brüchen. Sie fragen sich jetzt vielleicht, warum die Faktorisierung sinnvoll ist, wenn der neue Ausdruck nach Entfernen des größten gemeinsamen Teilers erneut multipliziert werden muss. Die Faktorisierung ermöglicht es einem Mathematiker, eine Reihe von Tricks anzuwenden, um einen Ausdruck zu vereinfachen. Einer der einfachsten dieser Tricks nutzt die Tatsache, dass die Multiplikation von Zähler und Nenner eines Bruchs mit derselben Zahl einen Bruch im gleichen Verhältnis ergibt. Siehe unten:
Methode 4 von 4: Vereinfachen anwenden

1. Vereinfachen Sie Brüche, indem Sie durch gleiche Faktoren dividieren. Wenn Zähler und Nenner eines Ausdrucks die gleichen Faktoren haben, wie oben erwähnt, können diese Faktoren aus dem Bruch entfernt werden. Manchmal erfordert dies, dass der Zähler, Nenner oder beide faktorisiert werden (wie im obigen Beispiel), während in anderen Fällen die gemeinsamen Faktoren sofort ersichtlich sind. Beachten Sie, dass es auch möglich ist, die einzelnen Terme im Zähler durch den Ausdruck im Nenner zu dividieren, um einen vereinfachten Ausdruck zu erhalten.
- Lassen Sie uns ein Beispiel angehen, bei dem Sie sie nicht unbedingt aufschreiben müssen, um es zu vereinfachen. Angenommen, Sie haben den Bruch (5x + 10x + 20)/10, Sie können jeden Term im Zähler durch die 10 im Nenner dividieren, um das Ganze zu vereinfachen, auch wenn die "5" in 5x nicht größer als 10 und es ist nicht möglich, 10 als Faktor zu wählen.
- Dadurch erhalten wir ((5x)/10) + x + 2. Wenn wir wollen, können wir den ersten Term in (1/2)x umschreiben, um (1/2)x + x + 2 . zu erhalten.

2. Verwenden Sie Quadratwurzeln, um Wurzeln zu vereinfachen. Ausdrücke unter dem Vorzeichen einer Quadratwurzel heißen Quadratwurzelgleichungen. Sie können dies vereinfachen, indem Sie die Quadratwurzeln (Faktoren, die selbst eine zweite Potenz einer ganzen Zahl bilden) bestimmen und dann die Quadratwurzel dieser Faktoren abziehen, um sie aus dem Wurzelzeichen zu entfernen.

3. Addiere die Exponenten, wenn du zwei Exponentialterme multipliziert, und subtrahiere sie, wenn du dividierst. Einige algebraische Gleichungen erfordern das Multiplizieren oder Dividieren von Exponentialtermen. Sie berechnen nicht jeden Exponentialterm und multiplizieren oder dividieren nicht manuell, aber zählen Sie addieren die Exponenten jedes Termes, wenn Sie sie miteinander multiplizieren und ziehst du sie Wenn Sie sie teilen, sparen Sie viel Zeit. Sie können dieses Konzept auch anwenden, um Gleichungen mit mehreren Variablen zu vereinfachen.
Tipps
- Denken Sie daran, dass Sie diese Zahlen als positiv oder negativ betrachten müssen. Viele Leute bleiben dabei stecken und denken nach, "Welches Zeichen soll ich hier setzen?"
- Bitte um Hilfe, wenn du sie brauchst!
- Es ist nicht einfach, mathematische Gleichungen zu vereinfachen, aber wenn du einmal den Dreh raus hast, kannst du es für den Rest deines Lebens verwenden.
Warnungen
- Passen Sie auf, dass Sie nicht versehentlich zusätzliche Zahlen, Exponenten oder Operationen hinzufügen, die nicht dorthin gehören.
- Achtet immer auf Gleichberechtigung und lasst euch nicht von den Exponenten täuschen.
"Vereinfachung mathematischer gleichungen"
Оцените, пожалуйста статью