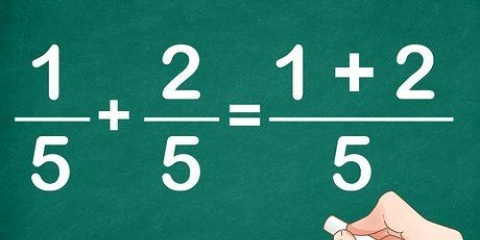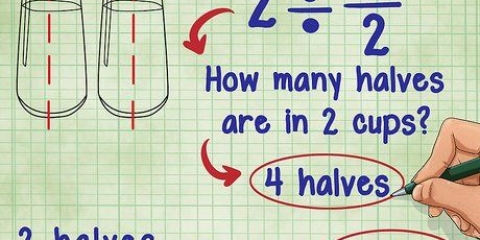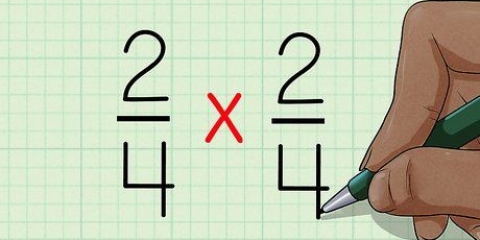Brüche vereinfachen

Schritte
Tipps

Mathematik muss nicht schwer sein, aber es ist nicht immer einfach, sich all die verschiedenen Prinzipien und Methoden zu merken. Sogar die Grundtechniken können manchmal vergessen werden. Also, hier sind zwei weitere Methoden, um Brüche zu vereinfachen.

Schritte

Methode 1 von 4: Den größten gemeinsamen Teiler verwenden

1. Listen Sie alle Faktoren des Zählers und Nenners auf. Die Faktoren einer gegebenen Zahl sind die Zahlen, die zusammen diese Zahl ergeben. Beispiel, 3 und 4 sind beide Faktoren von 12, weil 3 x 4 = 12. Um alle Faktoren einer Zahl aufzulisten, finde heraus, welche Zahlen alle bis in diese Zahl passen.

Listen Sie die Faktoren vom kleinsten bis zum größten auf und vergessen Sie nicht die 1. Dies ist die Liste:

24: 1, 2, 3, 4, 6, 8, 12, 24.
32: 1, 2, 4, 8, 16, 32.

2. Finden Sie den größten gemeinsamen Teiler (gcd) von Zähler und Nenner. Die gcd ist die größte Zahl, durch die zwei Zahlen, in diesem Fall der Zähler und der Nenner, teilbar sind. Sobald Sie die beiden Listen mit Faktoren erstellt haben, müssen Sie nur noch die größte Zahl (den Divisor) finden, die in beiden Listen vorkommt.

24: 1, 2, 3, 4, 6, 8, 12, 24.

32: 1, 2, 4, 8, 16, 32.

Die gcd von 24 und 32 ist 8, weil 8 die größte Zahl ist, durch die sowohl 24 als auch 32 teilbar sind.

3. Teilen Sie Zähler und Nenner durch die gcd. Nachdem Sie nun den gcd gefunden haben, müssen Sie nur noch Zähler und Nenner durch diese Zahl dividieren, um Ihren Bruch so weit wie möglich zu vereinfachen. So funktioniert das:

24/8 = 3

32/8 = 4

Der vereinfachte Bruch ist also 3/4.

4. Überprüfe deine Arbeit. Wenn Sie wissen möchten, ob Ihre Vereinfachung richtig ist, multiplizieren Sie den Zähler und den Nenner der Vereinfachung mit dem gcd, um sicherzustellen, dass Sie als Ergebnis den ursprünglichen Bruch zurückerhalten. So funktioniert das:

3 * 8 = 24

4 * 8 = 32

Dies ist wieder der ursprüngliche Bruch, 24/32.

Sie können auch untersuchen, ob der Bruch nicht noch weiter vereinfacht werden kann. Da 3 eine Primzahl ist, kann sie nur durch 1 und sich selbst geteilt werden, sodass dieser Bruch nicht weiter vereinfacht werden kann.

Methode 2 von 4: Teilen Sie weiter durch eine kleine Zahl

1. Wähle eine kleine Zahl. Wählen Sie bei dieser Methode einfach eine kleine Zahl aus, z. B. 2, 3, 4, 5 oder 7, um zu beginnen. Schauen Sie sich die Brüche an, um sicherzustellen, dass die Zahl mindestens einmal durch eine beliebige Zahl teilbar ist. Wenn du zum Beispiel den Bruch 24/108 nimmst, wähle keine 5 aus, weil sie zu keiner der Zahlen passt. Aber wenn Sie den Bruch 25/60 untersuchen, dann ist 5 eine gute Wahl.

Bei der Fraktion 24/32 funktioniert die Zahl 2 super. Da beide Zahlen gerade sind, sind sie auch durch 2 . teilbar.

2. Dividiere den Zähler und Nenner eines Bruchs durch diese Zahl, um ihn zu vereinfachen. So hat es geklappt:

24/2 = 12

32/2 = 16

Der neue, vereinfachte Bruch ist 12/16.

3. wiederholen Sie dies. Da beide Zahlen immer noch gerade sind, können Sie weiter durch 2 . dividieren. Wenn eine der Zahlen ungerade wird, versuchen Sie es mit einer anderen Zahl als Teiler. So geht das weiter:

12/2 = 6

16/2 = 8

Der neue Bruch ist 6/8.

4. Teile so lange durch 2, bis du nicht mehr weiterkommst.

6/2 = 3

8/2 = 4

Der neue Bruch ist 3/4.

5. Stellen Sie sicher, dass der Bruch nicht weiter vereinfacht werden kann. Wie im vorherigen Beispiel: 3 ist eine Primzahl und daher kann ¾ nicht weiter vereinfacht werden. Wenn Zähler und Nenner eines Bruchs nicht erneut durch die gewählte Zahl geteilt werden können, versuchen Sie es mit einer anderen Zahl.

Wenn Sie beispielsweise den Bruch 10/40 vereinfachen möchten, teilen Sie zunächst Zähler und Nenner durch 5, sodass 2/8 . übrig bleibt. Sie können nicht wieder durch 5 teilen, aber Sie können durch 2 teilen, wodurch die endgültige Antwort ¼ . wird.

6. Überprüfe deine Antwort. Arbeite dich zurück zum Ausgangspunkt, indem du 3/4 mit 2/2 dreimal multiplizierst und überprüfe, ob das Ergebnis 24/32 . ist. Hier seht ihr das ausgearbeitet:

3/4 * 2/2 = 6/8

6/8 * 2/2 = 12/16

12/16 * 2/2 = 24/32.

Beachten Sie, dass Sie 24/32 durch 2 * 2 * 2 geteilt haben, was der Division durch 8 entspricht, dem größten gemeinsamen Teiler von 24 und 32.

Methode 3 von 4: Nennen Sie die Teiler

1. Schreibe deinen Bruch auf. Lassen Sie auf der rechten Seite Ihres Papiers viel Platz – es geht nur darum, die Faktoren aufzuschreiben.

2. Nenne die Faktoren des Zählers und Nenners. Setzen Sie sie in separate Listen. Es könnte einfacher sein, wenn die Listen übereinander ausgerichtet sind. Beginne mit 1 und gehe dann vom kleinsten zum größten und schreibe die Paare auf.

Zum Beispiel: Wir haben den Bruch 24/60. Beginnen Sie mit 24.Sie merken: 24 -- 1, 2, 3, 4, 6, 8, 12, 24

Dann weiter mit 60.Sie merken: 60 -- 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60

3. Finden Sie den größten gemeinsamen Teiler (gcd).Was ist die größte Zahl, die sowohl ein Teiler des Zählers als auch des Nenners ist?? Was auch immer es ist, dividiere beide Zahlen durch diese Zahl.

In unserem Beispiel ist die größte Zahl der Teiler 12. Also dividieren wir beide 24 und 60 durch 12, was den Bruch 2/5 ergibt – unser vereinfachter Bruch!

Methode 4 von 4: Verwenden von Primfaktoren

1. Finden Sie die Primfaktoren von Zähler und Nenner. EIN "Primzahl" ist eine Zahl, die durch keine andere ganze Zahl außer 1 und sich selbst geteilt werden kann. 2, 3, 5, 7 und 11 sind Beispiele für Primzahlen.

Beginnen Sie mit der Theke. Teilen Sie 24 in die Faktoren 2 und 12. weil 2 eine Primzahl ist, sind Sie sofort mit diesem Zweig fertig! Unterteile nun 12 in die Faktoren 2 und 6. 2 ist prim – gut! Teilen Sie nun die 6 in die Faktoren 2 und 3. Jetzt hast du 2, 2, 2 und 3 als Primzahlen.
Weiter mit dem Nenner. Teilen Sie 60 in die Faktoren 2 und 30. Teilen Sie 30 in die Faktoren 2 und 15. Teile 15 in 3 und 5, beide Primzahlen. Jetzt haben Sie die folgende Liste von Primzahlen: 2, 2, 3 und 5.

2. Schreibe die Primfaktoren von Zähler und Nenner auf. Nimm die Reihe der Primzahlen, die du gefunden hast, multipliziere sie miteinander. Tun Sie dies für Zähler und Nenner. So kann man leichter sehen, was passiert.

Für 24 hast du also 2 x 2 x 2 x 3 = 24.

Und für 60 hast du 2 x 2 x 3 x 5 = 60

3. Ignoriere die gleichen Faktoren. Jedes Zahlenpaar aus einer der beiden Serien kann entfernt werden. In diesem Fall haben wir zwei Zweierpaare und ein Dreierpaar. Diese können entfernt werden!

Was uns bleibt sind eine 2 und eine 5 – oder 2/5! Die gleiche Antwort haben wir mit der vorherigen Methode erhalten.

Wenn Zähler und Nenner gerade Zahlen sind, denken Sie daran, die Zahl in zwei Hälften zu teilen. Mach so weiter, bis sie zu klein sind, um sich weiter aufzuspalten.