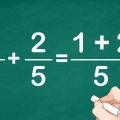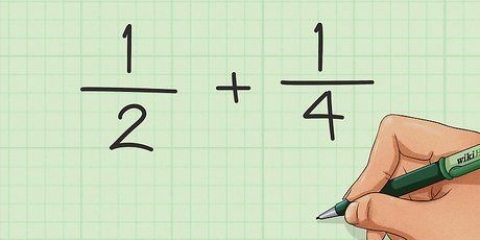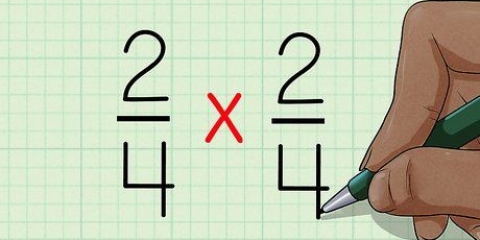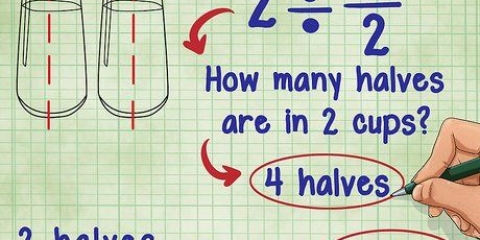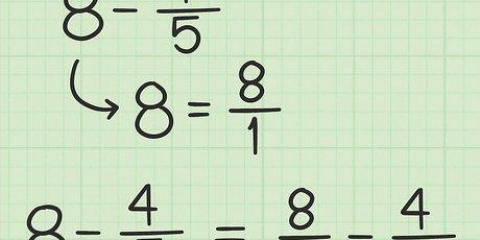Brüche lösen

Schritte
Tipps
Warnungen

Brüche scheinen manchmal etwas schwierig zu lösen, aber mit ein wenig Übung und etwas Zusatzwissen wird dies viel einfacher. Sobald Sie die Grundlagen verstanden haben, werden Sie feststellen, dass das Lösen von Brüchen eigentlich ein Kinderspiel ist.

Schritte

Methode 1 von 4: Brüche multiplizieren

Bildtitel Lösen Sie Bruchfragen in Math Step 1

1. Stellen Sie sicher, dass Sie es mit zwei Brüchen zu tun haben. Diese Anleitung funktioniert nur mit zwei Brüchen.Wenn es sich um einen gemischten Bruch handelt, wandeln Sie ihn zuerst in einen unechten Bruch um...

Bildtitel Lösen von Fraction Questions in Math Step 2

2. Multipliziere Zähler 1 mit Zähler 2 und multipliziere Nenner 1 mit Nenner 2.

Angenommen, wir haben 1/2 x 3/4, dann multiplizieren wir wie folgt: 1 x 3 und 2 x 4.Die Antwort ist dann 3/8.

Methode 2 von 4: Brüche teilen

Bildtitel Lösen von Fraction Questions in Math Step 3

1. Stellen Sie sicher, dass Sie es mit zwei Brüchen zu tun haben. Auch dieser Vorgang funktioniert NUR, wenn Sie gemischte Brüche in unechte Brüche umgewandelt haben.

Bildtitel Lösen von Fraction Questions in Math Step 4

2. Kehre den zweiten Bruch um. Es ist egal welcher Bruch, solange Sie nicht beide Brüche umkehren.

Bildtitel Lösen Sie Bruchfragen in Math Step 5

3. Ändere das Divisionszeichen in eine Multiplikation.

Wenn das Problem 8/15 ÷ 3/4 war, ist dies jetzt 8/15 x 4/3.

Bildtitel Lösen von Fraction Questions in Math Step 6

4. Beide Zähler und beide Nenner multiplizieren.

8 x 4 = 32 und 15 x 3 = 45, die Antwort lautet also 32/45.

Methode 3 von 4: Umwandeln gemischter Brüche in unechte Brüche

Bildtitel Lösen von Bruchfragen in Math Step 7

1. Wandeln Sie gemischte Brüche in unechte Brüche um. Unechte Brüche sind Brüche, deren Zähler größer ist als der Nenner.(Zum Beispiel 17/5.)Wenn Sie multiplizieren und dividieren, müssen Sie gemischte Brüche in unechte Brüche umwandeln, bevor Sie das Problem weiter lösen.

Angenommen, Sie haben den gemischten Bruch 3 2/5.

Bildtitel Lösen von Bruchfragen in Math Step 8

2. Nimm die ganze Zahl (die Zahl vor dem Bruch) und multipliziere sie mit dem Nenner.

In unserem Beispiel wird daraus: 3 x 5 = 15.

Bildtitel Lösen von Bruchfragen in Math Step 9

3. Füge diese Antwort dem Zähler hinzu.

In unserem Beispiel: 15 + 2 = 17

Bildtitel Lösen von Fraction Questions in Math Step 10

4. Platziere diese Zahl als neuen Zähler über der Bruchlinie und du hast einen unechten Bruch.

In unserem Fall wird dies: 17/5.

Methode 4 von 4: Brüche addieren und subtrahieren

Bildtitel Lösen von Fraction Questions in Math Step 11

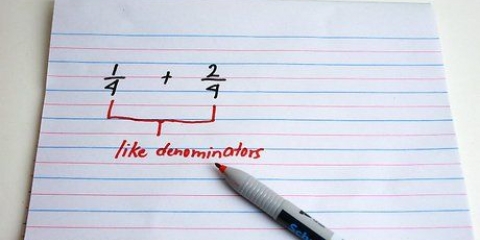
1. Finden Sie das kleinste gemeinsame Vielfache der Nenner (die untere Zahl). Sowohl beim Addieren als auch beim Subtrahieren von Brüchen beginnen Sie mit dem gleichen. Finde die kleinste Zahl, die auf beide Nenner passt.

Wenn Sie beispielsweise die Brüche 1/4 und 1/6 nehmen, ist das kleinste gemeinsame Vielfache 12. (4x3=12, 6x2=12)

Bildtitel Lösen von Bruchfragen in Math Step 12

2. Multipliziere die Brüche in Abhängigkeit vom kleinsten gemeinsamen Vielfachen. Denken Sie daran, Sie ändern nicht den Bruch, sondern nur, wie er ausgedrückt wird. Stellen Sie sich eine Pizza vor - 1/2 oder 2/4 einer Pizza sind gleich viel Pizza, nur anders ausgedrückt.

Bestimme, wie oft der gegenwärtige Nenner in das kleinste gemeinsame Vielfache eingeht. Für 1/4, 4 x 3 = 12. Für 1/6, 6 x 2 = 12.

Zähler und Nenner des Bruchs mit dieser Zahl multipliziert. Für ¼ multiplizieren Sie sowohl 1 als auch 4 mit 3, was 3/12 . ergibt. 1/6 x 2 = 2/12. Nun sieht diese Aussage so aus: 3/12 + 2/12 oder 3/12 - 2/12.

Bildtitel Lösen von Bruchfragen in Math Step 13

3. Addiere oder subtrahiere die beiden Zähler (obere Zahl), aber NICHT die Nenner.Dies ist nicht erlaubt, da Sie berechnen möchten, wie viel von diesem Anteil Sie insgesamt haben. Wenn Sie auch die Nenner mit einbeziehen, ändern sich die Brüche.

Für 3/12 + 2/12 lautet die Antwort also 5/12. Für 3/12 - 2/12 ist es 1/12

Tipps

Achte darauf, dass du die mathematischen Grundkenntnisse (Addition, Subtraktion, Multiplikation und Division) gut beherrschst, damit die Berechnungen nicht unnötig lange dauern und schwierig werden.
Der Kehrwert einer ganzen Zahl setzt diese Zahl als Nenner in einen Bruch, mit einer 1 als Zähler. Aus 5 wird dann beispielsweise 1/5.
Sie können gemischte Brüche multiplizieren und dividieren, ohne sie zuerst in unechte Brüche umzuwandeln. Aber dann braucht man andere mathematische Fähigkeiten, und die Berechnung wird viel komplexer. Daher ist es im Allgemeinen besser, dem Weg der unechten Brüche zu folgen.
Denken Sie daran: Dividieren ist dasselbe wie Multiplizieren mit dem Kehrwert.
Wenn Sie die Umkehrung einer negativen Zahl nehmen, bleibt das Minuszeichen im Zähler.