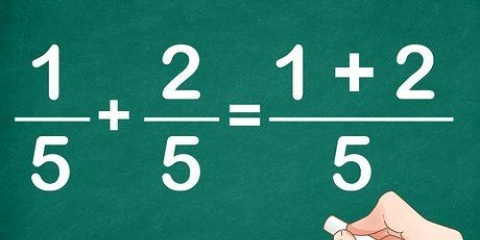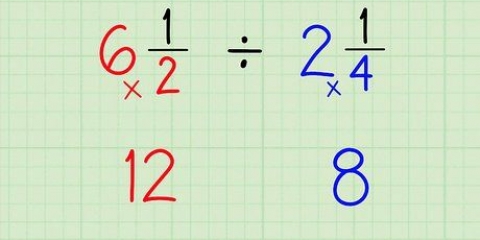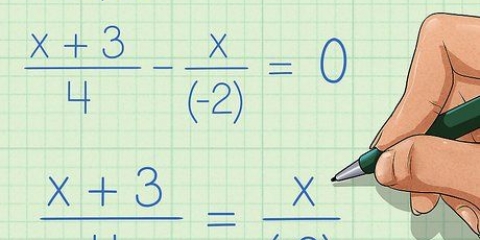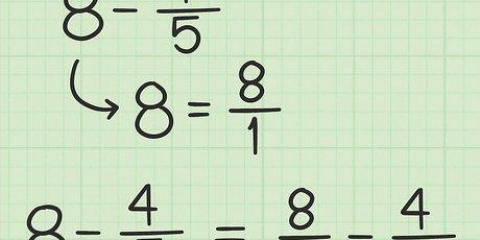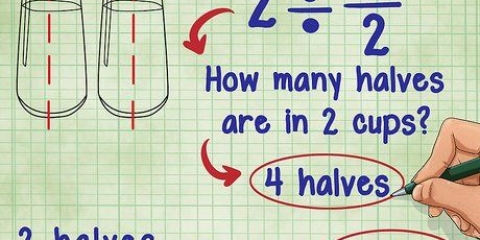Äquivalente Brüche auflösen: 8 Schritte (mit Bildern)

Schritte
- Methode 1 von 2: Erstellen äquivalenter Brüche
- Methode 2 von 2: Äquivalente Brüche mit Variablen lösen
Tipps
Warnungen

Zwei Brüche sind "Äquivalent" wenn sie den gleichen Wert haben. Zum Beispiel sind die Brüche 1/2 und 2/4 äquivalent, weil 1 über 2 den gleichen Wert hat wie 2 über 4 (0,5 in Dezimalform). Zu wissen, wie man einen Bruch in einen anderen, aber äquivalenten Bruch umwandelt, ist ein wesentlicher mathematischer Wert, den Sie benötigen, von der grundlegenden Algebra bis zur fortgeschrittenen Mathematik. Sehen Sie sich Schritt 1 an, um zu beginnen!

Schritte

Methode 1 von 2: Erstellen äquivalenter Brüche

Bildtitel Do Equivalent Fractions Step 1

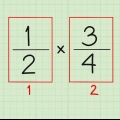
1. Multipliziere Zähler und Nenner eines Bruchs mit derselben Zahl, um einen äquivalenten Bruch zu erhalten. Zwei Brüche, die unterschiedlich sind, aber per Definition äquivalent sind, Zähler und Nenner, die Vielfache voneinander sind. Mit anderen Worten, die Multiplikation von Zähler und Nenner eines Bruchs mit derselben Zahl ergibt einen äquivalenten Bruch. Auch wenn die Zahlen in diesem neuen Bruch unterschiedlich sind, hat er immer noch den gleichen Wert.

Wenn wir zum Beispiel den Bruch 4/8 nehmen und Zähler und Nenner mit 2 multiplizieren, erhalten wir (4×2)/(8×2) = 8/16. Diese beiden Brüche sind äquivalent.

(4×2)/(8×2) ist im Wesentlichen dasselbe wie 4/8 × 2/2. Denken Sie daran, wenn wir zwei Brüche multiplizieren, machen wir es so - Zähler mal Zähler und Nenner mal Nenner. Beachten Sie, dass 2/2 gleich 1 . ist. Es ist also leicht zu erkennen, warum 4/8 gleich 8/16 ist - der zweite Bruch ist der erste Bruch multipliziert mit 2!

2. Dividiere Zähler und Nenner oder einen Bruch durch dieselbe Zahl, um einen äquivalenten Bruch zu erhalten. Wie bei der Multiplikation kann auch die Division verwendet werden, um einen neuen Bruch zu erzeugen, der dem gegebenen Bruch entspricht. Teilen Sie einfach Zähler und Nenner eines Bruchs durch dieselbe Zahl, um einen äquivalenten Bruch zu erhalten. Hier gibt es eine Einschränkung – der resultierende Bruch muss sowohl im Zähler als auch im Nenner aus ganzen Zahlen bestehen, um gültig zu sein.

Nehmen wir zum Beispiel wieder 4/8. Wenn wir, anstatt zu multiplizieren, sowohl den Zähler als auch den Nenner durch 2 teilen, erhalten wir (4 2)/(8 ÷ 2) = 2/4. 2 und 4 sind beide ganze Zahlen, also ist dieser äquivalente Bruch gültig.

Bildtitel Do Equivalent Fractions Step 2

3. Vereinfachen Sie Ihren Bruch mit dem größten gemeinsamen Teiler (GGD). Jeder gegebene Bruch hat unendlich viele äquivalente Brüche - Sie können den Zähler und Nenner mit multiplizieren jede ganze Zahl, groß oder klein um einen äquivalenten Bruch zu erhalten. Aber die einfachste Form eines gegebenen Bruchs ist normalerweise die mit den kleinsten Termen. In diesem Fall sind Zähler und Nenner beide so klein wie möglich - sie können nicht mehr durch eine ganze Zahl geteilt werden, um den Term noch kleiner zu machen. Um einen Bruch zu vereinfachen, dividieren wir Zähler und Nenner durch größter gemeinsamer Teiler.

Der größte gemeinsame Teiler (GGD) von Zähler und Nenner ist die größte ganze Zahl, durch die Zähler und Nenner teilbar sind. Also in unserem 4/8 Beispiel, weil 4 der größte Teiler von 4 und 8 ist, dividieren wir Zähler und Nenner unseres Bruchs durch 4, um die einfachsten Terme zu erhalten. (4 4)/(8 ÷ 4) = 1/2.

Bildtitel Do Equivalent Fractions Step 8

4. Wandeln Sie bei Bedarf gemischte Zahlen in unechte Brüche um, um die Umrechnung zu erleichtern. Natürlich lässt sich nicht jeder Bruch, auf den Sie stoßen, so einfach wie 4/8 . vereinfachen. Zum Beispiel gemischte Zahlen (zB. 1 3/4, 2 5/8, 5 2/3 usw.) kann diese Konvertierung etwas erschweren. Wenn Sie einen Bruch einer gemischten Zahl bilden möchten, können Sie dies auf zwei Arten tun: Machen Sie die gemischte Zahl zu einem unechten Bruch und fahren Sie dann fort, oder Behalte die gemischte Zahl und gib eine gemischte Zahl als Antwort an.

Um einen unechten Bruch umzuwandeln, multiplizieren Sie die ganze Zahl der gemischten Zahl mit dem Nenner des Bruchs und addieren Sie dann das Produkt zum Zähler. Beispiel: 1 2/3 = ((1 × 3) + 2)/3 = 5/3. Dann können Sie es bei Bedarf wieder konvertieren. Zum Beispiel 5/3 × 2/2 = 10/6, immer noch das gleiche wie 1 2/3.

Es ist jedoch nicht erforderlich, einen unechten Bruch umzuwandeln. Wir können die ganze Zahl ignorieren und einfach den Bruch umwandeln und dann die ganze Zahl dazu addieren. Zum Beispiel betrachten wir bei 3 4/16 nur 4/16. 4/16 4/4 = 1/4. Jetzt addieren wir die ganze Zahl wieder und erhalten eine neue gemischte Zahl, 3 1/4.

5. Addiere oder subtrahiere niemals, um äquivalente Brüche zu erhalten. Beim Umwandeln von Brüchen in ihre äquivalente Form ist es wichtig, sich daran zu erinnern, dass die einzigen Operationen, die Sie anwenden, Multiplikation und Division sind. Verwenden Sie niemals Addition oder Subtraktion. Multiplikation und Division funktionieren, um äquivalente Brüche zu erhalten, da diese Operationen tatsächlich Formen der Zahl 1 (2/2, 3/3 usw.) sind.)und gib Antworten, die dem Bruch entsprechen, mit dem du angefangen hast. Addition und Subtraktion haben diese Fähigkeit nicht.

Oben haben wir beispielsweise festgestellt, dass 4/8 ÷ 4/4 = 1/2 . Wenn wir stattdessen 4/4 hinzugefügt hätten, hätten wir eine ganz andere Antwort erhalten. 4/8 + 4/4 = 4/8 + 8/8 = 12/8 = 1 1/2 oder 3/2, und keines davon ist gleich 4/8.

Methode 2 von 2: Äquivalente Brüche mit Variablen lösen

1. Verwenden Sie die Kreuzmultiplikation, um Äquivalenzprobleme mit Brüchen zu lösen. Eine knifflige Art von Algebraproblem, das sich mit äquivalenten Brüchen befasst, beinhaltet Gleichungen mit zwei Brüchen, von denen einer oder beide eine Variable enthalten. In solchen Fällen wissen wir, dass diese Brüche äquivalent sind, weil sie die einzigen Terme auf beiden Seiten des Gleichheitszeichens einer Gleichung sind, aber es ist nicht immer offensichtlich, wie man nach der Variablen auflöst. Glücklicherweise können wir mit kreuzweise multiplizieren, diese Art von Problemen ohne Probleme lösen.

Kreuzmultiplikation ist genau das, wonach es sich anhört - Sie multiplizieren kreuzweise über das Gleichheitszeichen. Mit anderen Worten, Sie multiplizieren den Zähler des einen Bruchs mit dem Nenner des anderen Bruchs und umgekehrt. Dann löst du die Gleichung weiter.
Zum Beispiel haben wir die Gleichung 2/x = 10/13. Jetzt kreuzmultiplizieren: Multiplizieren Sie 2 mit 13 und 10 mit x und arbeiten Sie die Gleichung weiter aus:

2×13 = 26
10 × x = 10 x
10x = 26. Jetzt arbeiten wir die Gleichung weiter aus. x = 26/10 = 2.6

2. Verwenden Sie die Kreuzmultiplikation auf die gleiche Weise wie multivariate Gleichungen oder variable Ausdrücke. Eine der besten Eigenschaften der Kreuzmultiplikation ist, dass sie ziemlich gleich funktioniert, egal ob Sie es mit zwei einfachen oder komplexen Brüchen zu tun haben. Wenn beispielsweise beide Brüche Variablen enthalten, ändert sich nichts - Sie müssen diese Variablen nur loswerden. Ebenso, wenn die Zähler oder Nenner Ihrer Bruchvariablen Ausdrücke enthalten, einfach "weiter vermehren" indem Sie die Verteilungseigenschaft verwenden und wie gewohnt lösen.

Angenommen, wir haben die Gleichung ((x + 3)/2) = ((x + 1)/4). In diesem Fall lösen wir dies durch Kreuzmultiplikation:

(x + 3) × 4 = 4x + 12

(x + 1) × 2 = 2x + 2

2x + 2 = 4x + 12

2 = 2x + 12

-10 = 2x

-5 = x

3. Verwenden Sie Techniken zum Lösen von Polynomen. Kreuzmultiplikation funktioniert nicht stets ein Ergebnis, das Sie mit einfacher Algebra lösen können. Wenn Sie es mit variablen Termen zu tun haben, erhalten Sie als Ergebnis schnell eine quadratische Gleichung oder ein anderes Polynom. In solchen Fällen verwendet man zum Beispiel die Quadratur und/oder die Quadratformel.

Zum Beispiel nehmen wir die Gleichung ((x +1)/3) = (4/(2x - 2)). Erstes Kreuz multiplizieren:

(x + 1) × (2x - 2) = 2x + 2x -2x - 2 = 2x - 2

4×3 = 12

2x - 2 = 12. An dieser Stelle wollen wir dies in eine quadratische Gleichung (ax + bx + c = 0) umwandeln, indem wir von beiden Seiten 12 subtrahieren, was 2x - 14 = 0 . ergibt. Nun verwenden wir die Formel (x = (-b +/- √(b - 4ac))/2a), um den Wert von x zu ermitteln:

x = (-b +/- √(b - 4ac))/2a. In unserer Gleichung 2x - 14 = 0, a = 2, b = 0 und c = -14.

x = (-0 +/- √(0 - 4(2)(-14))))/2(2)

x = (+/- ( 0 - -112))/2(2)

x = (+/- (112))/2(2)

x = (+/- 10.58/4)

x = +/- 2.64 An dieser Stelle überprüfen wir unsere Antwort, indem wir 2,64 und -2,64 in die ursprüngliche quadratische Gleichung einsetzen.

Tipps

Das Umwandeln von Brüchen in eine äquivalente Form ist eigentlich wie das Multiplizieren mit einem Bruch wie 2/2 oder 5/5. Da diese letztendlich gleich 1 ist, bleibt der Wert des Bruchs gleich.