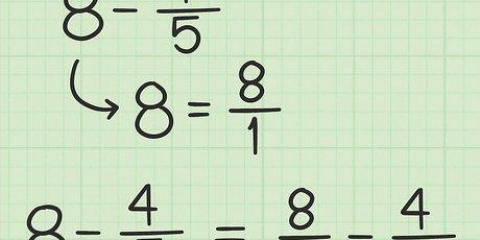Mathematische Brüche vereinfachen

Schritte
Tipps
Warnungen

Mathematische oder algebraische Brüche erscheinen zunächst unglaublich schwierig und können für den ungeübten Schüler entmutigend erscheinen. Bei einer Mischung aus Variablen, Zahlen und sogar Exponenten ist es schwer zu wissen, wo man anfangen soll. Aber zum Glück gelten die gleichen Regeln, die zur Vereinfachung üblicher Brüche wie 15/25 benötigt werden, auch für mathematische Brüche.

Schritte

Methode 1 von 3: Brüche vereinfachen

Bildtitel Simplify Algebraic Fractions Step 1

1. Kenne das Vokabular für mathematische Brüche. Die folgenden Begriffe werden in den Beispielen verwendet und sind bei Problemen mit Brüchen üblich:

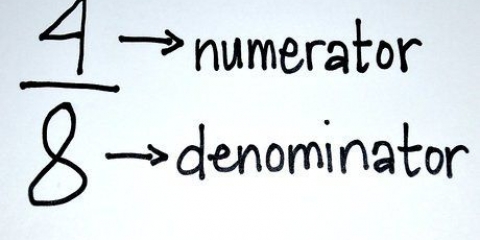
Zähler: Der obere Teil eines Bruchs (z.B. (x+5)/(2x+3)).
Nenner: Der untere Teil eines Bruchs (zB. (x+5)/(2x+3)).
Gemeinsamer Nenner: Dies ist eine Zahl, durch die Sie sowohl den Zähler als auch den Nenner eines Bruchs dividieren können. Zum Beispiel im Bruch 3/9 ist der gemeinsame Teiler 3, da beide Zahlen durch 3 . geteilt werden können.
Faktor:` Eine Zahl, die zu einer anderen Zahl multipliziert wird. Zum Beispiel: Die Faktoren von 15 sind 1, 3, 5 und 15. Die Faktoren von 4 sind 1, 2 und 4.
Vereinfachte Gleichung: Alle gemeinsamen Faktoren werden entfernt und gleiche Variablen werden gruppiert (5x + x = 6x), bis Sie die einfachste Form eines Bruchs, einer Gleichung oder eines Problems erhalten haben. Wenn du mit dem Bruch nichts mehr anfangen kannst, ist es vereinfacht.

Bildtitel Simplify Algebraic Fractions Step 2

2. Vergleichen Sie, wie man einfache Brüche löst. Dies sind genau die gleichen Schritte, die Sie ausführen werden, um mathematische Brüche zu lösen. Nehmen Sie das Beispiel, 15/35. Um einen Bruch zu vereinfachen, brauchen wir einen gemeinsamen Nenner finden. In diesem Fall können beide Zahlen durch fünf geteilt werden, sodass Sie die 5 aus dem Bruch streichen können:
fünfzehn→5 * 3
35→5 *7
Jetzt kannst du wie Begriffe durchstreichen. In diesem Fall können Sie die beiden Fünfen durchstreichen und Ihre vereinfachte Antwort hinterlassen, 3/7.

Bildtitel Simplify Algebraic Fractions Step 3

3. Entfernen Sie Faktoren aus algebraischen Ausdrücken wie normale Zahlen. Im vorherigen Beispiel könnten Sie die 5 leicht von 15 entfernen, und das gleiche Prinzip gilt für komplexere Ausdrücke wie 15x - 5. Finden Sie einen Faktor, den beide Zahlen gemeinsam haben. Hier ist die Antwort 5, weil Sie sowohl 15x als auch -5 durch die Zahl fünf teilen können. Wie zuvor entfernen Sie den gemeinsamen Faktor und multiplizieren ihn mit dem, was "verbleibend" ist.`
15x - 5 = 5 *(3x - 1) Um deine Arbeit zu überprüfen, multipliziere einfach die Fünf zurück in den neuen Ausdruck - du erhältst die gleichen Zahlen, mit denen du angefangen hast.

Bildtitel Simplify Algebraic Fractions Step 4

4. Jetzt können Sie komplexe Begriffe genauso wie einfache Begriffe löschen. Das gleiche Prinzip wie bei regulären Brüchen funktioniert auch für mathematische Brüche. Dies ist der einfachste Weg, Brüche zu vereinfachen. Nimm den Bruch:
(x+2)(x-3)
(x+2)(x+10)
Beachten Sie, wie der Begriff (x+2) sowohl im Zähler (oben) als auch im Nenner (unten) vorkommt. Daher können Sie diese entfernen, um den algebraischen Bruch zu vereinfachen, genau wie Sie die 5 aus 15/35 entfernt haben:
~~(x+2)~~(x-3)→(x-3)
~~(x+2)~~(x+10)→(x+10) Dies ergibt die endgültige Antwort: (x-3)/(x+10).

Methode 2 von 3: Brüche vereinfachen

Bildtitel Simplify Algebraic Fractions Step 5

1. Finden Sie einen gemeinsamen Faktor im Zähler (der obere Teil des Bruchs). Das erste, was Sie beim Vereinfachen eines algebraischen Bruchs tun müssen, ist, jeden Teil des Bruchs zu vereinfachen. Beginnen Sie mit dem oberen Teil und streichen Sie so viele Zahlen wie möglich durch. Als Beispiel verwenden wir diese Übung:
9x-3
15x+6
Beginnen Sie mit dem Zähler: 9x – 3. Es gibt einen gemeinsamen Faktor für 9x und -3, nämlich 3. Arbeiten Sie die 3 äußeren Klammern wie jede andere Zahl und lassen Sie 3*(3x-1) übrig. Das ist Ihr neuer Zähler:
3(3x-1)
15x+6

Bildtitel Simplify Algebraic Fractions Step 6

2. Finden Sie einen gemeinsamen Faktor im Nenner.Setzen Sie das Beispiel von oben fort und isolieren Sie den Nenner 15x+6. Suchen Sie erneut nach einer Nummer, die zu beiden Teilen passt. Auch hier kann man den Faktor drei weglassen, so dass man bei 3 bleibt *(5x +2). Bauen Sie Ihren neuen Nenner in die Gleichung ein:
3(3x-1)
3(5x+2)

Bildtitel Simplify Algebraic Fractions Step 7

3. Ähnliche Begriffe entfernen. Dies ist die Phase, in der Sie den Bruch wirklich vereinfachen können. Nimm alle Terme, die sowohl im Zähler als auch im Nenner vorkommen, und entferne sie. In diesem Fall können wir die 3 sowohl von oben als auch von unten durchstreichen.
3(3x-1)→(3x-1)
3(5x+2)→(5x+2)

Bildtitel Simplify Algebraic Fractions Step 8

4. Wissen, wann die Gleichung vollständig vereinfacht ist. Ein Bruch wird vereinfacht, wenn es oben oder unten keine gemeinsamen Faktoren mehr gibt. Denken Sie daran, dass Sie Faktoren innerhalb der Klammern nicht entfernen können - im Beispielproblem können Sie das x von 3x und 5x nicht faktorisieren, da die vollständigen Terme tatsächlich (3x -1) und (5x + 2) sind. Das Beispiel ist also völlig vereinfacht, mit if die letzte antwort:
(3x-1)
(5x+2)

Bildtitel Simplify Algebraic Fractions Step 9

5. Probieren Sie eine Übungsübung aus. Der beste Weg, um zu lernen, ist, immer wieder zu versuchen, mathematische Brüche zu vereinfachen. Die Antworten stehen unter den Problemen.
4(x+2)(x-13)
(4x+8)Antworten: (x=13)
2x-x
5xAntworten:(2x-1)/5

Methode 3 von 3: Tricks zur Lösung kniffligerer Probleme

Bildtitel Simplify Algebraic Fractions Step 10

1. Brüche `invertieren`, um durch negative Zahlen zu faktorisieren. Nehmen wir an, wir haben die folgende Gleichung:
3(x-4)
5(4-x)
Beachten Sie, wie (x-4) und (4-x) fast sind identisch, können aber nicht durchgestrichen werden, da sie vertauscht sind. (x - 4) kann jedoch als -1 * (4 - x) geschrieben werden, genauso wie Sie (4 + 2x) als 2 * (2 + x) umschreiben. Dies wird als `Aus der Klammer herausbringen` bezeichnet.
-1 *3(4-x)
5(4-x)
Jetzt können wir die beiden identischen (4-x) einfach weglassen:
-1 * 3~~(4-x)~~
5~~(4-x)~~
Daraus folgt die abschließende Antwort: -3/5

Bildtitel Simplify Algebraic Fractions Step 11

2. Erkenne den Unterschied von zwei Quadraten während der Arbeit. Die Differenz zweier Quadrate ist einfach das Subtrahieren einer quadrierten Zahl von einer anderen, wie der Ausdruck (a - b). Die Differenz perfekter Quadrate wird immer in zwei Teilen vereinfacht, indem man die Quadratwurzeln addiert und subtrahiert. In jedem Fall können Sie die Differenz perfekter Quadrate wie folgt vereinfachen:
a - b = (a+b)(a-b) Dies kann sehr hilfreich sein, wenn Sie versuchen, ähnliche Terme in mathematischen Brüchen zu finden.

Beispiel: x - 25 = (x+5)(x-5)

Bildtitel Simplify Algebraic Fractions Step 12

3. vereinfachen Polynome. Polynome oder Polynome sind komplexe algebraische Ausdrücke mit mehr als zwei Termen, wie zum Beispiel: x + 4x + 3. Glücklicherweise können viele Polynome durch "Faktorisierung" vereinfacht werden. Der vorherige Ausdruck kann beispielsweise umgeschrieben werden als (x+3)(x+1).

Bildtitel Simplify Algebraic Fractions Step 13

4. Denken Sie daran, dass Variablen auch faktorisiert werden können. Dies ist besonders nützlich für Ausdrücke mit Exponenten wie x + x. Sie können den größten Exponenten als Faktor weglassen. In diesem Fall: x + x = x(x + 1).

Tipps

Überprüfen Sie Ihre Arbeit beim Faktorisieren, indem Sie den Faktor wieder in die Gleichung multiplizieren – Sie erhalten die gleiche Zahl, mit der Sie begonnen haben.
Eliminieren Sie immer die größtmöglichen Zahlen, um Ihre Gleichung vollständig zu vereinfachen.