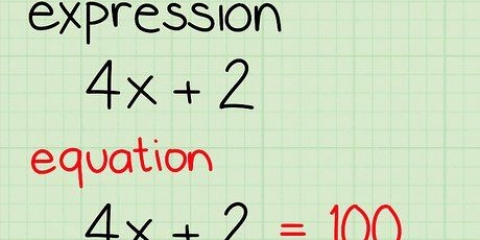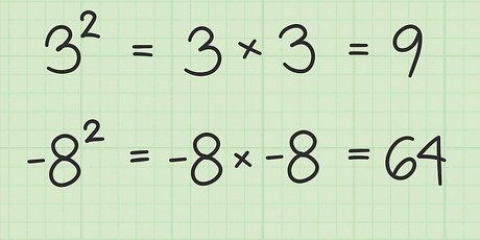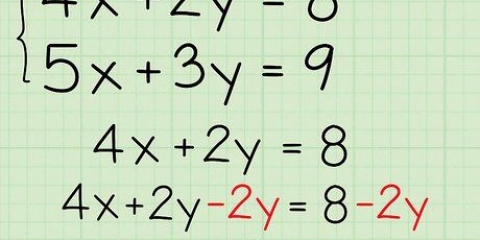Zum Beispiel, 

Zum Beispiel zu  in
in  um zu isolieren, ziehst du
um zu isolieren, ziehst du  von beiden Seiten der Gleichung die Gleichung:
von beiden Seiten der Gleichung die Gleichung:




Zum Beispiel zu  gelöst werden in
gelöst werden in  , dividiere jede Seite der Gleichung durch
, dividiere jede Seite der Gleichung durch  :
:



Die Lösung von ist also ist
ist  .
. 

Zum Beispiel umschreiben  also wenn
also wenn  .
. 
Zum Beispiel,  .
. 
Zum Beispiel für das quadratische Polynom  , Du musst zwei Zahlen finden (
, Du musst zwei Zahlen finden ( und
und  ), wahr
), wahr  und
und  .
. Wegen dir  Sie wissen, dass eine der Zahlen negativ sein wird.
Sie wissen, dass eine der Zahlen negativ sein wird. Das solltest du sehen  und
und  . Also spaltest du dich auf
. Also spaltest du dich auf  auf in
auf in  und schreibe das quadratische Polynom um:
und schreibe das quadratische Polynom um:  .
. 
Zum Beispiel die ersten beiden Terme im Polynom  sind
sind  . Ein in beiden vorkommender Begriff ist
. Ein in beiden vorkommender Begriff ist  . Dies wird die aufgelöste Gruppe
. Dies wird die aufgelöste Gruppe  .
. 
Zum Beispiel die zweiten beiden Terme im Polynom  sind
sind  . Ein in beiden vorkommender Begriff ist
. Ein in beiden vorkommender Begriff ist  . Ebenso die aufgelöste Gruppe
. Ebenso die aufgelöste Gruppe  .
. 
Zum Beispiel wird nach der Faktorisierung durch Gruppierung . zu  gleicht
gleicht  .
. Das erste Binomial ist  .
. Das zweite Binomial ist  .
. Also das ursprüngliche quadratische Polynom,  kann als faktorisierter Ausdruck geschrieben werden
kann als faktorisierter Ausdruck geschrieben werden  .
. 
Um zum Beispiel die erste Lösung von zu finden  , setze den ersten binomialen Ausdruck gleich
, setze den ersten binomialen Ausdruck gleich  und verliere dich
und verliere dich  an. Daher:
an. Daher:



Also, die erste Lösung des quadratischen Polynoms ist
ist  .
. 
Um zum Beispiel die zweite Lösung für zu finden  , setze den zweiten binomialen Ausdruck gleich
, setze den zweiten binomialen Ausdruck gleich  und verliere dich
und verliere dich  an. Daher:
an. Daher:



Die zweite Lösung des quadratischen Polynoms ist also gleicht
gleicht  .
.
Polynome lösen
Ein Polynom ist ein Ausdruck aus Addition und Subtraktion von Termen. Ein Term kann aus Variablen, Konstanten und Koeffizienten bestehen. Beim Lösen von Polynomen versucht man normalerweise herauszufinden, für welche Punkte x = 0. Polynome niedrigsten Grades haben eine oder zwei Lösungen, je nachdem, ob es sich um lineare Polynome oder quadratische Polynome handelt. Diese Arten von Polynomen können leicht mit elementarer Algebra und Faktorisierung gelöst werden. Um Polynome höheren Grades zu lösen, kannst du Artikel auf wikiHow lesen.
Schritte
Methode 1 von 2: Lösen eines linearen Polynoms

1. Bestimmen Sie, ob Sie es mit einem linearen Polynom zu tun haben. Ein lineares Polynom ist ein Polynom ersten Grades. Dies bedeutet, dass keine Variable einen Exponenten (oder einen Exponenten größer als 1) hat. Da dies ein Polynom ersten Grades ist, hat es genau eine Lösung.
- Zum Beispiel,
ist ein lineares Polynom (oder Polynom), weil die Variable
hat keinen Exponenten (was einem Exponenten von 1 entspricht).

2. Machen Sie die Gleichung gleich Null. Dies ist ein notwendiger Schritt zum Lösen aller Polynome.


3. Verschieben Sie den Variablenterm zur Seite. Tun Sie dies, indem Sie die Konstante von beiden Seiten der Gleichung addieren oder subtrahieren. Eine Konstante ist ein Term ohne Variable.
 in
in  um zu isolieren, ziehst du
um zu isolieren, ziehst du  von beiden Seiten der Gleichung die Gleichung:
von beiden Seiten der Gleichung die Gleichung:



4. Löse die Variable. Normalerweise müssen Sie jede Seite der Gleichung durch die Konstante dividieren. Damit erhältst du die Lösung des Polynoms.
 gelöst werden in
gelöst werden in  , dividiere jede Seite der Gleichung durch
, dividiere jede Seite der Gleichung durch  :
:


Die Lösung von ist also
 ist
ist  .
.Methode 2 von 2: Lösen eines quadratischen Polynoms

1. Bestimmen Sie, ob Sie es mit einem quadratischen Polynom zu tun haben. Ein quadratisches Polynom ist eine quadratische Gleichung. Dies bedeutet, dass keine Variable einen Exponenten größer als 2 . hat. Da es sich um ein Polynom zweiten Grades handelt, gibt es zwei Lösungen.
- Zum Beispiel,
ist ein quadratisches Polynom, denn die Variable
ein
hat als Exponent.

2. Stellen Sie sicher, dass das Polynom in der Reihenfolge des Grades geschrieben ist. Dies bedeutet, dass der Term mit Exponent  wird zuerst aufgeführt, gefolgt vom Term ersten Grades, dann die Konstante.
wird zuerst aufgeführt, gefolgt vom Term ersten Grades, dann die Konstante.
 wird zuerst aufgeführt, gefolgt vom Term ersten Grades, dann die Konstante.
wird zuerst aufgeführt, gefolgt vom Term ersten Grades, dann die Konstante. also wenn
also wenn  .
.
3. Machen Sie die Gleichung gleich Null. Dies ist ein notwendiger Schritt zum Lösen aller Polynome.
 .
.
4. Schreiben Sie den Ausdruck in einen Vierterm-Ausdruck um. Sie tun dies, indem Sie das Erstsemester (de  Begriff). Sie suchen zwei Zahlen, deren Summe gleich dem Koeffizienten ersten Grades ist und deren Produkt gleich der Konstanten . ist.
Begriff). Sie suchen zwei Zahlen, deren Summe gleich dem Koeffizienten ersten Grades ist und deren Produkt gleich der Konstanten . ist.
 Begriff). Sie suchen zwei Zahlen, deren Summe gleich dem Koeffizienten ersten Grades ist und deren Produkt gleich der Konstanten . ist.
Begriff). Sie suchen zwei Zahlen, deren Summe gleich dem Koeffizienten ersten Grades ist und deren Produkt gleich der Konstanten . ist. , Du musst zwei Zahlen finden (
, Du musst zwei Zahlen finden ( und
und  ), wahr
), wahr  und
und  .
. Sie wissen, dass eine der Zahlen negativ sein wird.
Sie wissen, dass eine der Zahlen negativ sein wird. und
und  . Also spaltest du dich auf
. Also spaltest du dich auf  auf in
auf in  und schreibe das quadratische Polynom um:
und schreibe das quadratische Polynom um:  .
.
5. Faktor nach Gruppierung. Sie tun dies, indem Sie einen Term faktorisieren, der den ersten beiden Bedingungen im Polynom entspricht.
 sind
sind  . Ein in beiden vorkommender Begriff ist
. Ein in beiden vorkommender Begriff ist  . Dies wird die aufgelöste Gruppe
. Dies wird die aufgelöste Gruppe  .
.
6. Faktorisieren Sie die zweite Gruppe. Sie tun dies, indem Sie einen Term faktorisieren, der in den zweiten beiden Termen des Polynoms vorkommt.
 sind
sind  . Ein in beiden vorkommender Begriff ist
. Ein in beiden vorkommender Begriff ist  . Ebenso die aufgelöste Gruppe
. Ebenso die aufgelöste Gruppe  .
.
7. Schreiben Sie das Polynom in zwei Binome um. Ein Binomial ist ein Ausdruck mit zwei Termen. Sie haben bereits ein Binomial, den Ausdruck in Klammern für jede Gruppe. Dieser Ausdruck muss für jede Gruppe gleich sein. Das zweite Binomial wird gebildet, indem die beiden Terme aus jeder Gruppe faktorisiert werden.
 gleicht
gleicht  .
. .
. .
. kann als faktorisierter Ausdruck geschrieben werden
kann als faktorisierter Ausdruck geschrieben werden  .
.
8. Finden Sie zuerst die Lösung. Sie tun dies, indem Sie lösen  im ersten Binomial.
im ersten Binomial.
 im ersten Binomial.
im ersten Binomial. , setze den ersten binomialen Ausdruck gleich
, setze den ersten binomialen Ausdruck gleich  und verliere dich
und verliere dich  an. Daher:
an. Daher:


Also, die erste Lösung des quadratischen Polynoms
 ist
ist  .
.
9. Bestimmen Sie die zweite Lösung. Du machst das durch  im zweiten Binomial lösen.
im zweiten Binomial lösen.
 im zweiten Binomial lösen.
im zweiten Binomial lösen. , setze den zweiten binomialen Ausdruck gleich
, setze den zweiten binomialen Ausdruck gleich  und verliere dich
und verliere dich  an. Daher:
an. Daher:


Die zweite Lösung des quadratischen Polynoms ist also
 gleicht
gleicht  .
.Tipps
- Machen Sie sich keine Sorgen über Variablen wie t oder wenn Sie eine Gleichung haben, die f(x) anstelle von 0 . entspricht. Wenn die Frage Wurzeln, Nullen oder Faktoren sehen möchte, behandeln Sie sie wie jedes andere Problem.
- Denken Sie bei der Arbeit an die Reihenfolge der Operationen - zuerst die Klammern löschen, dann die Multiplikation und Division durchführen und schließlich die Addition und Subtraktion.
Оцените, пожалуйста статью