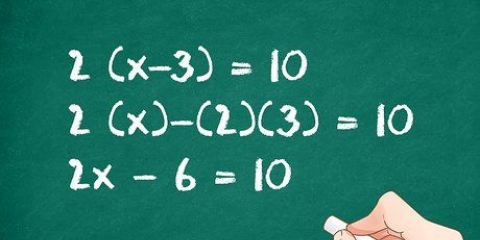3x + 5 + 4x - x + 2x + 9 = 3x - x + 4x + 2x + 5 + 9 = 2x + 6x + 14 
3x + 15 = 9x + 30 Sie sehen, dass jeder Koeffizient durch 3 . teilbar ist. Eliminiere die Zahl 3, indem du jeden Term durch 3 teilst, um die Gleichung zu vereinfachen. 3x/3 + 15/3 = 9x/3 + 30/3 = x + 5 = 3x + 10 
(3 + 5) x 10 + 4 Zuerst die Operationen in Klammern: = (8) x 10 + 4 Dann erhöhen wir die Leistung: = 64 x 10 + 4 Dann die Multiplikation: = 640 + 4 Und zum Schluss addieren wir: = 644 
5x + 15 = 65 = 5x/5 + 15/5 = 65/5 = x + 3 = 13 = x = 10 

2x + 12 = 44 Ziehe zuerst 12 von beiden Seiten ab. 2x + 12 -12 = 44 -12 = 2x = 32 Teilen Sie nun beide Seiten durch 2. 2x/2 = 32/2 = x = 16 Lösen Sie, indem Sie die Quadratwurzel beider Seiten ziehen, denn das macht x gleich x. x = √16 = Geben Sie beide Antworten an: x = 4, -4 
(x + 3)/6 = 2/3 Zuerst multiplizieren Sie kreuzweise, um den Bruch loszuwerden. Multipliziere den Zähler des einen Bruchs mit dem Nenner des anderen Bruchs. (x + 3) x 3 = 2 x 6 = 3x + 9 = 12 Dann kombinierst du gleiche Begriffe. Kombinieren Sie die konstanten Terme 9 und 12, indem Sie 9 von beiden Seiten subtrahieren. 3x + 9 - 9 = 12 - 9 = 3x = 3 Isolieren Sie die Variable x, indem Sie beide Seiten durch 3 teilen und Sie haben die Antwort. 3x/3 = 3/3 = x = 1 
(2x+9) - 5 = 0 Verschiebe zuerst alles, was nicht unter dem Radikal ist, auf die andere Seite der Gleichung: (2x+9) = 5 Dann beide Seiten quadrieren, um das Radikal zu entfernen: (√(2x+9)) = 5 = 2x + 9 = 25 Jetzt können Sie die Gleichung wie gewohnt lösen, indem Sie die Konstanten kombinieren und die Variable isolieren: 2x = 25 - 9 = 2x = 16 x = 8 
Für den Absolutwert errechnen Sie das so, indem Sie den Absolutwert isolieren und dann entfernen: |4x +2| - 6 = 8 = |4x +2| = 8 + 6 = |4x +2| = 14 = 4x + 2 = 14 = 4x = 12 x = 3 Lösen Sie dies nun erneut, indem Sie das Vorzeichen des Termes auf der anderen Seite der Gleichung umkehren, nachdem Sie den Absolutwert isoliert haben: |4x +2| = 14 = 4x + 2 = -14 4x = -14 -2 4x = -16 4x/4 = -16/4 = x = -4 Geben Sie nun beide Antworten an: x = -4, 3
Einen algebraischen ausdruck lösen
Ein algebraischer Ausdruck ist ein mathematischer Ausdruck, der Zahlen und/oder Variablen enthält. Obwohl es nicht gelöst werden kann, weil es kein Gleichheitszeichen (=) enthält, kann es vereinfacht werden. Sie können jedoch mathematische Gleichungen lösen, algebraische Ausdrücke enthalten, die durch ein Gleichheitszeichen getrennt sind. Wenn Sie dieses mathematische Konzept beherrschen möchten, lesen Sie Schritt 1 weiter, um loszulegen.
Schritte
Teil 1 von 2: Die Grundlagen verstehen

1. Verstehe den Unterschied zwischen einem algebraischen Ausdruck und einer algebraischen Gleichung. Ein algebraischer Ausdruck ist ein mathematischer Ausdruck, der Zahlen und/oder Variablen enthält. Es enthält kein Gleichheitszeichen und kann nicht aufgelöst werden. Eine algebraische Gleichung kann jedoch gelöst werden und beinhaltet eine Reihe von algebraischen Ausdrücken, die durch ein Gleichheitszeichen getrennt sind. Hier sind einige Beispiele:
- Algebraischer Ausdruck: 4x + 2
- Algebraische Gleichung: 4x + 2 = 100

2. Erfahren Sie, wie Sie ähnliche Begriffe kombinieren. Das Kombinieren gleicher Terme bedeutet einfach das Addieren (oder Subtrahieren) der Terme gleichen Grades. Das bedeutet, dass alle x-Terme mit anderen x-Termen kombiniert werden können, alle x-Terme mit x-Termen kombiniert werden können und alle Konstanten (Zahlen, die nicht mit Variablen verknüpft sind, wie 8 oder 5) können auch addiert oder kombiniert werden mit gegenseitig. Hier ist ein Beispiel:

3. Lerne, wie man eine Zahl faktorisiert. Wenn Sie es mit einer algebraischen Gleichung zu tun haben, d. h. auf beiden Seiten eines Gleichheitszeichens steht ein Ausdruck, können Sie dies vereinfachen, indem Sie den gemeinsamen Begriff eliminieren. Schauen Sie sich die Koeffizienten aller Bedingungen an (die Zahlen vor den Variablen oder die Konstanten) und sehen Sie, ob es eine Zahl gibt, die Sie "wegarbeiten" können, indem Sie jeden Term durch diese Zahl teilen. Wenn Sie dies können, haben Sie die Gleichung vereinfacht und sind auf dem Weg, sie zu lösen. So funktioniert das:

4. Kennen Sie die Reihenfolge der Operationen. Die Reihenfolge der Operationen, auch bekannt als die mnemonische `Wie man die Unzulänglichkeiten beseitigt`, gibt die Reihenfolge an, in der Sie die verschiedenen mathematischen Operationen ausführen sollten. Die Reihenfolge ist: Klammern, Exponentiation, Rooting, Multiplikation, Division, Addition und Subtraktion. Hier ist ein Beispiel dafür, wie die Reihenfolge der Operationen funktioniert:

5. Lernen Sie, eine Variable zu isolieren. Wenn Sie eine algebraische Gleichung lösen möchten, besteht Ihr Ziel darin, die Variable, die oft als x bezeichnet wird, auf der einen Seite der Gleichung und die konstanten Terme auf der anderen Seite der Gleichung zu erhalten. Sie können x isolieren, indem Sie dividieren, multiplizieren, addieren, subtrahieren, die Quadratwurzel bestimmen oder andere Operationen. Sobald Sie x isoliert haben, können Sie mit der Lösung beginnen. So geht`s:
Teil 2 von 2: Eine algebraische Gleichung lösen

1. Löse eine einfache lineare algebraische Gleichung. Eine lineare algebraische Gleichung ist schön und einfach und verwendet nur die Konstanten und Variablen ersten Grades (keine Potenzen oder andere Komplexität). Um dies zu lösen, müssen Sie bei Bedarf nur multiplizieren, dividieren, addieren oder subtrahieren, um die Variable zu isolieren und nach `x` aufzulösen. So geht`s:
- 4x + 16 = 25 -3x =
- 4x = 25 -16 - 3x
- 4x + 3x = 25 -16 =
- 7x = 9
- 7x/7 = 9/7 =
- x = 9/7

2. Löse eine algebraische Gleichung mit Potenzen (Exponenten). Wenn die Gleichung Potenzen hat, müssen Sie nur einen Weg finden, die Potenz auf einer Seite der Gleichung zu isolieren und dann danach aufzulösen, indem Sie die Potenz "entfernen", indem Sie die Quadratwurzel sowohl der Potenz als auch der der . ermitteln konstant auf der anderen Seite der Gleichung. So geht`s:

3. Löse einen algebraischen Ausdruck mit Brüchen. Um einen algebraischen Ausdruck zu lösen, der Brüche enthält, müssen Sie die Brüche kreuzmultiplizieren, ähnliche Terme kombinieren und dann die Variable isolieren. So geht`s:

4. Löse einen algebraischen Ausdruck. Wenn Sie es mit einem algebraischen Ausdruck mit Radikalen zu tun haben, müssen Sie nur eine Möglichkeit finden, beide Seiten zu quadrieren, damit Sie den Radikal eliminieren und nach der Variablen auflösen können. So geht`s:

5. Löse einen algebraischen Ausdruck, der einen Absolutwert enthält. Der Absolutwert einer Zahl stellt ihren Wert dar, unabhängig davon, ob er positiv oder negativ ist; der Absolutwert ist immer positiv. Der Absolutwert von -3 (auch bekannt als |3|) beträgt also beispielsweise nur 3. Um den Absolutwert zu finden, isolieren Sie den Absolutwert und lösen Sie dann zweimal nach x auf (sowohl für x, wo der Absolutwert einfach entfernt wird, als auch für x, wo die Terme auf der anderen Seite des Gleichheitszeichens das Vorzeichen von positiv zu negativ geändert haben und umgekehrt). Das geht so:
Tipps
- Um Ihre Antwort zu überprüfen, können Sie zu wolfram-alpha gehen.com geh. Dort erhalten Sie die Antwort, oft in den beiden Schritten angezeigt.
- Wenn du fertig bist, ersetze die Variable durch die Antwort und löse dann die Summe, um zu sehen, ob sie richtig ist. Wenn ja, herzlichen Glückwunsch, fertig! Du hast gerade eine algebraische Gleichung gelöst!
- Der Grad eines Polynoms ist die höchste Potenz innerhalb der Terme.
"Einen algebraischen ausdruck lösen"
Оцените, пожалуйста статью