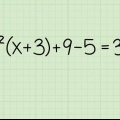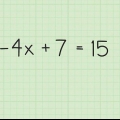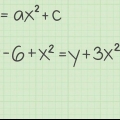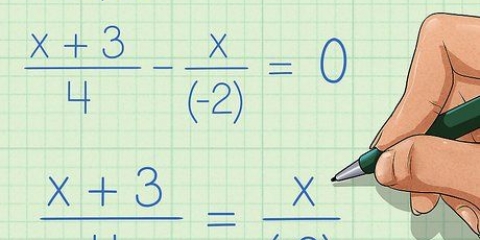Die Verteilungseigenschaft verwenden, um eine Gleichung zu lösen

Schritte
Tipps

Die Verteilungseigenschaft ist eine mathematische Regel zur Vereinfachung einer Gleichung mit Klammern. Sie haben wahrscheinlich schon früh gelernt, dass Sie zuerst die Operationen in Klammern ausführen müssen, aber mit algebraischen Ausdrücken ist das nicht immer möglich. Die Verteilungseigenschaft ermöglicht es Ihnen, den Term außerhalb der Klammern mit den Termen darin zu multiplizieren. Man muss aufpassen, dass man es richtig macht, sonst können Informationen verloren gehen und der Vergleich stimmt nicht mehr. Sie können auch die Verteilungseigenschaft verwenden, um Gleichungen mit Brüchen zu vereinfachen.

Schritte

Methode 1 von 4: Verwenden der fundamentalen Verteilungseigenschaft

Bildtitel Verwenden Sie die Verteilungseigenschaft, um eine Gleichung zu lösen Schritt 1

1. Multiplizieren Sie den Ausdruck außerhalb der Klammern mit einem beliebigen Ausdruck innerhalb der Klammern. Dazu teilt man den äußeren Term im Wesentlichen auf die inneren Terme auf. Multiplizieren Sie den Ausdruck außerhalb der Klammern mit dem ersten Ausdruck innerhalb der Klammern. Dann multiplizierst du es mit dem zweiten Term. Wenn mehr als zwei Begriffe vorhanden sind, verteilen Sie den Begriff außerhalb der Klammern weiterhin auf alle Begriffe innerhalb der Klammern. Lassen Sie die Operatoren (Plus oder Minus) einfach in Klammern.

$2 (x - 3) = 10$ $2(x-3)=10$
$2 (x) - (2) (3) = 10$ $2(x)-(2)(3)=10$
$2 x - 6 = 10$ $2x-6=10$

Bildtitel Verwenden Sie die Verteilungseigenschaft, um eine Gleichung zu lösen Schritt 2

2. Kombiniere ähnliche Begriffe. Bevor Sie die Gleichung lösen können, müssen Sie gleiche Terme kombinieren. Kombinieren Sie alle numerischen Begriffe miteinander. Außerdem kombinierst du alle variablen Begriffe separat. Um die Gleichung zu vereinfachen, ordnen Sie die Terme so an, dass die Variablen auf der einen Seite des Gleichheitszeichens und die Konstanten (nur die Zahlen) auf der anderen Seite stehen.

2 x - 6 = 10

$2x-6=10$ ....(ursprüngliches Problem)

2 x - 6 (+ 6) = 10 (+ 6)

$2x-6(+6)=10(+6)$ .... (auf beiden Seiten 6 hinzufügen)

2 x = 16

$2x=16$ .... (Variable links; konstant rechts)

Bildtitel Verwenden Sie die Verteilungseigenschaft, um eine Gleichung zu lösen Schritt 3

3. Löse die Gleichung. lose

x

$x$ indem man beide Seiten der Gleichung durch den Koeffizienten für die Variable teilt.

2 x = 16

$2x=16$ ....(ursprüngliches Problem)

2 x / 2 = 16 / 2

$2x/2=16/2$ ....(beide Seiten durch 2 teilen)

x = 8

$x=8$ ....(Lösung)

Methode 2 von 4: Negative Koeffizienten verteilen

Bildtitel Verwenden Sie die Verteilungseigenschaft, um eine Gleichung zu lösen Schritt 4

1. Verteile eine negative Zahl zusammen mit dem Minuszeichen. Wenn Sie einen Begriff oder mehrere Begriffe in Klammern mit einer negativen Zahl multiplizieren, achten Sie darauf, dass Sie jedem Begriff in den Klammern das Minuszeichen zuweisen.

Denken Sie an die Grundregeln für die Multiplikation mit negativen Zahlen:

Minus x Minus = Plus.
Minus x Plus = Minus.

Schauen Sie sich das folgende Beispiel an:

- 4 (9 - 3 x) = 48

$-4(9-3x)=48$ .... (ursprüngliches Problem)

- 4 (9) - (- 4) (3 x) = 48

$-4(9)-(-4)(3x)=48$ ....(multiplizieren Sie -4 mit jedem Begriff)

- 36 - (- 12 x) = 48

$-36-(-12x)=48$ ....(vereinfache die Multiplikation)

- 36 + 12 x = 48

$-36+12x=48$ ....(beachten Sie, dass `minus -12` dasselbe wie +12 ist)

Bildtitel Verwenden Sie die Verteilungseigenschaft, um eine Gleichung zu lösen Schritt 5

2. Kombiniere ähnliche Begriffe. Nachdem Sie die Verteilung abgeschlossen haben, müssen Sie die Gleichung vereinfachen, indem Sie alle variablen Terme auf die eine Seite des Gleichheitszeichens und alle Zahlen ohne Variablen auf die andere Seite verschieben. Sie tun dies durch eine Kombination aus Addition oder Subtraktion.

- 36 + 12 x = 48

$-36+12x=48$ ....(ursprüngliches Problem)

- 36 (+ 36) + 12 x = 48 + 36

$-36(+36)+12x=48+36$ ....(füge 36 zu jeder Seite hinzu)

12 x = 84

$12x=84$ ....(vereinfachen Sie die Addition, um die Variable zu isolieren)

Bildtitel Verwenden Sie die Verteilungseigenschaft, um eine Gleichung zu lösen Schritt 6

3. Teilen, um die endgültige Lösung zu erhalten. Lösen Sie die Gleichung, indem Sie beide Seiten der Gleichung durch den Koeffizienten der Variablen dividieren. Dies sollte eine einzige Variable auf der einen Seite der Gleichung ergeben, mit dem Ergebnis auf der anderen Seite.

12 x = 84

$12x=84$ ....(ursprüngliches Problem)

12 x / 12 = 84 / 12

$12x/12=84/12$ ....(beide Seiten durch 12 teilen)

x = 7

$x=7$ ....(Lösung)

Bildtitel Verwenden Sie die Verteilungseigenschaft, um eine Gleichung zu lösen Schritt 7

4. Subtraktion als Addition behandeln (von -1). Wenn Sie in einem Algebra-Problem ein Minuszeichen sehen, insbesondere wenn es vor einer Klammer steht, heißt es im Wesentlichen + (-1). Dies hilft, das Minuszeichen richtig auf alle Begriffe in Klammern zu verteilen. Dann löse das Problem wie zuvor.

Betrachten Sie zum Beispiel das Problem,

4 x - (x + 2) = 4

$4x-(x+2)=4$ . Um sicherzustellen, dass Sie das Minuszeichen richtig verteilt haben, schreiben Sie das Problem wie folgt um:

4 x + (- 1) (x + 2) = 4

$4x+(-1)(x+2)=4$

Dann verteilen Sie -1 über die Terme in Klammern wie folgt:

4 x + (- 1) (x + 2) = 4

$4x+(-1)(x+2)=4$ ....(geändertes Problem)

4 x - x - 2 = 4

$4x-x-2=4$ ....(multiplizieren Sie -1 mit x und mit 2)

3 x - 2 = 4

$3x-2=4$ ....(Begriffe kombinieren)

3 x - 2 + 2 = 4 + 2

$3x-2+2=4+2$ ....(auf beiden Seiten 2 hinzufügen)

3 x = 6

$3x=6$ ....(Begriffe vereinfachen)

3 x / 3 = 6 / 3

$3x/3=6/3$ ....(beide Seiten durch 3 teilen)

x = 2

$x=2$ ....(Lösung)

Methode 3 von 4: Verwenden Sie die Verteilungseigenschaft, um Brüche zu vereinfachen

Bildtitel Verwenden Sie die Verteilungseigenschaft, um eine Gleichung zu lösen Schritt 8

1. Finden Sie heraus, ob es Bruchkoeffizienten oder Konstanten gibt. Manchmal müssen Sie möglicherweise ein Problem mit Brüchen als Koeffizienten oder Konstanten lösen. Sie können sie so belassen wie sie sind und die Grundregeln der Algebra auf sie anwenden, um das Problem zu lösen. Durch die Verwendung der Distributiveigenschaft können Sie die Lösung jedoch oft vereinfachen, indem Sie die Brüche in ganze Zahlen umwandeln.

Sehen Sie sich das folgende Beispiel an $x - 3 = \frac{x}{3} + \frac{1}{6}$ $x-3={frac{x}{3}}+{frac{1}{6}}$ . Die Brüche in diesem Beispiel sind $\frac{x}{3}$ ${frac{x}{3}}$ und $\frac{1}{6}$ ${frac{1}{6}}$ .

Bildtitel Verwenden Sie die Verteilungseigenschaft, um eine Gleichung zu lösen Schritt 9

2. Finden Sie das kleinste gemeinsame Vielfache (LCM) für alle Nenner. In diesem Schritt können Sie alle ganzen Zahlen ignorieren. Schau dir einfach die Brüche an und bestimme den LCF für alle Nenner. Bestimmen Sie die kgf indem man nach der kleinsten Zahl sucht, die ein Vielfaches der Nenner beider Brüche in der Gleichung ist. In diesem Beispiel sind die Nenner 3 und 6, also ist 6 das kgf.

Bildtitel Verwenden Sie die Verteilungseigenschaft, um eine Gleichung zu lösen Schritt 10

3. Multiplizieren Sie alle Terme der Gleichung mit kgf. Denken Sie daran, dass Sie jede beliebige Operation auf eine mathematische Gleichung anwenden können, solange Sie sie auf beiden Seiten ausführen. Multipliziert man jeden Term der Gleichung mit dem lcg, heben sich die Terme gegenseitig auf und werden zu ganzen Zahlen. Setzen Sie Ihre Klammern um die gesamte linke und rechte Seite der Gleichung und verteilen Sie dann:

x - 3 = \frac{x}{3} + \frac{1}{6}

$x-3={frac{x}{3}}+{frac{1}{6}}$ ....(Originalgleichung)

(x - 3) = (\frac{x}{3} + \frac{1}{6})

$(x-3)=({frac{x}{3}}+{frac{1}{6}})$ ....(Klammern anwenden)

6 (x - 3) = 6 (\frac{x}{3} + \frac{1}{6})

$6(x-3)=6({frac{x}{3}}+{frac{1}{6}})$ ....(beide Seiten mit kgf multiplizieren)

6 x - 6 (3) = 6 (\frac{x}{3}) + 6 (\frac{1}{6})

$6x-6(3)=6({frac{x}{3}})+6({frac{1}{6}})$ ....(Multiplikation verteilen)

6 x - 18 = 2 x + 1

$6x-18=2x+1$ ....(vereinfachen Sie die Multiplikation)

Bildtitel Verwenden Sie die Verteilungseigenschaft, um eine Gleichung zu lösen Schritt 11

4. Kombiniere ähnliche Begriffe. Kombiniere alle Terme so, dass alle Variablen auf der einen Seite der Gleichung und alle Konstanten auf der anderen Seite sind. Verwenden Sie die grundlegenden Additions- und Subtraktionsoperationen, um Terme von einer Seite der Gleichung auf die andere zu verschieben.

6 x - 18 = 2 x + 1

$6x-18=2x+1$ ....(vereinfachtes Problem)

6 x - 2 x - 18 = 2 x - 2 x + 1

$6x-2x-18=2x-2x+1$ ....(von beiden Seiten 2x abziehen)

4 x - 18 = 1

$4x-18=1$ ....(Vereinfachen Sie die Minussumme)

4 x - 18 + 18 = 1 + 18

$4x-18+18=1+18$ ....(auf beiden Seiten 18 hinzufügen)

4 x = 19

$4x=19$ ....(Ergänzung vereinfachen)

Bildtitel Verwenden Sie die Verteilungseigenschaft, um eine Gleichung zu lösen Schritt 12

5. Löse die Gleichung. Finden Sie die endgültige Lösung, indem Sie beide Seiten der Gleichung durch den Koeffizienten der Variablen dividieren. Damit bleibt x auf der einen Seite der Gleichung und die numerische Lösung auf der anderen.

4 x = 19

$4x=19$ ....(benutzerdefinierte Ausgabe)

4 x / 4 = 19 / 4

$4x/4=19/4$ ....(beide Seiten durch 4 teilen)

x = \frac{19}{4} oder 4 \frac{3}{4}

$x={frac{19}{4}}{text{ oder }}4{frac{3}{4}}$ ....(endgültige Lösung)

Methode 4 von 4: Verteile einen Bruch mit einer Gleichung

Bildtitel Verwenden Sie die Verteilungseigenschaft, um eine Gleichung zu lösen Schritt 13

1. Interpretiere einen Bruch mit einer Gleichung als verteilte Division. Manchmal sehen Sie ein Problem mit mehreren Termen im Zähler eines Bruchs, die über einem gemeinsamen Nenner liegen. Sie müssen dies als Verteilungsproblem behandeln und den Nenner auf jeden Term des Zählers anwenden. Sie können den Bruch umschreiben, um die Verteilung zu zeigen. Folgendermaßen:

$4 x + 8 2 = 4$ ${frac{4x+8}{2}}=4$ .....(ursprüngliches Problem)
$4 x 2 + \frac{8}{2} = 4$ ${frac{4x}{2}}+{frac{8}{2}}=4$ .....(Multiplizieren Sie den Nenner mit jedem Term des Zählers)

Bildtitel Verwenden Sie die Verteilungseigenschaft, um eine Gleichung zu lösen Schritt 14

2. Vereinfache jeden Zähler als separaten Bruch. Nachdem Sie den Divisor auf jeden Term verteilt haben, können Sie jeden Term einzeln vereinfachen.

4 x 2 + \frac{8}{2} = 4

${frac{4x}{2}}+{frac{8}{2}}=4$ .....(benutzerdefinierte Ausgabe)

2 x + 4 = 4

$2x+4=4$ .....(vereinfache die Brüche)

Bildtitel Verwenden Sie die Verteilungseigenschaft, um eine Gleichung zu lösen Schritt 15

3. Isolieren Sie die Variable. Fahren Sie mit der Lösung des Problems fort, indem Sie die Variable auf einer Seite der Gleichung isolieren und die konstanten Terme auf die andere Seite verschieben. Tun Sie dies durch eine Kombination aus Addition und Subtraktion, falls erforderlich.

2 x + 4 = 4

$2x+4=4$ .....(benutzerdefinierte Ausgabe)

2 x + 4 - 4 = 4 - 4

$2x+4-4=4-4$ .....(subtrahiere 4 von beiden Seiten)

2 x = 0

$2x=0$ .....(x auf einer Seite isolieren)

Bildtitel Verwenden Sie die Verteilungseigenschaft, um eine Gleichung zu lösen Schritt 16

4. Dividiere durch den Koeffizienten, um das Problem zu lösen. Im letzten Schritt dividierst du durch den Koeffizienten der Variablen. Dies ergibt die endgültige Lösung mit der einzelnen Variablen auf der einen Seite der Gleichung und der numerischen Lösung auf der anderen.

2 x = 0

$2x=0$ .....(benutzerdefinierte Ausgabe)

2 x / 2 = 0 / 2

$2x/2=0/2$ .....(beide Seiten durch 2 teilen)

x = 0

$x=0$ .....(Lösung)

Bildtitel Verwenden Sie die Verteilungseigenschaft, um eine Gleichung zu lösen Schritt 17

5. Vermeiden Sie den häufigen Fehler, nur einen Begriff zu teilen. Es ist verlockend (aber falsch), den ersten Term des Zählers durch den Nenner zu teilen und den Bruch zu eliminieren. Ein Fehler wie dieser würde für das obige Problem so aussehen:

4 x + 8 2 = 4

${frac{4x+8}{2}}=4$ .....(ursprüngliches Problem)

2 x + 8 = 4

$2x+8=4$ .....(nur 4x wird durch 2 geteilt, statt des vollen Zählers)

2 x + 8 - 8 = 4 - 8

$2x+8-8=4-8$

2 x = - 4

$2x=-4$

x = - 2

$x=-2$ ..... (falsche Lösung)

Bildtitel Verwenden Sie die Verteilungseigenschaft, um eine Gleichung zu lösen Schritt 18

6. Überprüfen Sie die Richtigkeit Ihrer Lösung. Sie können Ihre Arbeit jederzeit überprüfen, indem Sie Ihre Lösung in das ursprüngliche Problem einfügen. Wer vereinfachen will, muss zu einer wahren Aussage kommen. Wenn Sie vereinfachen und eine falsche Aussage als Antwort erhalten, dann ist Ihre Lösung falsch. In diesem Beispiel testen Sie die beiden Lösungen für x = 0 und x =-2, um zu sehen, welche richtig ist.

Beginnen Sie mit Lösung x=0:

4 x + 8 2 = 4

${frac{4x+8}{2}}=4$ .....(ursprüngliches Problem)

4 (0) + 8 2 = 4

${frac{4(0)+8}{2}}=4$ .....(ersetze 0 für x)

0 + 8 2 = 4

${frac{0+8}{2}}=4$

\frac{8}{2} = 4

${frac{8}{2}}=4$

4 = 4

$4=4$ .....(Wahr. Das ist die richtige Lösung.)

Versuchen Sie die `falsche Lösung für x=-2:

4 x + 8 2 = 4

${frac{4x+8}{2}}=4$ .....(ursprüngliches Problem)

4 (- 2) + 8 2 = 4

${frac{4(-2)+8}{2}}=4$ .....(Geben Sie -2 für x ein)

- 8 + 8 2 = 4

${frac{-8+8}{2}}=4$

\frac{0}{2} = 4

${frac{0}{2}}=4$

0 = 4

$0=4$ .....(Falsche Aussage. Daher ist x=-2 falsch.)

Tipps

Sie können auch die Verteilungseigenschaft verwenden, um einige Multiplikationen zu vereinfachen. Sie können Zahlen in Zehner mit Rest teilen, um das Kopfrechnen zu erleichtern. Sie können beispielsweise 8 x 16 als 8(10+6) umschreiben. Dies ist dann einfach 80 + 48 = 128. Ein weiteres Beispiel, 7 x 24 = 7(20 + 4) = 7(20) + 7(4) = 140 + 28 = 168. Üben Sie diese auswendig und Kopfrechnen wird viel einfacher.