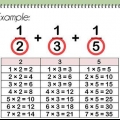
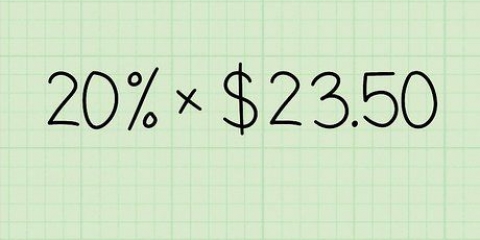2 x 2 x 3 x 5 x 7 = 420.
Der LCF von 20 und 42 beträgt 420.


8 x 1 = 8
8 x 2 = 16
8 x 3 = 24 
Der LCF von 5 und 8 beträgt 40. Dies ist das kleinste gemeinsame Vielfache, da es ein erster auftretender Faktor des gleichen Vielfachen für 5 und 8 ist, und somit die LCF für diese Zahlen.



18/2 = 9, also schreibe 9 unter 18. 12/2 = 6, also schreibe 6 unter 12. 30/2 = 15, also schreibe 15 unter 30. 
Faktor 3 aus diesen Zahlen. 3 ist hier der kleinste Primfaktor, die kleinste durch beide Zahlen teilbare Primzahl.
Teile alle drei Zahlen durch 3 und schreibe das Ergebnis unter diese Zahlen.
9/3 = 3, also schreiben Sie eine 3 unter 9; 6/3 = 2, also schreiben Sie eine 2 unter 6; 15/3 = 5, also schreibst du eine 5 unter 15.

Angenommen, die unteren Zahlen sind 2, 39 und 122, dann dividieren Sie 2 und 122 durch 2, was zu einer neuen unteren Reihe führt: 1, 39 und 61. 
Der LCF von 18, 12 und 30 beträgt 180.

Dann dividiere die zweite Zahl (45) durch den Rest (30). 45/30 = 1 (Rest 15). Also 45 = 1 x 30 + 15.
Dann dividiere den Rest aus dem ersten Schritt (30) durch den Rest aus dem zweiten Schritt (15). 30/15 = 2 (Rest 0). Also 30 = 2 x 15 + 0.
Die GGD von 210 und 45 beträgt 15.
Sie können diese Methode jederzeit verwenden, um die GGD zu finden – hören Sie einfach auf zu teilen, sobald Sie einen Rest von 0 . erreicht haben. 


Finde das kleinste gemeinsame vielfache von zwei zahlen
Das kleinste gemeinsame Vielfache (KGB) einer Zahlengruppe ist die kleinste Zahl, die ein Vielfaches aller Zahlen in der Gruppe ist. Der LCF von 16 und 20 beträgt beispielsweise 80; 80 ist die kleinste Zahl, die sowohl ein Vielfaches von 16 als auch ein Vielfaches von 20 ist. Sie können den LCF von zwei oder mehr Zahlen mit verschiedenen Methoden ermitteln. Wenn Sie wissen möchten, wie Sie den LCF von zwei oder mehr Zahlen finden, folgen Sie diesen Schritten.
Schritte
Methode 1 von 4: Primfaktorzerlegung

1. Bestimme die Primfaktoren beider Zahlen. Dies ist eine ideale Methode für größere Zahlen. Der erste Schritt, um mit dieser Methode das kleinste gemeinsame Vielfache von zwei Zahlen zu finden, besteht darin, beide Zahlen in die multiplizierten Primzahlen einzubeziehen, um diese Zahl als Produkt zu erhalten. Sie können damit beginnen, eine Liste von zwei Zahlen (Faktoren) zu erstellen, die miteinander multipliziert werden, um diese Zahl zu erhalten, und sie dann in ihre Primfaktoren faktorisieren. Angenommen, Sie möchten das kleinste gemeinsame Vielfache von finden 20 und 42. So faktorisieren Sie es. 20 = 2 x 2 x 542 = 2 x 3 x 7

2. Schreibe auf, welche Primzahl in den Primfaktoren jeder Zahl am häufigsten vorkommt. Hier ist eine Liste der Zahlen, die für jede Primzahl im vorherigen Beispiel am häufigsten vorkommen 2 → 2 mal3 → 1 mal5 → 1 mal7 → 1 mal
3. Alle Faktoren zusammen multiplizieren . So finden Sie das EKG des Beispiels:


Methode 2 von 4: Listen Sie alle Vielfachen beider Zahlen auf

1. Listen Sie einige Vielfache der ersten Zahl in aufsteigender Reihenfolge auf. Dies ist eine ideale Methode für kleinere Zahlen, insbesondere für Zahlen kleiner als 10. Für größere Zahlen wird dies nicht empfohlen, da dies schwierig werden kann. Angenommen, Sie möchten das KGV von . ermitteln 5 und8. Sie erstellen zuerst eine Liste der Vielfachen von 55 x 1 = 55 x 2 = 105 x 3 = 15

2. Listen Sie nun einige Vielfache der zweiten Zahl (8) in aufsteigender Reihenfolge auf.
8 x 2 = 16
8 x 3 = 24

3. Probieren Sie für beide Zahlen mehrere Möglichkeiten aus, bis Sie das kleinste gemeinsame Vielfache gefunden haben. In einigen Fällen können Sie die LCF nach einigen Versuchen für jede Zahl finden. Fahren Sie in diesem Beispiel fort, bis Sie ein kleinstes gemeinsames Vielfaches für 5 und 8 . gefunden haben. Das ist dein kgf
5 x 4 = 20
5 x 5 = 25
5 x 6 = 30
5 x 7 = 35
5 x 8 = 40
8 x 4 = 32
8 x 5 = 40
5 x 4 = 20
5 x 5 = 25
5 x 6 = 30
5 x 7 = 35
5 x 8 = 40
8 x 4 = 32
8 x 5 = 40

Methode 3 von 4: Verwenden Sie eine gemeinsame Vielfaches-Tabelle

1. Schreiben Sie die Zahlen oben in eine Tabelle mit gemeinsamen Vielfachen. Lassen Sie links neben den Zahlen etwas Platz und unter den Zahlen so viel Platz wie möglich. Angenommen, wir haben die Zahlen 18, 12 und 30. Schreiben Sie jede Zahl in eine eigene Spalte oben in der Tabelle.

2. Schreibe den kleinsten gemeinsamen Primfaktor der Zahlen in das Feld links. Suchen Sie nach dem kleinsten Primfaktor (wie 2, 3 oder 5), den Sie aus allen Zahlen herausrechnen können. Es sind alle gerade Zahlen, also ist mindestens 2 möglich.

3. Teilen Sie jede der Zahlen, die Sie annehmen, durch den gemeinsamen Primfaktor. Schreiben Sie den Quotienten unter jede Zahl. So wird es aussehen:

4. Wiederholen Sie den Vorgang des Faktorisierens und Dividierens durch den niedrigsten Primfaktor, bis keine Faktoren mehr übrig sind. Wiederholen Sie dies für die Zahlen 9, 6 und 15.




5. Wenn zwei der Zahlen immer noch einen gemeinsamen Primfaktor haben, fahren Sie mit diesem Verfahren fort, bis keine der unteren Zahlen einen gemeinsamen Faktor hat. Mit diesem Beispiel sind Sie jetzt fertig.

6. Multiplizieren Sie alle Zahlen in der ersten Spalte mit den gemeinsamen Primfaktoren, wobei die Zahlen in allen anderen Spalten am Ende stehen. Das ist die KGV. In diesem Beispiel ist das Produkt der Spalte mit den gemeinsamen Faktoren gleich 6 (2 x 3). Multiplizieren Sie 6 mit den Zahlen am Ende der anderen Spalten: 6 x 3 x 2 x 5 = 180.

Methode 4 von 4: Euklids Algorithmus
1. Verwenden Sie den Euklid-Algorithmus, um den größten gemeinsamen Teiler (GGD) von zwei Zahlen zu finden. Angenommen, die beiden Zahlen in einem Beispiel210 und 45 sind. Hier ist ein Beispiel für die Verwendung des Euklid-Algorithmus, um die GGD beider Zahlen zu ermitteln:
- Teilen Sie die erste Zahl durch die zweite: 210/45 = 4 (Rest 30). Dies bedeutet, dass 210 = 4 x 45 + 30.





2. Multiplizieren Sie die beiden ursprünglichen Zahlen. 210 x 45 = 9.450

3. Dividiere das Ergebnis durch die GGD beider Zahlen. 9.450/15 = 630. 630 ist der LCF von 210 und 45.

4. Verwenden Sie den Algorithmus von Euklid, um die LCF von drei Zahlen zu finden. Suchen Sie dazu einfach nach der GCD von zwei Zahlen und verwenden Sie dann diese GGD, um die VCF dieser beiden Zahlen und der dritten Zahl zu finden.
Tipps
- Wenn Sie wissen möchten, ob der VCF kleiner oder größer als das Produkt ist, verwenden Sie diese Methode: Wenn der GGD 1 ist, ist der VCF das Produkt. Wenn der GGD größer als 1 ist, ist der VCGV kleiner als das Produkt.
- Der KGV hat viele Anwendungen. Am häufigsten müssen Brüche beim Addieren oder Subtrahieren denselben Nenner haben; Wenn dies nicht der Fall ist, müssen Sie sie namensgebend machen, damit sie den gleichen Nenner haben. Der beste Weg, dies zu tun, besteht darin, nach dem kleinsten gemeinsamen Nenner zu suchen, der einfach dem LCF der Nenner entspricht. Um zum Beispiel 1/6 + 3/8 zu berechnen, suchen wir den LCF von 6 und 8, also 24, und konvertieren dann jeden Bruch so, dass beide Nenner gleich 24 sind, wobei die Summe wie folgt aussieht: 4/24 + 9/24. Wir können dies jetzt einfach berechnen, indem wir den Zähler zusammenzählen, mit der Antwort: 13/24.
- Wenn Sie den LCF von mehr als 2 Zahlen finden müssen, muss Ihre obige Methode leicht geändert werden, da sie nur für 2 Zahlen gleichzeitig funktioniert. Um beispielsweise den LCF von 16, 20 und 32 zu ermitteln, beginnen wir damit, den LCF von 16 und 20 (was 80 entspricht) und dann den LCF von 80 und 32 zu ermitteln, der 160 . ergibt.
- Um zum Beispiel die CHF 16 und 20 zu finden, nehmen wir die GGD von 16 und 20, was 4 . ergibt. 16 × 20 = 320 und 320 ÷ 4 = 80, also ist 80 das KGV.
- Wenn Sie einen Bruch mit demselben Namen bilden möchten, müssen Sie wissen, wie oft jeder Nenner in die LCF kommt. Mit dieser Methode können Sie den Umrechnungsfaktor ermitteln, indem Sie alle Zahlen am Ende aller anderen Spalten multiplizieren (außer der ersten, in der alle Primfaktoren aufgelistet sind). Um 18 in 180 umzuwandeln, multiplizieren Sie es mit 2 und 5. Um 12 in 180 umzuwandeln, multiplizieren Sie es mit 3 und 5.Um 30 in 180 umzuwandeln, multiplizieren Sie es mit 3 und 2.
Notwendigkeiten
- Bleistift.
- Radiergummi.
- Rechner (optional).
"Finde das kleinste gemeinsame vielfache von zwei zahlen"
Оцените, пожалуйста статью