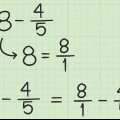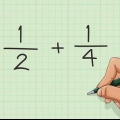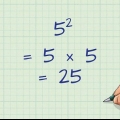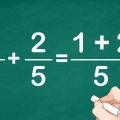18 ÷ 3 = 6, also 2/3 = (2x6)/(3x6)=12/18 18 ÷ 6 = 3, also 5/6 = (5x3)/(6x3)=15/18 18 ÷ 3 = 6, also 1/3 = (1x6)/(3x6)=6/18 

6/18 = (6 6)/(18 ÷ 6) = 1/3 12/18 = (12 6)/(18 6) = 2/3 15/18 = (15 3)/(18 3) = 5/6 Die Antwort ist "1/3, 2/3, 5/6" 

Dies wird als Kreuzmultiplikation bezeichnet, da Sie Zahlen diagonal miteinander multiplizieren. 



Denken Sie daran, das Produkt der Multiplikation immer neben den Bruch zu setzen, dessen Zähler Sie verwendet haben. 
3/5=(3x3)/(5x3)=9/15 2/3=(2x5)/(3x5)=10/15 9/15 ist weniger als 10/15 3/5 ist also weniger als 2/3 

8/3 = 2 + 2/3 9/9 = 1 19/4 = 4 + 3/4 13/6 = 2 + 1/6 
1 ist die kleinste 2 + 2/3 und 2 + 1/6 (wir wissen noch nicht, welches größer ist als das andere) 4 + 3/4 ist die größte 
2/3 = (2x2)/(3x2) = 4/6 1/6 = 1/6 4/6 ist größer als 1/6 2 + 4/6 ist größer als 2 + 1/6 2 + 2/3 ist größer als 2 + 1/6 

Fraktionen nach größe sortieren
Während es einfach ist, Ganzzahlen wie 1, 3 und 8 nach Größe zu ordnen, ist dies bei Brüchen nicht immer offensichtlich. Wenn alle Nenner gleich sind, können Sie sie wie ganze Zahlen anordnen, z. 1/5, 3/5 und 8/5. In anderen Fällen können Sie die Brüche so umwandeln, dass sie den gleichen Nenner haben, ohne den Wert des Bruchs zu ändern. Dies wird mit Übung einfacher und Sie können einige praktische Tricks anwenden, sowohl beim Vergleichen zweier Brüche als auch beim Ordnen von Brüchen, bei denen der Zähler größer als der Nenner ist, die unechten Brüche wie 7/3.
Schritte
Methode 1 von 3: Beliebig viele Brüche bestellen

1. Finden Sie einen gleichen Nenner für alle Brüche. Verwenden Sie eine der folgenden Methoden, um einen Nenner zu finden, oder verringern Sie die Zahl eines Bruchs, mit dem Sie jeden Bruch in der Liste zum einfachen Vergleich neu schreiben können. Das nennst du a gemeinsamer Nenner, oder der kleinster gemeinsamer Nenner wenn dies die kleinstmögliche ist:
- Multipliziere jeden Nenner miteinander. Wenn Sie beispielsweise 2/3, 5/6 und 1/3 vergleichen, multiplizieren Sie diese Nenner miteinander: 3 x 6 = 18. Dies ist eine einfache Methode, die jedoch oft zu einer viel größeren Anzahl führt als die anderen Methoden, die etwas schwieriger sind.
- Oder liste ein Vielfaches jedes Nenners in einer separaten Spalte auf, bis eine Zahl, die häufiger vorkommt, auffällt. Zum Beispiel haben Sie bei 2/3, 5/6 und 1/3 Listenvielfache von 3:3, 6, 9, 12, 15, 18. Dann eine Liste von Vielfachen von 6: 6, 12, 18. Denn 18 in beiden Listen vorkommt, verwenden Sie diese Zahl (Sie können auch 12 verwenden, aber die folgenden Beispiele gehen davon aus, dass Sie 18 verwenden).

2. Wandle jeden Bruch so um, dass er einen gleichen Nenner hat. Denken Sie daran, dass der Wert des Bruchs gleich bleibt, wenn Sie Zähler und Nenner eines Bruchs mit derselben Zahl multiplizieren. Wende diese Technik mit jedem Bruch einzeln an, sodass jeder Bruch den gleichen Nenner hat. Versuchen Sie dies für 2/3, 5/6 und 1/3 mit dem Nenner 18:

3. Ordne die Brüche nach den Zählern. Da nun alle Brüche den gleichen Nenner haben, sind sie leicht zu vergleichen. Bestellen Sie sie vom kleinsten bis zum größten nach der Theke. Dies gibt uns die folgende Liste: 6/18, 12/18, 15/18.

4. Bringe jeden Bruch in seine ursprüngliche Form zurück. Lassen Sie die Brüche in dieser Reihenfolge, aber wandeln Sie sie wieder in den ursprünglichen Bruch um. Sie tun dies, indem Sie sich einfach merken, welcher Bruch zu welchem gehört oder indem Sie die oberen und unteren Zahlen des Bruchs erneut teilen:
Methode 2 von 3: Zwei Brüche mit Kreuzmultiplikation ordnen

1. Schreibe die beiden Brüche nebeneinander. Vergleiche zum Beispiel den Bruch 3/5 und den Bruch 2/3. Schreiben Sie diese nebeneinander: 3/5 links und 2/3 rechts.

2. Multipliziere den Zähler des ersten Bruchs mit dem Nenner des zweiten. Also: 3 x 3 = 9.

3. Schreibe deine Antwort neben den ersten Bruch. Schreibe das Produkt von 3 x 3 = 9 neben den ersten Bruch.

4. Multiplizieren Sie den Zähler der zweite Bruch mit dem Nenner von Erste. Um zu sehen, welche die größte ist, vergleichen wir die Antwort mit einer anderen Multiplikation. Multiplizieren Sie diese beiden Zahlen miteinander. In diesem Beispiel (wir vergleichen 3/5 und 2/3) multiplizieren wir 2 x 5.

5. Schreibe die Antwort neben den zweiten Bruch. Schreibe das Ergebnis von 2 x 5 =10 neben den zweiten Bruch.

6. Vergleichen Sie die Werte der Ergebnisse. Ist ein Wert größer als der andere, ist der Bruch neben dem Ergebnis auch der größte. Da 9 kleiner als 10 ist, ist 3/5 kleiner als 2/3.

7. Wie genau funktioniert das? Was Sie tun, ist, die Brüche so umzuwandeln, dass sie beide den gleichen Nenner haben. Das ist es also, was die Kreuzmultiplikation tatsächlich tut! Es überspringt das eigentliche Aufschreiben der Nenner, da Sie bei gleichen Nennern nur die Zähler vergleichen müssen. Also wie folgt, ohne den kurzen Weg der Kreuzmultiplikation:
Methode 3 von 3: Brüche größer als eins ordnen

1. Verwenden Sie diese Methode für Brüche, bei denen der Zähler größer als der Nenner ist. Ist der Zähler größer als der Nenner, dann ist dieser Bruch größer als 1. 8/3 ist ein Beispiel dafür. Sie können dies auch für Brüche mit demselben Zähler und Nenner verwenden, z. B. 9/9. Dies sind beides Beispiele für "unangemessen" Brüche.
- Sie können für diese Brüche immer noch die anderen Methoden verwenden. Diese Methode hilft Ihnen, diese Brüche besser zu verstehen und ist möglicherweise etwas schneller.

2. Wandle jeden unechten Bruch in einen gemischten Bruch um. Machen Sie es zu einer Kombination aus einer ganzen Zahl und einem Bruch. Manchmal kann man das ganz einfach auswendig machen. Zum Beispiel 9/9 = 1. Verwenden Sie in den schwierigeren Fällen eine lange Division, um herauszufinden, wie oft der Nenner durch den Zähler teilbar ist. Jeder Rest der langen Division bleibt als Bruch. Zum Beispiel:

3. Sortiere die gemischten Zahlen nach der ganzen Zahl. Jetzt, da es keine unechten Brüche mehr gibt, haben Sie eine bessere Vorstellung von der Größe jeder Zahl. Ignoriere zuerst die Brüche und sortiere jede gemischte Zahl nach der ganzen Zahl:

4. Vergleiche bei Bedarf die Brüche in jeder Gruppe. Wenn Sie mehrere gemischte Zahlen mit derselben ganzen Zahl haben, z. B. 2 + 2/3 und 2 + 1/6, vergleichen Sie den Bruch beider Zahlen, um herauszufinden, welcher größer ist. Im Beispiel vergleichen wir 2 + 2/3 und 2 + 1/6 und wandeln die Brüche in denselben Nenner um:

5. Verwenden Sie das Ergebnis, um die Liste der gemischten Zahlen weiter zu sortieren. Die Reihenfolge der gesamten Liste lautet nun: 1, 2 + 1/6, 2 + 2/3, 4 + 3/4.

6. Wandle die gemischten Zahlen wieder in die ursprünglichen Brüche um. Behalten Sie die Reihenfolge bei, aber machen Sie alle Änderungen rückgängig und schreiben Sie die Brüche in die ursprünglichen unechten Brüche um: 9/9, 8/3, 13/6, 19/4.
Tipps
- Bei der Sequenzierung einer großen Anzahl von Fraktionen kann es sinnvoll sein, kleine Gruppen von 2, 3 oder 4 Fraktionen zu vergleichen.
- Es kann zwar hilfreich sein, den kleinsten gemeinsamen Nenner zu finden, aber jeder gemeinsame Nenner funktioniert. Versuchen Sie, 2/3, 5/6 und 1/3 mit einem gemeinsamen Nenner von 36 zu ordnen und sehen Sie, ob Sie das gleiche Ergebnis erhalten.
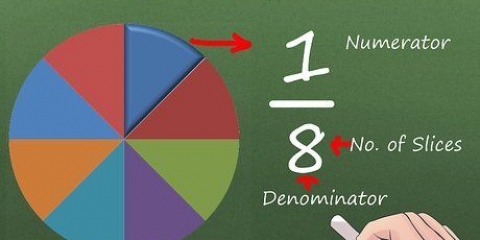
- Wenn die Zähler alle gleich sind, können Sie die Brüche auch schnell bestellen. Zum Beispiel 1/8 < 1/7 < 1/6 < 1/5. Stellen Sie sich das wie eine Pizza vor: Wenn Sie von 1/2 auf 1/8 gehen, schneiden Sie die Pizza in 8 statt in 2 Teile und die Stücke sind kleiner.
"Fraktionen nach größe sortieren"
Оцените, пожалуйста статью