(/2) = /2 × /2 oder (/2). Das Quadrieren jeder Zahl ergibt (/4). 
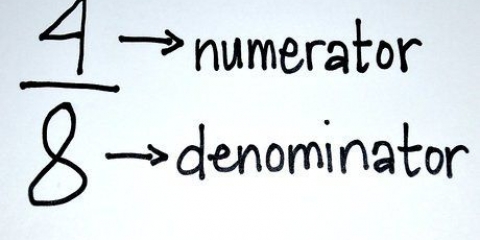
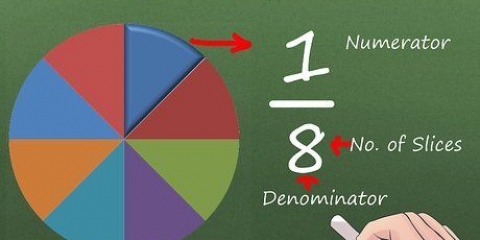
Der Zähler bleibt oben auf dem Bruch und der Nenner bleibt unten. Zum Beispiel: (/2) = (/2 x 2) = (/4). 
Um dies in eine gemischte Zahl umzuwandeln, dividiere 25 durch 4. Dies ist 6 (6 x 4 = 24), mit einem Rest von 1. Daher ist die gemischte Zahl 6/4. 

Zum Beispiel: (-/4) = (–/4) x (-/4) 
Zum Beispiel: (-2) x (-8) = (+16) 
Wenn wir mit dem Beispiel fortfahren, ist der resultierende Bruch eine positive Zahl. (–/4) x (-/4) = (+/16) Es ist üblich, das Pluszeichen bei positiven Zahlen wegzulassen. 
Zum Beispiel: (/16) hat einen gemeinsamen Faktor von vier. Teilen Sie den Bruch durch 4: 4/4 = 1, 16/4 = 4 Schreibe den vereinfachten Bruch um: (/4) 

Zum Beispiel: 16 × (/16) Quadratiere die Klammern und eliminiere den gemeinsamen Faktor von 16: 16 * /16 * /16 Da Sie es hier mit einer 16 als Ganzzahl und zweimal einer 16 im Nenner zu tun haben, können Sie eine davon eliminieren. Schreiben Sie die vereinfachte Gleichung um: 12 × /16 vereinfachen /16 durch Division durch 4: /4 Multiplizieren: 12 × /4 = 36/4 Stimme: 36/4 = 9 
Zum Beispiel: 16 * (/16) Schreibe mit dem quadrierten Zähler und Nenner um: 16 * (/16) Subtrahiere den Exponenten im Nenner: 16 * /16 Stellen Sie sich die ersten 16 als Exponenten von 1:16 . vor. Mit den Regeln zum Subtrahieren von Potenzen/Exponenten subtrahieren Sie die Exponenten voneinander. 16/16, ergibt 16 = 16 oder 1/16. Jetzt fahren Sie fort mit /16 Schreibe den Bruch um und vereinfache ihn: /16 =* /4. Vereinfachen: 12 × /4 = 36/4 Stimme: 36/4 = 9
Quadrieren von brüchen
Das Quadrieren von Brüchen ist eine der einfachsten Operationen, die Sie mit Brüchen ausführen können. Es ist dem Quadrieren von ganzen Zahlen sehr ähnlich, da Sie sowohl den Zähler als auch den Nenner einfach mit sich selbst multiplizieren können. Es gibt einige Fälle, in denen das Vereinfachen des Bruchs vor dem Quadrieren das Verfahren erleichtert. Wenn Sie diese Fertigkeit noch nicht gelernt haben, bietet dieser Artikel einen kurzen Überblick, um Ihr Verständnis zu verbessern.
Schritte
Teil 1 von 3: Brüche quadrieren

1. Verstehe, wie man ganze Zahlen quadriert. Wenn Sie eine Zahl in der zweiten Potenz sehen, wissen Sie, dass Sie die Zahl quadrieren müssen. Dies ist das gleiche wie die Zahl mit sich selbst zu multiplizieren. Zum Beispiel:
- 5 = 5 × 5 = 25

2. Ist dir die Quadratur klar?Brüche funktioniert genauso. Um einen Bruch zu quadrieren, multiplizieren Sie den Bruch mit sich selbst. Eine andere Möglichkeit, darüber nachzudenken, besteht darin, den Zähler mit sich selbst und den Nenner mit sich selbst zu multiplizieren. Zum Beispiel:

3. Multipliziere den Zähler mit sich selbst und den Nenner mit sich selbst. Die tatsächliche Reihenfolge, in der Sie diese Zahlen mit sich selbst multiplizieren, spielt keine Rolle, solange Sie beide Zahlen quadrieren. Beginnen Sie der Einfachheit halber mit dem Zähler: Multiplizieren Sie ihn einfach mit sich selbst. Dann multipliziere den Nenner mit sich selbst.

4.Vereinfachen der Bruchteil, um das zusammenzufassen. Beim Umgang mit Brüchen besteht der letzte Schritt immer darin, den Bruch auf seine einfachste Form zu vereinfachen oder einen unechten Bruch in eine gemischte Zahl umzuwandeln. Unser Beispiel, /4 ist ein unechter Bruch, weil der Zähler größer als der Nenner ist.
Teil 2 von 3: Quadrieren von Brüchen mit negativen Zahlen

1. Suchen Sie nach einem Minuszeichen vor dem Bruch. Wenn es sich um einen negativen Bruch handelt, steht ein Minuszeichen davor. Es ist ratsam, eine negative Zahl immer in Klammern zu setzen, damit Sie wissen, dass sich das Minuszeichen auf die Zahl bezieht und nicht als Minussumme gedacht ist.
- Zum Beispiel: (-/4)

2. Multipliziere den Bruch mit sich selbst. Quadrieren Sie den Bruch wie gewohnt, indem Sie den Zähler mit sich selbst multiplizieren und dann den Nenner mit sich selbst multiplizieren. Du kannst den Bruch auch einfach mit sich selbst multiplizieren.

3. Verstehe, dass die Multiplikation zweier negativer Zahlen eine positive Zahl ergibt. Wenn ein Minuszeichen vorhanden ist, wird der ganze Bruch negativ. Wenn Sie den Bruch quadrieren, multiplizieren Sie zwei negative Zahlen. Wenn zwei negative Zahlen miteinander multipliziert werden, ist das Produkt immer positiv.

4. Entfernen Sie das Minuszeichen nach dem Quadrieren. Wenn Sie den Bruch quadriert haben, haben Sie zwei negative Zahlen multipliziert. Das bedeutet, dass der quadrierte Bruch positiv ist. Vergessen Sie nicht, das Minuszeichen in der endgültigen Antwort wegzulassen.

5. Vereinfachen Sie den Bruch so weit wie möglich. Der letzte Schritt bei der Berechnung von Brüchen besteht darin, zu vereinfachen. Unechte Brüche müssen zuerst zu gemischten Zahlen vereinfacht und dann weiter vereinfacht werden.
Teil 3 von 3: Vereinfachungen und Schnellkorrekturen verwenden

1. Überprüfe, ob du den Bruch machen kannstvereinfachen bevor du es quadrierst. Es ist normalerweise einfacher, Brüche vor dem Quadrieren zu vereinfachen. Denken Sie daran, einen Bruch zu vereinfachen bedeutet, ihn durch einen gemeinsamen Faktor zu teilen, bis 1 die einzige verbleibende Zahl ist, die sowohl durch den Zähler als auch durch den Nenner geteilt werden kann. Einen Bruch zuerst zu vereinfachen bedeutet, dass du ihn am Ende nicht noch einmal vereinfachen musst, wenn die Zahlen größer sind.
- Zum Beispiel: (/16)
- 12 und 16 können beide durch 4 . geteilt werden. 12/4 = 3 und 16/4 = 4; so kannst du/16 vereinfachen zu /4.
- Jetzt können Sie den Bruch /4 quadrieren.
- (/4) = /16, was man nicht mehr vereinfachen kann.
- Um dies zu beweisen, quadrieren wir den ursprünglichen Bruch ohne zu vereinfachen:
- (/16) = (/16x16) = (/256)
- (/256) hat einen gemeinsamen Faktor von 16. Die Division von Zähler und Nenner durch 16 vereinfacht den Bruch zu (/16), den gleichen Bruch, den wir zuerst durch Vereinfachen erhalten haben.

2. Erfahren Sie, wann Sie mit dem Vereinfachen eines Bruchs warten sollten. Haben Sie es mit komplexeren zu tun? Gleichungen, dann kann es möglich sein, einen der Faktoren zu eliminieren. In einem solchen Fall ist es daher bequemer, mit der Vereinfachung des Bruchs zu warten. Wenn man dem obigen Beispiel einen zusätzlichen Faktor hinzufügt, wird dies klarer.

3. Verstehen Sie, wie Sie dies schnell mit demExponent. Eine andere Möglichkeit, das gleiche Problem zu lösen, besteht darin, zuerst den Exponenten zu vereinfachen. Das Ergebnis wird das gleiche sein, nur über einen anderen Weg erhalten.
Notwendigkeiten
- Papier oder ein Computer
- Bleistift/Kugelschreiber (bei Verwendung von Papier)
Оцените, пожалуйста статью