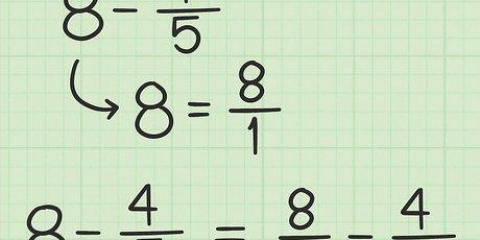In unserem Beispiel würden wir den Rest weglassen und einfach 1 schreib es auf (da unsere Antwort 1 R2 ist). 
In unserem Beispiel ist der Rest gleich 2. Wenn wir dies als Zähler über dem ursprünglichen Nenner (5) einsetzen, erhalten wir 2/5. Wir setzen dies neben unsere Antwort auf die ganze Zahl (1) und erhalten die endgültige gemischte Zahl. Folgendermaßen: 1 2/5. 
Wenn wir aus der Antwort auf unser Beispiel (1 2/5) einen unechten Bruch machen wollen, können wir es so machen: 1 × 5 = 5 → (2 + 5)/5 = 7/5 

99/5 – wie oft geht 5 in 99? Da 5 in 100 genau 20-mal geht, können Sie davon ausgehen, dass 5 in 99-mal 19-mal geht. 99 ÷ 5 = 19 R 4 — jetzt erstellen wir einfach die gemischte Zahl wie zuvor. 99/5 = 19 4/5 
6/6 – sechs geht einmal in sechs, natürlich ohne Pause. 6 6 = 1 R0. Da ein Bruch mit 0 im Zähler immer gleich Null ist, müssen wir keinen Bruch neben unsere ganze Zahl setzen. 6/6 = 1 
18/6 — da wir wissen, dass 18 nur 6 × 3 ist, wissen wir, dass wir einen Rest von 0 haben, also müssen wir uns nicht um den Bruchteil unserer gemischten Zahl kümmern. 18/6 = 3 
-10/3 -10 ÷ 3 = -3 R1 -10/3 = -3 1/3
Umwandeln von unechten brüchen in gemischte zahlen
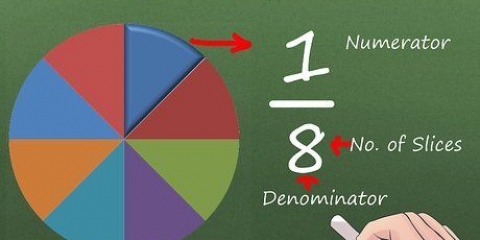
In der Mathematik sind unechte Brüche solche, bei denen der Zähler (die obere Zahl) größer oder gleich dem Nenner (die untere Zahl) ist. Um einen unechten Bruch in eine gemischte Zahl umzuwandeln (mit einem Bruch und einer ganzen Zahl, z. B. 2 3/4), dividiere den Zähler durch den Nenner. Schreibe den ganzen Teil der Antwort neben einen Bruch, mit dem Rest im Zähler und dem ursprünglichen Nenner darunter – du hast jetzt einen gemischten Bruch!
Schritte
Methode 1 von 2: Einen unechten Bruch umwandeln

1. Dividiere den Zähler durch den Nenner. Schreibe deinen unechten Bruch auf. Dann den Zähler durch den Nenner dividieren, also die Divisionssumme wie gezeigt berechnen. Vergiss nicht, den Rest aufzuschreiben.
- Nehmen wir ein Beispiel. Nehmen wir an, wir müssen den Bruch 7/5 in eine gemischte Zahl umwandeln. Wir teilen zuerst 7 durch 5, wie zum Beispiel:
- 7/5 → 7 ÷ 5 = 1 R2

2. Schreibe die ganze Zahl der Antwort. Die ganze Zahl deiner gemischten Zahl (die große Zahl links von deinem Bruch) ist die Antwort auf die ganze Zahl der Divisionssumme. Mit anderen Worten, schreiben Sie einfach die Divisionsantwort ohne den Rest.

3. Bilden Sie einen Bruch aus dem Rest und dem ursprünglichen Nenner. Jetzt müssen wir den Bruchteil der gemischten Zahl finden. Setzen Sie den Rest der Division in den Zähler ein und verwenden Sie den gleichen Nenner Ihres ursprünglichen unechten Bruchs. Setze diesen Bruch neben deine ganze Zahl und du hast deine gemischte Zahl!

4. Um dies wieder zu einem unechten Bruch zu machen, addieren wir die ganze Zahl zum Zähler. Gemischte Zahlen sehen auf dem Papier gut aus und sind gut lesbar, sind aber nicht immer die beste Wahl. Wenn wir zum Beispiel einen Bruch mit einer gemischten Zahl multiplizieren, wird unsere Arbeit viel einfacher, wenn wir die gemischte Zahl wieder in einen unechten Bruch umwandeln. Sie tun dies, indem Sie einfach die ganze Zahl mit dem Nenner multiplizieren und zum Zähler addieren.
Methode 2 von 2: Probenprobleme lösen

1. Wandeln Sie 11/4 in eine gemischte Zahl um. Dieses Problem ist einfach – lösen Sie es einfach genau wie oben. Siehe unten für eine Schritt-für-Schritt-Lösung.
- 11/4 — um zu beginnen, müssen wir den Zähler durch den Nenner dividieren.
- 11 ÷ 4 = 2 R 3 — jetzt müssen wir einen Bruchteil des Restes und unseren ursprünglichen Nenner machen.
- 11/4 = 2 3/4

2. Wandle 99/5 in eine gemischte Zahl um. Wir haben es hier mit einem sehr großen Zähler zu tun, aber lassen Sie sich davon nicht täuschen – die Methode ist genau dieselbe! Siehe unten:

3. Wandeln Sie 6/6 in eine gemischte Zahl um. Bisher haben wir uns nur mit unechten Brüchen beschäftigt, bei denen der Zähler größer als der Nenner ist. Aber was passiert, wenn beide gleich sind? Siehe unten, um es herauszufinden.

4. Wandle 18/6 in eine gemischte Zahl um. Wenn der Zähler ein Vielfaches des Nenners ist, machen Sie sich keine Sorgen um den Rest – machen Sie einfach die Divisionssumme, um Ihre Antwort zu erhalten. Siehe unten.

5. Wandeln Sie -10/3 in eine gemischte Zahl um. Negative funktionieren genauso wie positive Zahlen. Siehe unten:
Tipps
- Unsachgemäße Brüche sind nicht unbedingt erforderlich falsch. Tatsächlich sind sie manchmal nützlicher als gemischte Zahlen. Wenn Sie beispielsweise zwei Brüche multiplizieren möchten, sind unechte Brüche besser, da Sie nur Zähler und Nenner miteinander multiplizieren müssen, um Ihre Antwort zu erhalten: z. 1/6 × 7/2 = 7/12. Jetzt 1/6 × 3 1/2 multiplizieren – nicht wirklich einfach.
- Andererseits sind gemischte Zahlen normalerweise am nützlichsten, um etwas im wirklichen Leben zu beschreiben. Zum Beispiel verlangt ein Rezept 4 1/2 Tassen Mehl, nicht 9/2 Tassen Mehl.
"Umwandeln von unechten brüchen in gemischte zahlen"
Оцените, пожалуйста статью