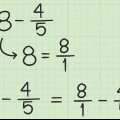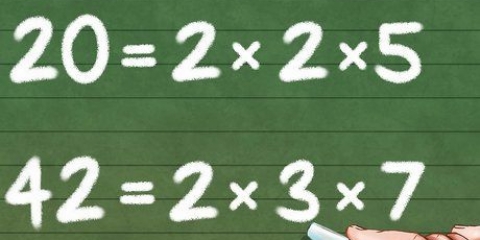Zahlen subtrahieren

Schritte
Tipps
Warnungen

Subtraktionen sind die Summen, bei denen Sie zwei Zahlen voneinander subtrahieren. Es ist ziemlich einfach, wenn Sie ganze Zahlen voneinander subtrahieren möchten, aber etwas komplizierter wird es, wenn Sie mit Brüchen oder Dezimalzahlen arbeiten. Sobald Sie die Subtraktion beherrschen, können Sie zu den komplizierteren mathematischen Konzepten übergehen und das Addieren, Multiplizieren und Dividieren von Zahlen wird viel einfacher sein.

Schritte

Methode 1 von 6: Subtrahiere große ganze Zahlen durch Ausleihen

1. Schreibe die größere Zahl auf. Angenommen, Sie arbeiten mit der Summe 32 - 17. Schreibe zuerst 32 auf.

2. Schreibe die kleinere Zahl direkt darunter. Stellen Sie sicher, dass die Zehner und Einer ordentlich aufgereiht sind, so dass die 3 Zoll "32" direkt über 1 Zoll "17" Zustand, und die 2 in "32" direkt über dem "7" bei 17.

3. Subtrahiere die untere Zahl von der oberen. Das kann etwas knifflig werden, wenn die untere Zahl größer als die obere ist. In diesem Fall ist 7 größer als 2. Hier ist, was zu tun ist:

du wirst müssen "verleihen" der 3 in "32" um die 2 zu 12 . zu machen.

Überqueren Sie die 3 von "32" und mache daraus eine 2, dann mache die Einheit 2 zu einer 12.

Jetzt hast du 12 – 7 = 5. Schreibe eine 5 unter die Einheitenspalte.

4. Subtrahiere die Zehn in der unteren Zahl von der Zehn in der oberen Zahl. Vergessen Sie nicht, dass die 3 von 32 zu einer 2 geworden ist. Ziehe nun die 1 in 17 von der 2 darüber ab, also 2-1 = 1. Schreibe 1 unter die Zehnerspalte. Wenn alles gut ist, hast du jetzt 15 als Antwort, also 32 - 17 = 15.

5. Überprüfe deine Arbeit. Wenn Sie sicherstellen möchten, dass Sie die Berechnung richtig durchgeführt haben, müssen Sie nur die Antwort zur kleinsten Zahl addieren, um die größte Zahl zurückzubekommen. Zur Überprüfung: 15 + 17 = 32, also hast du es richtig gemacht. Exzellent!

Methode 2 von 6: Subtrahiere kleine ganze Zahlen

1. Bestimme, welche Zahl größer ist. Eine Übung wie 15 - 9 erfordert einen anderen Ansatz als 2 - 30.

In der Summe 15 - 9 ist die erste Zahl, 15, die größte.
In der Summe 2 - 30 ist die zweite Zahl, 30 ist die größte.

2. Entscheide, ob deine Antwort positiv oder negativ sein soll. Wenn die erste Zahl die größte ist, ist die Antwort positiv. Wenn die zweite Zahl die größte ist, ist die Antwort negativ.

In der ersten Summe, 15 - 9, wird die Antwort also positiv, da 15 größer als 9 ist.

In der zweiten Summe, 2 - 30, wird die Antwort also negativ, weil 2 kleiner als 30 ist.

3. Finde den Unterschied zwischen den beiden Zahlen. Um zwei Zahlen zu subtrahieren, berechne die Differenz zwischen ihnen.

Für die Aufgabe 15 - 9 nimm 15 Münzen. Entferne 9 und zähle, wie viele noch übrig sind (6). Also, 15 - 9 = 6. Oder verwenden Sie einen Zahlenstrahl und zeichnen Sie die Zahlen 1 bis 15 entlang der Linie, dann streichen Sie 9 von 15 nach unten, um zu 6 zu gelangen.

Bei der Summe 2 – 30 ist es einfacher, die Zahlen umzudrehen und die Antwort negativ zu machen. Also, 30 - 2 = 28, und damit ist 2 - 30 -28.

Methode 3 von 6: Dezimalstellen subtrahieren

1. Schreiben Sie die größere Zahl über die kleinere Zahl, damit die Dezimalstellen ausgerichtet sind. Angenommen, Sie haben das folgende Problem: 10.5 - 8.3. Schreiben Sie 10.5 über 8.3 so, dass die Kommas übereinander stehen.

Wenn Sie ein Problem haben, bei dem eine Zahl mehr Dezimalstellen hat als die andere, füllen Sie das leere Feld mit Nullen. Wenn Sie beispielsweise das Problem 5.32 - 4.2 haben, können Sie es umschreiben als 5.32 = 4.20. Dadurch ändert sich der Wert einer Zahl nicht, du stellst aber sicher, dass sich beide Zahlen leichter voneinander subtrahieren lassen.

2. Subtrahiere die Zehntel voneinander. Die Subtraktion von diesen Zahlen ist die gleiche wie bei den ganzen Zahlen, außer dass Sie auf den Dezimalpunkt achten müssen, ausgerichtet und in der Antwort enthalten sind. In diesem Fall müssen Sie 3 von 5 subtrahieren. 5 - 3 = 2, also schreibst du eine 2 unter die 3 in 8.3.

Vergessen Sie nicht, das Komma (das Komma) in die Antwort aufzunehmen. Es sieht jetzt so aus: ,2.

3. Ziehe nun die Einheiten voneinander ab. Subtrahiere nun 8 von 0. Leihen Sie sich ein Dutzend der 1 (neben der 0) aus, um 10 zu erhalten, ziehen Sie jetzt 8 von 10 ab. Sie können auch sofort die Summe 10 – 8 = 2 berechnen, ohne den Zwischenschritt des Ausleihens, da die unterste Zahl keine Zehn hat. Schreiben Sie die Antwort unter 8.

4. Die endgültige Antwort lautet also 2,2.

Methode 4 von 6: Brüche subtrahieren

1. Setze Zähler und Nenner zusammen. Angenommen, Sie arbeiten mit dem Problem 13/10 - 3/5. Schreiben Sie diese Aufgabe so, dass beide Zähler 13 und 3 und beide Nenner 10 und 5 nebeneinander stehen, getrennt durch ein Minuszeichen. Das verschafft Ihnen einen besseren Überblick über das Problem und erleichtert die Lösungsfindung.

2. Finde das kleinste gemeinsame Vielfache. Dies ist das kleinste Vielfache von zwei Zahlen. Der LCF von 10 und 5 in diesem Beispiel beträgt 10.

Beachten Sie, dass der lcm von zwei Zahlen nicht immer eine der beiden Zahlen ist. Bei 3 und 2 ist der LCF beispielsweise 6, weil es keine Zahl kleiner als 6 gibt, die ein Vielfaches jeder der Zahlen ist.

3. Schreibe die Brüche mit dem gleichen Nenner um. Der Bruch 13/10 kann unverändert bleiben, weil sich der Nenner nicht geändert hat, aber der Bruch 3/5 wird gleich 6/10, weil der Nenner zweimal in das gemeinsame Vielfache von 10 . geht. Jetzt hast du beide Brüche ausgeglichen. 3/5 ist gleich 6/10, aber mit dem Unterschied, dass es jetzt kein Problem mehr ist, beide Brüche voneinander zu subtrahieren.

Die neue Aufgabe wird also sein: 13/10 - 6/10.

4. Subtrahiere beide Zähler voneinander. Also 13 - 6 = 7. Ziehe nicht die Nenner ab.

5. Platziere den neuen Zähler über dem neuen Nenner (dem zuvor berechneten LCF) für die endgültige Antwort. Der neue Zähler ist 7 und der Nenner beider Brüche ist 10. Die endgültige Antwort lautet also 7/10.

6. Überprüfe deine Arbeit. Wenn Sie sicherstellen möchten, dass Sie die Berechnung richtig durchgeführt haben, müssen Sie nur die Antwort zur kleinsten Zahl addieren, um die größte Zahl zurückzubekommen. Also um zu überprüfen: 7/10 + 6/10 = 13/10. Du bist jetzt fertig.

Methode 5 von 6: Subtrahiere einen Bruch von einer ganzen Zahl

1. Schreibe die Aufgabe. Angenommen, wir haben das folgende Problem: 5 - 3/4. Beachten Sie dies.

2. Wandle die ganze Zahl in einen Bruch mit dem gleichen Nenner wie der gegebene Bruch um. Bilden Sie einen Bruch der 5 mit dem Nenner 4. Betrachten Sie zunächst, dass 5 gleich dem Bruch 5/1 . ist. Dann multipliziert man Zähler und Nenner des neuen Bruchs mit 4, um zwei Brüche mit dem gleichen Nenner zu erhalten. Dadurch bleibt der Wert des Bruchs gleich, aber mit unterschiedlichen Zahlen. Also, 5/1 x 4/4 = 20/4.

3. Schreibe die Aufgabe um. Dies kann jetzt geschrieben werden als: 20/4 - 3/4.

4. Subtrahiere die Zähler der Brüche und halte die Brüche gleich. Also, 20 - 3 = 17. Der letzte Zähler wird also 17 und der Nenner ist 4.

5. Die Antwort auf das Problem lautet also 17/4. Um diesen unechten Bruch in einen zusammengesetzten Bruch umzuwandeln, dividiere 17 durch 4, um die Zahl 4 mit einem Rest von 1 . zu erhalten. Die Antwort sieht dann so aus: 4 1/4.

Methode 6 von 6: Subtrahieren von Variablen

1. Schreibe die Aufgabe. Angenommen, Sie arbeiten an folgendem Problem: 3x - 5x + 2y - z - (2x + 2x + y). Schreiben Sie die erste Gleichung über die zweite.

2. Subtrahiere alle gleichen Terme voneinander. Wenn Sie mit Variablen arbeiten, können Sie nur Terme mit derselben Variablen subtrahieren und mit der gleichen Macht. Dies bedeutet, dass Sie 4x -7x tun können, aber nicht 4x -7x. Sie können diese Aufgabe also wie folgt aufteilen:

3x - 2x = x

-5x - 2x = -7x

2y - y = y

-z - 0 = -z

3. Gib deine letzte Antwort. Nachdem Sie nun alle gleichen Terme abgezogen haben, können Sie sofort Ihre endgültige Antwort geben. Hier ist die Antwort:

3x - 5x + 2y - z - (2x + 2x + y) = x - 7x + y - z

Tipps

Brechen Sie größere Zahlen in kleinere Stücke auf. Nehmen: 63 - 25.Niemand sagt, dass man alle 25 auf einmal subtrahieren muss. Sie können zuerst 3 subtrahieren, um 60 zu erhalten; dann subtrahiere 20 um 40 zu erhalten und dann die letzten 2. Ergebnis: 38. Und jetzt musst du dir nichts ausleihen.

Warnungen

Wenn Sie eine Mischung aus positiven und negativen Zahlen haben, wird es viel schwieriger.Suchen Sie weiter nach Artikeln, die Ihnen dabei helfen können.