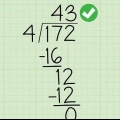
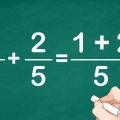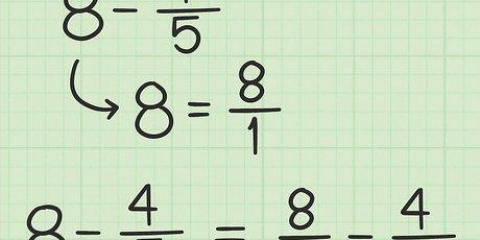1 - 0 = 1 11 - 10 = 1 1011 - 10 = 1001 
110 - 101 = ? 
Streichen Sie zuerst die 1 durch und ersetzen Sie sie durch eine 0, und Sie erhalten: 110 - 101 = ? Sie haben 10 von der ersten Zahl abgezogen, damit Sie diese "geliehene" Zahl zur Zahl in den Einheiten hinzufügen können: 110 - 101 = ? 
110 - 101 = ? Die Spalte ganz rechts ist jetzt:- 1 = 1. Wenn Sie nicht wissen, wie Sie zu dieser Antwort kommen, versuchen Sie es mit dem Problem als Dezimalzahlen berechnen: 102 = (1 x 2) + (0 x 1) = 210. (Der unter Zahlen geben an, in welcher Basis die Zahl geschrieben ist.) 12 = (1x1) = 110. In dezimaler Form sieht diese Aussage also so aus: 2 - 1 = ?, die Antwort ist also 1. 
110 - 101 = __1 = _01 = 001 = 1. 
11000 - 111 = 1110000 - 111 = (denken Sie daran, 10 - 1 = 1) 111001000 - 111 = Hier ist es etwas kürzer: 10110 - 111 = Pro Spalte lösen: _ _ _ _ 1 = _ _ _ 0 1 = _ _ 0 0 1 = _ 0 0 0 1 = 1 0 0 0 1 
Addiere die Binärzahlen zusammen um deine Arbeit zu überprüfen. Fügen Sie die Antwort zur kleineren Antwort hinzu, und Sie sollten die größere Zahl als Ergebnis erhalten. In unserem vorherigen Beispiel (11000 - 111 = 10001) erhalten wir 10001 + 111 = 11000, das ist die größere Zahl, mit der wir begonnen haben. Eine andere Möglichkeit ist Wandeln Sie eine beliebige Zahl von binär in dezimal um um zu sehen ob es richtig ist. Mit dem gleichen Beispiel (11000 - 111 = 10001) können wir jede Zahl in eine Dezimalzahl umwandeln, dann erhalten wir 24 - 7 = 17 als Antwort. Das ist richtig, also ist unsere Lösung richtig. 

101 - 011 = ? 
Im Grunde genommen nehmen wir hier das Komplement von Eins oder subtrahieren jede Ziffer im Term von Eins. Dies gilt für Binärzahlen, da es beim Vertauschen des Termes nur zwei mögliche Ergebnisse gibt: 1 - 0 = 1 und 1 - 1 = 0. 

101 + 101 = 1010 Wenn Ihnen dies unklar ist, lesen Sie mehr über Binärzahlen addieren. 
1010 = 10Daher: 101 - 011 = 10 Wenn überhaupt keine zusätzliche Ziffer, haben Sie versucht, eine größere Zahl von einer kleineren zu subtrahieren. Lesen Sie den Abschnitt Tipps zur Lösung solcher Probleme und beginnen Sie von vorne. 
56 - 17 Da wir Dezimalzahlen verwenden, nehmen wir das `Komplement von neun` des zweiten Termes (17), indem wir jede Ziffer von neun subtrahieren. 99 - 17 = 82. Machen Sie eine Summe daraus: 56 + 82. Wenn Sie dies mit dem ursprünglichen Problem (56-17) vergleichen, werden Sie feststellen, dass wir 99 . hinzugefügt haben. 56 + 82 = 138. Aber da unsere Änderungen 99 zum ursprünglichen Problem hinzugefügt haben, müssen wir 99 von der Antwort abziehen. Auch hier verwenden wir einen schnelleren Weg, genau wie bei der binären Methode oben: Addiere 1 zur Gesamtzahl und entferne dann die Ziffer links (die 100 darstellt): 138 + 1 = 139 → 139 → 39 Dies ist letztendlich die Lösung für unser ursprüngliches Problem, 56-17.
Subtrahieren von binärzahlen
Das Subtrahieren von Binärzahlen ist bei Dezimalzahlen etwas anders, aber wenn Sie die folgenden Schritte ausführen, ist es genauso einfach, wenn nicht sogar einfacher.
Schritte
Methode 1 von 2: Kredit aufnehmen

1. Platziere die Binärzahlen untereinander, genau wie bei einer normalen Minussumme. Schreibe die größere Zahl über die kleinere Zahl. Wenn die kleinere Zahl weniger Stellen hat, richten Sie beide Zahlen rechts aus, wie bei einer Dezimalzahl (Basis zehn).

2. Probieren Sie einige einfache Übungen aus. Bei einigen Binärzahlen ist die Subtraktion nicht anders als bei Dezimalzahlen. Lege die Zahlen untereinander, beginne rechts und bestimme das Ergebnis für jede Zahl. Hier ein paar einfache Beispiele:

3. Mach jetzt ein komplizierteres Problem. Sie müssen nur eine spezielle `Regel` kennen, um eine Minussumme mit Binärzahlen bilden zu können. Diese Regel sagt Ihnen, wie Sie von der Zahl links `ausleihen`, um eine `0 - 1`-Spalte zu lösen. Für den Rest dieses Teils nehmen wir ein paar Beispielprobleme und lösen sie durch Ausleihen. Hier ist der erste:

4. `Ausleihen` von der zweiten Ziffer. Aus der rechten Spalte (die Einheiten) müssen wir das Problem `0 - 1` lösen. Um dies zu tun, müssen wir von der Ziffer links davon `borgen` (die Paare). Dies geschieht in zwei Schritten:

5. Für die ganz rechte Spalte auflösen. Jetzt kann jede Spalte wie gewohnt gelöst werden. Die Spalte ganz rechts (die der Einheiten) dieses Problems können Sie wie folgt lösen:

6. Erledige die Aufgabe. Der Rest des Problems kann jetzt einfach gelöst werden. Lösen Sie es Spalte für Spalte von rechts nach links auf:

7. Versuchen Sie es mit einer schwierigeren Aufgabe. Ausleihen sind im Binärformat üblich, und manchmal müssen Sie mehrmals pro Spalte ausleihen. Wir lösen zum Beispiel folgendes: 11000 -111. Wir können uns nicht von einer 0 "ausleihen", also leihen wir uns weiter von der Ziffer auf der linken Seite, bis es etwas wird, von dem wir uns ausleihen können:

8. Überprüfe deine Antwort. Es gibt immer drei Möglichkeiten, Ihre Antwort zu überprüfen. Eine schnelle Möglichkeit besteht darin, das Problem in a . einzugeben Binärrechner online. Die anderen beiden Methoden sind weiterhin nützlich, da Sie möglicherweise Ihre Antwort während eines Tests von Hand überprüfen müssen und Ihnen den Umgang mit Binärzahlen erleichtern:
Methode 2 von 2: Verwenden der Komplementmethode

1. Richten Sie die beiden Zahlen wie bei der Dezimalsubtraktion aus. Diese Methode wird von Computern zum Subtrahieren von Binärzahlen verwendet, da sie ein effizienteres Programm verwendet. Für jemanden, der es gewohnt ist, gängige Dezimalzahlen zu subtrahieren, ist dies wahrscheinlich eine schwierigere Methode, kann aber für einen Programmierer nützlich sein, um es zu verstehen.
- Wir verwenden das folgende Beispiel: 101 - 11 = ?

2. Setzen Sie ggf. Nullen davor, damit beide Zahlen gleich viele Stellen haben. Konvertieren Sie beispielsweise 101-11 in 101-011, sodass beide Zahlen dreistellig sind.

3. Vertausche die Zahlen im zweiten Term. Mache im zweiten Term alle Nullen zu Einsen und alle Einsen zu Nullen. In unserem Beispiel wird der zweite Term zu: 011 → 100.

4.Füge eins zum neuen zweiten Term hinzu. Sobald Sie den `inversen` Term haben, fügen Sie einen zum Ergebnis hinzu. In unserem Beispiel erhalten wir 100 + 1 = 101.

5.Löse das neue Problem als binäre Addition. Verwenden Sie binäre Additionstechniken, um den neuen Term zum ursprünglichen Term hinzuzufügen, anstatt ihn zu subtrahieren:

6. Ignoriere die erste Ziffer. Bei dieser Methode bekommt man am Ende immer eine Antwort, die eine Ziffer zu lang ist. Zum Beispiel haben wir mit Zahlen von jeweils drei Ziffern (101 + 101) angefangen, aber mit einer vierstelligen Antwort (1010) geendet. Streichen Sie die erste Ziffer durch und Sie erhalten die Antwort auf das Original minus summe:

7. Versuchen Sie diese Methode mit Dezimalzahlen. Diese Methode heißt die "2er Komplement"-Methode, weil die Schritte mit der `Zahlen umkehren` das `1er-Komplement` ergeben, wonach 1 addiert wird. Um besser zu verstehen, warum diese Methode funktioniert, versuchen Sie es im Dezimalzahlensystem (Basis 10):
Tipps
- Um eine größere Zahl von einer kleineren Zahl zu subtrahieren, kehre die Reihenfolge der Zahlen um, berechne die Minussumme und füge der Antwort ein Minuszeichen hinzu. Um beispielsweise nach der Binärsumme 11-100 aufzulösen, würden wir zuerst 100-11 berechnen und dann der Antwort ein Minuszeichen hinzufügen (und diese Regel gilt für die Subtraktion in jeder Basis, nicht nur für Binärzahlen).
- Mathematisch verwendet die Komplementmethode die Identität a - b = a + (2 - b) - 2 Wenn n die Anzahl der Stellen in b ist, dann ist 2 - b eins mehr als das Ergebnis des Durchstreichens.
"Subtrahieren von binärzahlen"
Оцените, пожалуйста статью