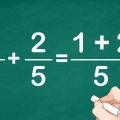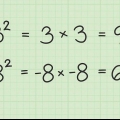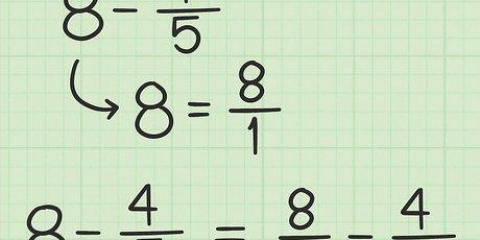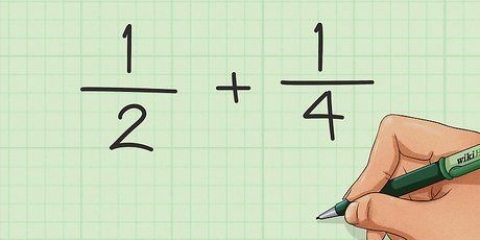30√2 - 4√2 + 10√3 = (30 - 4)√2 + 10√3 = 26√2 + 10√3 

Vereinfachen 6√(40). Zuerst können Sie `40` in `4 x 10` auflösen, und Sie erhalten 6√(40) = 6√(4×10). Dann berechnen Sie `2` aus dem Quadrat `4` und multiplizieren dies mit dem aktuellen Koeffizienten. Jetzt hast du 6√(4×10) = (6 x 2)√10. Multiplizieren Sie die beiden Koeffizienten und Sie erhalten 12√10`.` Die Aufgabe lautet nun wie folgt: 12√10 - 3√(10) + √5. Da die ersten beiden Terme dieselbe Wurzel haben, können Sie den zweiten Term vom ersten subtrahieren und den dritten so lassen, wie er ist. du liebst jetzt (12-3)√10 + √5 über, was vereinfacht werden kann zu 9√10 + √5. 

Denn 9 gleich (3x3), kannst du das vereinfachen: 9 wird 3. Denn 4 gleich (2x2), kannst du das vereinfachen: 4 wird 2. Nun ist die Summe 3 + 2 = 5. Denn 5 und 3√2 sind nicht gleichbedeutend, da ist jetzt nichts mehr zu tun. Ihre letzte Antwort ist 5 - 3√2. 
Stellen Sie sicher, dass diese Begriffe denselben Nenner haben. Der kleinste gemeinsame Nenner oder der durch `4` und `2` teilbare Nenner ist `4`. Um den zweiten Term ((√2)/2) mit einem Nenner 4 zu bilden, müssen Sie also sowohl den Zähler als auch den Nenner mit 2/2 multiplizieren. (√2)/2 x 2/2 = (2√2)/4. Addiere den Nenner der Brüche zusammen, während der Nenner gleich bleibt. Mach einfach, was du tun würdest, wenn du Brüche addieren würdest. (√2)/4 + (2√2)/4 = 3√2)/4`.`
Quadratwurzeln addieren und subtrahieren
Um Quadratwurzeln zu addieren und zu subtrahieren, müssen Sie Quadratwurzeln mit derselben Wurzel kombinieren. Dies bedeutet, dass Sie 2√3 zu 4√3 addieren (oder subtrahieren) können, aber Sie können 2√3 und 2√5 . nicht addieren. Es gibt viele Fälle, in denen Sie die Zahl unter dem Wurzelzeichen vereinfachen können, um gleiche Terme kombinieren und Quadratwurzeln frei addieren und subtrahieren zu können.
Schritte
Teil 1 von 2: Die Grundlagen beherrschen

1. Vereinfachen Sie die Terme unter den Radikalen, wenn möglich. Um die Terme unter den Radikalen zu vereinfachen, versuchen Sie, sie in mindestens ein perfektes Quadrat zu zerlegen, z. B. 25 (5 x 5) oder 9 (3 x 3). Sobald Sie dies getan haben, können Sie die Quadratwurzel des perfekten Quadrats ziehen und sie außerhalb der Radikale platzieren, wobei der verbleibende Faktor unterhalb der Radikale bleibt. In diesem Beispiel gehen wir vom Problem aus 6√50 - 2√8 + 5√12. Die Zahlen außerhalb des Radikals sind die Koeffizienten und die Zahlen darunter nennen wir die Wurzelzahlen. So vereinfachen Sie die Begriffe:
- 6√50 = 6√(25 x 2) = (6 x 5)√2 = 30√2. Sie haben `50` in `25 x 2` aufgelöst und dann `5` außerhalb der Wurzel (der Wurzel von `25`) platziert, danach bleibt `2` unter dem Radikal. Dann multipliziert man `5` mit `6`, der Zahl, die bereits außerhalb des Radikals lag, und erhält 30 als neuen Koeffizienten.
- 2√8 = 2√(4 x 2) = (2 x 2)√2 = 4√2. Hier haben Sie `8` in `4 x 2` faktorisiert und dann die Quadratwurzel von 4 abgezogen, so dass Sie eine `2` außerhalb des Radikals und eine `2` unterhalb des Radikals haben. Dann multipliziert man `2` mit `2`, der Zahl, die bereits außerhalb des Radikals lag, und erhält 4 als neuen Koeffizienten.
- 5√12 = 5√(4 x 3) = (5 x 2)√3 = 10√3. Hier haben Sie `12` in `4 x 3` faktorisiert und dann die Quadratwurzel von 4 abgezogen, so dass Sie eine `2` außerhalb des Radikals und eine `3` unterhalb des Radikals haben. Dann multipliziert man `2` mit `5`, der Zahl, die bereits außerhalb des Radikals lag, und man erhält 10 als neuen Koeffizienten.

2. Kreise alle Terme mit entsprechenden Wurzelzahlen ein. Nachdem Sie die Wurzelzahlen der angegebenen Terme vereinfacht haben, bleibt die folgende Gleichung übrig: 30√2 - 4√2 + 10√3. Da Sie nur wie Wurzeln addieren oder subtrahieren können, müssen Sie diese Begriffe mit derselben Wurzel einkreisen, in diesem Beispiel: 30√2 und 4√2. Sie können dies mit dem Addieren oder Subtrahieren von Brüchen vergleichen, bei denen Sie die Terme nur addieren oder subtrahieren können, wenn die Nenner gleich sind.

3. Wenn Sie mit einer längeren Gleichung arbeiten und mehrere Paare übereinstimmender Wurzelzahlen vorhanden sind, können Sie das erste Paar einkreisen, das zweite unterstreichen, das dritte mit einem Sternchen versehen usw. Wenn Sie ähnliche Begriffe in eine Reihenfolge bringen, können Sie sich die Lösung leichter vorstellen.

4. Berechnen Sie die Summe der Koeffizienten der Terme mit gleichen Wurzeln. Jetzt müssen Sie nur noch die Summe der Koeffizienten der Terme mit gleichen Wurzeln berechnen und die anderen Terme der Gleichung ignorieren. Die Wurzelzahlen bleiben unverändert. Die Idee ist, dass Sie angeben, wie viele dieser Wurzelzahlen es insgesamt gibt. Die nicht übereinstimmenden Begriffe können so bleiben, wie sie sind. Hier ist, was Sie tun:
Teil 2 von 2: Mehr Bewegung

1. Machen Sie Beispiel 1. In diesem Beispiel addieren Sie die folgenden Quadratwurzeln: √(45) + 4√5. Sie müssen Folgendes tun:
- Vereinfachen (45). Zuerst kannst du es so lösen (9 x 5).
- Dann nimmst du die Quadratwurzel aus Neun und erhältst `3`, die du dann außerhalb der Quadratwurzel platzierst. So, (45) = 3√5.
- Addiere nun die Koeffizienten der beiden Terme mit übereinstimmenden Wurzeln, um deine Antwort zu erhalten. 3√5 + 4√5 = 7√5

2. Machen Sie Beispiel 2. Das folgende Beispiel ist diese Zuordnung: 6√(40) - 3√(10) + √5. Sie müssen Folgendes tun, um dies zu beheben:
3. Machen Sie Beispiel 3. Dieses Beispiel geht so: 9√5 -2√3 - 4√5. Keine der Wurzeln enthält ein Quadrat, daher ist keine Vereinfachung möglich. Der erste und der dritte Term haben gleiche Wurzeln, daher können ihre Koeffizienten subtrahiert werden (9 - 4). Die Wurzelzahl bleibt gleich. Die restlichen Terme sind nicht gleich, daher kann das Problem vereinfacht werden zu5√5 - 2√3`.`


4. Machen Sie Beispiel 4. Angenommen, Sie haben mit folgendem Problem zu tun: √9 + √4 - 3√2 Sie müssen nun Folgendes tun:

5. Machen Sie Beispiel 5. Versuchen wir, die Summe der Quadratwurzeln zu ziehen, die Teil eines Bruchs sind. Genau wie bei einem regulären Bruch können Sie jetzt nur noch die Summe von Brüchen mit demselben Zähler oder Nenner berechnen. Angenommen, Sie arbeiten mit diesem Problem: (√2)/4 + (√2)/2, Gehen Sie nun wie folgt vor:
Tipps
- Wurzelzahlen mit einem Quadrat als Faktor sollten immer vereinfacht werden Pro du wirst gleiche Wurzelzahlen bestimmen und kombinieren.
Warnungen
- Sie können niemals ungleiche Wurzelzahlen kombinieren.
- Du kannst niemals eine ganze Zahl und eine Quadratwurzel kombinieren. So: 3 + (2x) kann nicht vereinfacht werden.
- Anmerkung: `(2x) ist dasselbe wie `(√(2x)`.
"Quadratwurzeln addieren und subtrahieren"
Оцените, пожалуйста статью