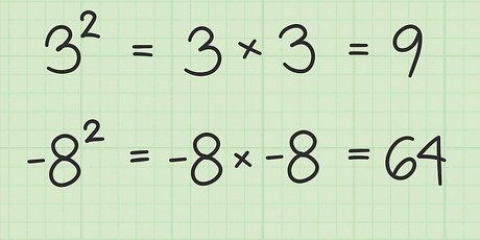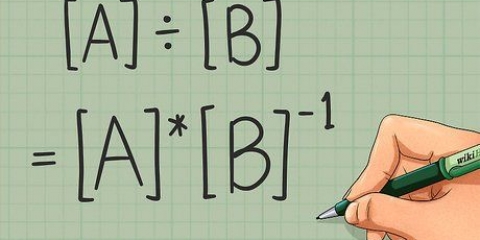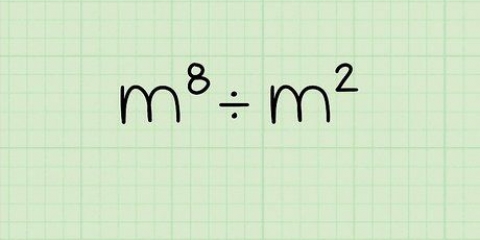Quadratwurzeln teilen

Schritte
Tipps
Warnungen

Das Dividieren durch Quadratwurzeln ist im Wesentlichen die Vereinfachung eines Bruchs. Natürlich macht das Vorhandensein von Quadratwurzeln den Prozess etwas komplizierter, aber es gibt Regeln, die es uns ermöglichen, auf relativ einfache Weise mit Brüchen zu arbeiten. Das Wichtigste ist, dass Sie Koeffizienten durch Koeffizienten und Wurzeln durch Wurzeln dividieren müssen. Du solltest auch niemals eine Quadratwurzel in einem Nenner belassen.

Schritte

Methode 1 von 4: Karotten teilen

1. Stelle den Bruch auf. Wenn der Ausdruck nicht bereits die Form eines Bruchs hat, schreiben Sie ihn so um. Dies macht es einfacher, alle notwendigen Schritte zum Dividieren durch eine Quadratwurzel zu befolgen. Denken Sie daran, dass ein Divisionszeichen mit einem Bruchstrich identisch ist.

Zum Beispiel, wenn Sie $\sqrt{144} \div \sqrt{36}$ ${sqrt{144}}div {sqrt{36}}$ berechnet, dann schreiben Sie das Problem um als: $\frac{\sqrt{144}}{\sqrt{36}}$ ${frac{{sqrt{144}}}{{sqrt{36}}}}$ .

2. Verwenden Sie ein radikales Zeichen. Wenn Ihr Problem eine Quadratwurzel im Zähler und Nenner hat, können Sie beide Wurzeln unter ein Radikal setzen. (Eine Wurzel ist die Zahl unter dem Radikal.) So wird das Vereinfachen noch einfacher.

Zum Beispiel,

\frac{\sqrt{144}}{\sqrt{36}}

${frac{{sqrt{144}}}{{sqrt{36}}}}$ kann umgeschrieben werden als

\sqrt{\frac{144}{36}}

${sqrt{{frac{144}{36}}}}$ .

3. Teile die Wurzeln. Teilen Sie die Zahlen wie jede ganze Zahl. Stellen Sie sicher, dass der Quotient unter einem neuen Radikal steht.

Zum Beispiel,

\frac{144}{36} = 4

${frac{144}{36}}=4$ , So

\sqrt{\frac{144}{36}} = \sqrt{4}

${sqrt{{frac{144}{36}}}}={sqrt{4}}$ .

4. Vereinfachen, Falls benötigt. Wenn die Wurzelzahl ein Quadrat ist oder einer der Faktoren ein perfektes Quadrat ist, müssen Sie den Ausdruck vereinfachen. Ein Quadrat oder perfektes Quadrat ist das Produkt einer ganzen Zahl mit sich selbst multipliziert. 25 ist zum Beispiel ein perfektes Quadrat, weil

5 \times 5 = 25

$5mal 5=25$ .

Zum Beispiel ist 4 ein perfektes Quadrat, weil

2 \times 2 = 4

$2mal 2=4$ . Daher:

\sqrt{4}

${sqrt{4}}$

= \sqrt{2 \times 2}

$={sqrt{2times 2}}$

= 2

$=2$
Also,

\frac{\sqrt{144}}{\sqrt{36}} = \sqrt{4} = 2

${frac{{sqrt{144}}}{{sqrt{36}}}}={sqrt{4}}=2$ .

Methode 2 von 4: Wurzeln faktorisieren

1. Drücken Sie das Problem als Bruch aus. Der Ausdruck ist wahrscheinlich schon so geschrieben. Wenn nicht, ändern Sie es. Wenn Sie einen Bruch daraus machen, können Sie die notwendigen Schritte leichter befolgen, insbesondere beim Faktorisieren von Quadratwurzeln. Denken Sie daran, dass ein Divisionszeichen mit einem Bruchstrich identisch ist.

Zum Beispiel bei der Berechnung $\sqrt{8} \div \sqrt{36}$ ${sqrt{8}}div {sqrt{36}}$ , schreibe den Ausdruck um als: $\frac{\sqrt{8}}{\sqrt{36}}$ ${frac{{sqrt{8}}}{{sqrt{36}}}}$ .

2. Zerlege jede Karotte in Faktoren. Faktoriere die Zahl wie eine ganze Zahl. Lassen Sie die Faktoren unter den radikalen Vorzeichen.

Zum Beispiel:

\frac{\sqrt{8}}{\sqrt{36}} = \frac{\sqrt{2 \times 2 \times 2}}{\sqrt{6 \times 6}}

${frac{{sqrt{8}}}{{sqrt{36}}}}={frac{{sqrt{2times 2times 2}}}{{sqrt{6times 6 }}}}$

3. Vereinfachen Sie Zähler und Nenner des Bruchs. Zu eine Quadratwurzel vereinfachen, schließen Sie alle Faktoren aus, aus denen das Produkt ein Quadrat ist?. Ein Quadrat ist das Ergebnis einer ganzen Zahl multipliziert mit sich selbst. Der Faktor wird nun zu einem Koeffizienten außerhalb der Quadratwurzel.

Zum Beispiel:

\sqrt{} 2 \times 2 \times 2 \sqrt{6 \times 6}

${frac{{sqrt{{cancel{2times 2times}}2}}}{{sqrt{{cancel{6times 6}}}}}}}$

2 \sqrt{2} 6

${frac{2{sqrt{2}}}{6}}$
Also,

\frac{\sqrt{8}}{\sqrt{36}} = 2 \sqrt{2} 6

${frac{{sqrt{8}}}{{sqrt{36}}}}={frac{2{sqrt{2}}}{6}}$

4. Streichen Sie ggf. das Wurzelzeichen aus dem Nenner. Ein Ausdruck darf in der Regel keine Quadratwurzel im Nenner haben. Wenn Ihr Bruch eine Quadratwurzel im Nenner hat, müssen Sie diese eliminieren. Das bedeutet, die Wurzel im Nenner zu entfernen. Multiplizieren Sie dazu Zähler und Nenner des Bruchs mit der Quadratwurzel, die Sie eliminieren müssen.

Angenommen, Ihr Ausdruck ist

6 \sqrt{2} \sqrt{3}

${frac{6{sqrt{2}}}{{sqrt{3}}}}}$ , dann musst du Zähler und Nenner mit multiplizieren

\sqrt{3}

${sqrt{3}}$ um die Quadratwurzel aus dem Nenner zu entfernen:

6 \sqrt{2} \sqrt{3} \times \frac{\sqrt{3}}{\sqrt{3}}

${frac{6{sqrt{2}}}{{sqrt{3}}}}times {frac{{sqrt{3}}}{{sqrt{3}}}}$

= 6 \sqrt{2} \times \sqrt{3} \sqrt{3} \times \sqrt{3}

$={frac{6{sqrt{2}}times {sqrt{3}}}{{sqrt{3}}times {sqrt{3}}}}$

= 6 \sqrt{6} \sqrt{9}

$={frac{6{sqrt{6}}}{{sqrt{9}}}}$

= 6 \sqrt{6} 3

$={frac{6{sqrt{6}}}{3}}$ .

5. Vereinfachen Sie ggf. weiter. Manchmal bleiben Koeffizienten übrig, die weiter vereinfacht werden können, oder reduzieren. Vereinfachen Sie die ganzen Zahlen im Zähler und Nenner so, wie Sie einen Bruch vereinfachen würden.

Zum Beispiel,

\frac{2}{6}

${frac{2}{6}}$ kann reduziert werden auf

\frac{1}{3}

${frac{1}{3}}$ , So

2 \sqrt{2} 6

${frac{2{sqrt{2}}}{6}}$ kann reduziert werden auf

1 \sqrt{2} 3

${frac{1{sqrt{2}}}{3}}$ , oder einfach

\frac{\sqrt{2}}{3}

${frac{{sqrt{2}}}{3}}$ .

Methode 3 von 4: Quadratwurzeln mit Koeffizienten dividieren

1. Vereinfachen Sie die Koeffizienten. Das sind die Zahlen außerhalb des Radikals. Um sie zu vereinfachen, teile oder reduzieren, ignoriere die Quadratwurzeln vorerst.

Zum Beispiel, wenn Sie $4 \sqrt{32} 6 \sqrt{16}$ ${frac{4{sqrt{32}}}{6{sqrt{16}}}}$ berechnen musst, dann vereinfache zuerst $\frac{4}{6}$ ${frac{4}{6}}$ . Zähler und Nenner können beide durch den Faktor 2 geteilt werden. Sie können dies also vereinfachen zu: $\frac{4}{6} = \frac{2}{3}$ ${frac{4}{6}}={frac{2}{3}}$ .

2. Vereinfachen Sie die Quadratwurzeln. Wenn der Zähler durch den Nenner teilbar ist, dividiere einfach die Zahlen unter den Radikalen. Wenn nicht, vereinfachen Sie jede Quadratwurzel auf die gleiche Weise wie andere Quadratwurzeln.

Da 32 beispielsweise durch 16 teilbar ist, können Sie die Quadratwurzeln teilen:

\sqrt{\frac{32}{16}} = \sqrt{2}

${sqrt{{frac{32}{16}}}}={sqrt{2}}$ .

3. Multiplizieren Sie den/die vereinfachten Koeffizienten mit der vereinfachten Quadratwurzel. Denken Sie daran, dass es keine Quadratwurzel in einem Nenner geben kann. Wenn Sie also einen Bruch mit einer Quadratwurzel multiplizieren, setzen Sie die Quadratwurzel in den Zähler.

Zum Beispiel,

\frac{2}{3} \times \sqrt{2} = 2 \sqrt{2} 3

${frac{2}{3}}times {sqrt{2}}={frac{2{sqrt{2}}}{3}}$ .

4. Eliminieren Sie ggf. die Quadratwurzel im Nenner. Dies nennt man Rationalisierung des Nenners. Die Regel ist, dass ein Ausdruck keine Quadratwurzel im Nenner haben darf. Um die Wurzel vom Nenner zu subtrahieren, multiplizieren Sie den Zähler und den Nenner mit der Quadratwurzel, die Sie subtrahieren möchten.

Wenn Sie beispielsweise einen Ausdruck wie . haben

4 \sqrt{3} 2 \sqrt{7}

${frac{4{sqrt{3}}}{2{sqrt{7}}}}$ , dann musst du Zähler und Nenner mit multiplizieren

\sqrt{7}

${sqrt{7}}$ um die Quadratwurzel im Nenner zu eliminieren:

4 \sqrt{3} \sqrt{7} \times \frac{\sqrt{7}}{\sqrt{7}}

${frac{4{sqrt{3}}}{{sqrt{7}}}}times {frac{{sqrt{7}}}{{sqrt{7}}}}$

= 4 \sqrt{3} \times \sqrt{7} \sqrt{7} \times \sqrt{7}

$={frac{4{sqrt{3}}times {sqrt{7}}}{{sqrt{7}}times {sqrt{7}}}}$

= 4 \sqrt{21} \sqrt{49}

$={frac{4{sqrt{21}}}{{sqrt{49}}}}$

= 4 \sqrt{21} 7

$={frac{4{sqrt{21}}}{7}}$

Methode 4 von 4: Dividieren durch ein Binomial mit einer Quadratwurzel

1. Bestimme, ob du ein Binomial im Nenner hast. Der Nenner ist die Zahl in der Aufgabe, durch die Sie dividieren. Ein Binomial ist ein Polynom mit zwei Termen. Diese Methode gilt nur für die Division von Quadratwurzeln mit einem Binomial.

Zum Beispiel, wenn Sie $1 5 + \sqrt{2}$ ${frac{1}{5+{sqrt{2}}}}$ Wenn du rechnen willst, hast du ein Binomial im Nenner, denn $5 + \sqrt{2}$ $5+{sqrt{2}}$ ist ein Polynom mit zwei Termen.

2. Bestimme die Konjunktion des Binomials. Konjugierte Paare sind Binome mit den gleichen Termen, aber entgegengesetzten Operatoren. Mit einem Konjunktivpaar kannst du die Quadratwurzel aus dem Nenner eliminieren.

Zum Beispiel,

5 + \sqrt{2}

$5+{sqrt{2}}$ und

5 - \sqrt{2}

$5-{sqrt{2}}$ sind konjunktive Paare, weil sie die gleichen Terme, aber entgegengesetzte Operatoren haben.

3. Multipliziere Zähler und Nenner mit der Konjunktion des Nenners. Auf diese Weise können Sie die Quadratwurzel eliminieren, da das Produkt eines konjugierten Paares die Differenz der Quadrate jedes Termes im Binomial ist. Das ist,

(ein - B) (ein + B) = ein 2 - B^{2}

$(a-b)(a+b)=a^{{2}}-b^{{2}}$ .

Zum Beispiel:

1 5 + \sqrt{2}

${frac{1}{5+{sqrt{2}}}}$

= 1 (5 - \sqrt{2}) (5 + \sqrt{2}) (5 - \sqrt{2})

$={frac{1(5-{sqrt{2}})}{(5+{sqrt{2}})(5-{sqrt{2}})}}$

= 5 - \sqrt{2} (5 2 - (\sqrt{2})^{2}

$={frac{5-{sqrt{2}}}{(5^{{2}}-({sqrt{2}})^{{2}}}}$

= 5 + \sqrt{2} 25 - 2

$={frac{5+{sqrt{2}}}{25-2}}$

= 5 + \sqrt{2} 23

$={frac{5+{sqrt{2}}}{23}}$
daher,

1 5 + \sqrt{2} = 5 + \sqrt{2} 23

${frac{1}{5+{sqrt{2}}}}={frac{5+{sqrt{2}}}{23}}$ .

Tipps

Viele Taschenrechner haben spezielle Funktionen für Brüche. Geben Sie den Koeffizienten des Zählers ein, drücken Sie die Brüche-Taste und geben Sie dann den Koeffizienten des Nenners ein. Wenn Sie danach das Gleichheitszeichen drücken, sollte der Rechner die Koeffizienten in die kleinsten Ausdrücke umgeschrieben haben.
Im Gegensatz zum Addieren und Subtrahieren von Wurzeln ist es bei einem Bruch nicht notwendig, zuerst die Wurzeln zu vereinfachen, um die Quadrate zu entfernen. Tatsächlich ist es oft besser, dies nicht zu tun.
Wenn Sie mit Quadratwurzeln arbeiten, sind unechte Brüche einfacher zu lösen als gemischte Zahlen.

Warnungen

Setzen Sie niemals eine Dezimalzahl in einen Bruch. Das wäre sonst ein Bruch im Bruch.
Stellen Sie niemals eine dezimale oder gemischte Zahl vor eine Wurzel, wandeln Sie sie in einen Bruch um und vereinfachen Sie den gesamten Ausdruck.
Lasse niemals eine Quadratwurzel im Nenner eines Bruchs, sondern vereinfache den Bruch.
Wenn der Nenner irgendeine Form von Addition oder Subtraktion enthält, verwenden Sie die Methode der konjugierten Paare, um das Radikal vom Nenner zu entfernen.

"Quadratwurzeln teilen"

Quadratwurzeln multiplizieren

Gemischte brüche teilen

Quadratwurzeln vereinfachen

Quadratwurzeln addieren und subtrahieren

Оцените, пожалуйста статью