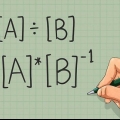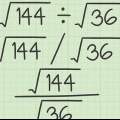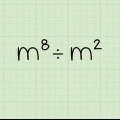Beispiel 1: Lösen Sie:  .
.
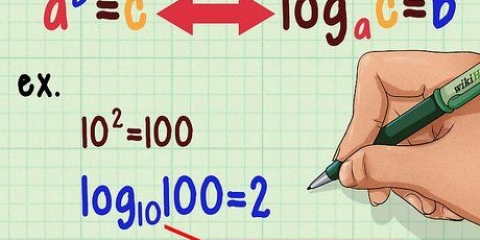
Beginnen Sie damit, dies mit der obigen Formel in einen Logarithmus umzuwandeln: .
. Diese Formel ist die `Basisänderung`-Formel, abgeleitet von den logarithmischen Grundeigenschaften. 
Beispiel 1 (Fortsetzung.): Umschreiben  wenn
wenn  . Der Wert von `?` ist die Antwort auf das Problem. Möglicherweise müssen Sie einige ausprobieren, um es zu finden:
. Der Wert von `?` ist die Antwort auf das Problem. Möglicherweise müssen Sie einige ausprobieren, um es zu finden:



16 ist das, wonach du gesucht hast, also = 4.
= 4. 
Beispiel 2: Was ist  ?
? Wandeln Sie dies in einen Logarithmus um:  .(Notiere dass der 3 verschwindet in jedem anfänglichen Log -- dies gilt für jede Basis).
.(Notiere dass der 3 verschwindet in jedem anfänglichen Log -- dies gilt für jede Basis). Umschreiben als  und teste mögliche Werte von ?:
und teste mögliche Werte von ?:


Da 58 zwischen diesen beiden Zahlen liegt, hat keine ganze Zahl als Antwort.
keine ganze Zahl als Antwort. Hinterlassen Sie Ihre Antwort als:  .
. 

Wenn entweder x oder y ist negativ, es gibt keine Lösung für das Problem. wenn beide x wenn y negativ ist, entfernen Sie die negativen Vorzeichen mit der Eigenschaft 
In der Beispielaufgabe gibt es keine Logarithmen negativer Zahlen, also können Sie mit dem nächsten Schritt fortfahren. 
Verwenden Sie dies, um die linke Seite des Beispielproblems zu erweitern:

Setze dies wieder in die ursprüngliche Gleichung ein:

→


Das Beispielproblem hat einen neuen Begriff:  . Da 3 = 27, vereinfache
. Da 3 = 27, vereinfache  böse 3.
böse 3. Der vollständige Vergleich ist jetzt:




 .
.
In der Beispielaufgabe ist die n immer noch gefangen im Begriff  .
.
Rund um die n Verwenden Sie zum Isolieren die Produktregel der Logarithmen:

Setzen Sie dies wieder in die vollständige Gleichung ein:





Seit 3 = 19683, n = 19683
Logarithmen teilen
Logarithmen mögen schwierig aussehen, aber genau wie Exponenten oder Polynome müssen Sie nur die richtigen Techniken erlernen. Sie müssen nur ein paar grundlegende Eigenschaften kennen, um zwei Logarithmen mit derselben Basis zu teilen oder einen Logarithmus um einen Quotienten zu erweitern.
Schritte
Methode 1 von 2: Logarithmen von Hand dividieren

1. Auf negative Zahlen und Einsen prüfen. Diese Methode behandelt Probleme in der Form  . In einigen Sonderfällen funktioniert es jedoch nicht:
. In einigen Sonderfällen funktioniert es jedoch nicht:
 . In einigen Sonderfällen funktioniert es jedoch nicht:
. In einigen Sonderfällen funktioniert es jedoch nicht: - Der Logarithmus einer negativen Zahl ist nicht für alle Basen definiert (wie
oder
). Dann schreibe `Keine Lösung`.
- Auch der Logarithmus von Null ist für alle Basen undefiniert. Wenn Sie einen Begriff wie sehen
, dann schreibe auch `Keine Lösung`.
- Der Logarithmus von Eins in jeder Basis (
) ist immer gleich Null, da
für alle Werte von x. Ersetzen Sie diesen Logarithmus durch 1, anstatt die folgende Methode zu verwenden.
- Wenn die beiden Logarithmen unterschiedliche Basen haben, wie z
, und Sie können keines von beiden auf eine ganze Zahl vereinfachen, dann kann das Problem nicht von Hand gelöst werden.

2. Bearbeiten Sie den Ausdruck in einem Logarithmus. Angenommen, Sie haben keine der oben genannten Ausnahmen gefunden, können Sie das Problem jetzt in einen Logarithmus vereinfachen. Verwenden Sie dazu die Formel .
.
 .
. .
.Beginnen Sie damit, dies mit der obigen Formel in einen Logarithmus umzuwandeln:
 .
.
3. Berechnen Sie dies wenn möglich von Hand. Denken Sie daran: om  zu lösen, denkst du an `
zu lösen, denkst du an ` “ oder „Welchen Exponenten kann ich verwenden? ein erhöhen auf x bekommen?` Ohne Taschenrechner ist das nicht immer zu lösen, aber wenn man Glück hat, erhält man einen leicht vereinfachten Logarithmus.
“ oder „Welchen Exponenten kann ich verwenden? ein erhöhen auf x bekommen?` Ohne Taschenrechner ist das nicht immer zu lösen, aber wenn man Glück hat, erhält man einen leicht vereinfachten Logarithmus.
 zu lösen, denkst du an `
zu lösen, denkst du an ` “ oder „Welchen Exponenten kann ich verwenden? ein erhöhen auf x bekommen?` Ohne Taschenrechner ist das nicht immer zu lösen, aber wenn man Glück hat, erhält man einen leicht vereinfachten Logarithmus.
“ oder „Welchen Exponenten kann ich verwenden? ein erhöhen auf x bekommen?` Ohne Taschenrechner ist das nicht immer zu lösen, aber wenn man Glück hat, erhält man einen leicht vereinfachten Logarithmus. wenn
wenn  . Der Wert von `?` ist die Antwort auf das Problem. Möglicherweise müssen Sie einige ausprobieren, um es zu finden:
. Der Wert von `?` ist die Antwort auf das Problem. Möglicherweise müssen Sie einige ausprobieren, um es zu finden:


16 ist das, wonach du gesucht hast, also
 = 4.
= 4.
4. Lassen Sie die Antwort in Logarithmusform, wenn Sie es nicht vereinfachen können. Manche Logarithmen sind von Hand nur sehr schwer zu lösen. Sie brauchen einen Taschenrechner, wenn Sie die Antwort für einen praktischen Zweck benötigen. Wenn Sie Probleme im Mathematikunterricht lösen, erwartet Ihr Lehrer wahrscheinlich, dass Sie die Antwort als Logarithmus hinterlassen. Hier ist ein weiteres Beispiel, das diese Methode für ein kniffligeres Problem verwendet:
 ?
? .(Notiere dass der 3 verschwindet in jedem anfänglichen Log -- dies gilt für jede Basis).
.(Notiere dass der 3 verschwindet in jedem anfänglichen Log -- dies gilt für jede Basis). und teste mögliche Werte von ?:
und teste mögliche Werte von ?:

Da 58 zwischen diesen beiden Zahlen liegt, hat
 keine ganze Zahl als Antwort.
keine ganze Zahl als Antwort. .
.Methode 2 von 2: Arbeiten mit dem Logarithmus eines Quotienten

1. Beginnen Sie mit einer Divisionsaufgabe in einem Logarithmus. Dieser Abschnitt hilft Ihnen bei der Lösung von Problemen mit Ausdrücken im Formular  .
.
 .
. - Beginnen Sie beispielsweise mit diesem Problem:
`Löse nach n auf, wenn.`

2. Auf negative Zahlen prüfen. Der Logarithmus einer negativen Zahl ist undefiniert. Wenn x oder y eine negative Zahl sind, prüfen Sie, ob es eine Lösung für das Problem gibt, bevor Sie fortfahren:


3. Teilen Sie den Quotienten in zwei Logarithmen. Eine nützliche Eigenschaft von Logarithmen wird durch die Formel beschrieben:  . Mit anderen Worten, der Logarithmus eines Quotienten ist immer gleich dem Logarithmus des Zählers abzüglich des Logarithmus des Nenners.
. Mit anderen Worten, der Logarithmus eines Quotienten ist immer gleich dem Logarithmus des Zählers abzüglich des Logarithmus des Nenners.
 . Mit anderen Worten, der Logarithmus eines Quotienten ist immer gleich dem Logarithmus des Zählers abzüglich des Logarithmus des Nenners.
. Mit anderen Worten, der Logarithmus eines Quotienten ist immer gleich dem Logarithmus des Zählers abzüglich des Logarithmus des Nenners.

→


4. Vereinfachen Sie die Logarithmen, wenn möglich. Wenn einer der neuen Logarithmen im Ausdruck eine ganze Zahl ist, vereinfachen Sie sie jetzt.
 . Da 3 = 27, vereinfache
. Da 3 = 27, vereinfache  böse 3.
böse 3.

5. Isolieren Sie die Variable. Wie bei jedem mathematischen Problem hilft es, den Term mit der Variablen auf einer Seite der Gleichung zu isolieren. Eliminieren Sie nach Möglichkeit ähnliche Terme, um die Gleichung zu vereinfachen.


 .
.
6. Verwenden Sie bei Bedarf zusätzliche Eigenschaften von Logarithmen. Um die Variable von anderen Termen innerhalb desselben Logarithmus zu isolieren, schreiben Sie den Term mit anderen logarithmischen Eigenschaften um.
 .
.Rund um die n Verwenden Sie zum Isolieren die Produktregel der Logarithmen:





7. Vereinfachen Sie weiter, bis Sie die Lösung gefunden haben. Wiederholen Sie die gleichen algebraischen und logarithmischen Techniken, um das Problem zu lösen. Wenn es keine ganzzahlige Lösung gibt, verwenden Sie einen Taschenrechner und auf die nächste signifikante Zahl runden.


Seit 3 = 19683, n = 19683
"Logarithmen teilen"
Оцените, пожалуйста статью