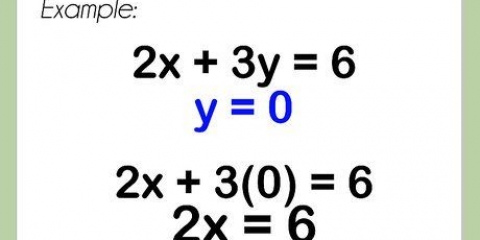Beispiel: Wir wissen das  und
und  , und somit
, und somit  .
. 
Beispiel:
Telefon  auf jeder Seite:
auf jeder Seite: 
Subtrahiere 3 von jeder Seite: 
Teilen Sie jede Seite durch 3:  .
.
Beispiel: und
und 



Beispiel: und
und 



Dies ist die gleiche Antwort wie zuvor erhalten. Wir haben keine Fehler gemacht. 
Beispiel: und
und 
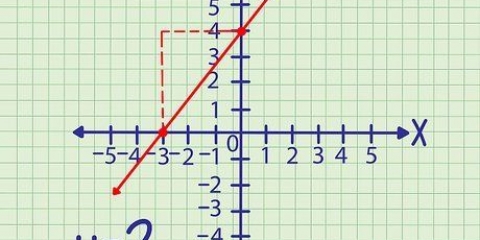
Die beiden Geraden schneiden sich im Punkt (3.6). 
Wenn die beiden Geraden parallel sind, schneiden sie sich nicht . Die x-Terme können eliminiert werden und Ihre Gleichung kann zu einer ungültigen Gleichung vereinfacht werden (z. B  ). Hinweis hier`die Linien schneiden sich nicht oder keine gültige Lösung` wenn du antwortest.
). Hinweis hier`die Linien schneiden sich nicht oder keine gültige Lösung` wenn du antwortest. Wenn die beiden Gleichungen dieselbe Gerade beschreiben, dann `schneiden` sie sich überall. Sie können die x-Terme eliminieren und Ihre Gleichung zu einer gültigen Gleichung vereinfachen (z. B  ). aufschreiben `die beiden Zeilen sind gleich` als antwort.
). aufschreiben `die beiden Zeilen sind gleich` als antwort. 

Beispiel: Finde den Schnittpunkt von  und
und  .
. Schreiben Sie die quadratische Gleichung in Bezug auf y um:  und
und  .
.Dieses Beispiel hat eine quadratische Gleichung und eine lineare Gleichung. Probleme mit zwei quadratischen Gleichungen werden auf die gleiche Weise gelöst. 
Beispiel: und
und 


Beispiel:
Subtrahiere x von jeder Seite: 
Subtrahiere 7 von jeder Seite: 

Beispiel:
Der Zweck der Faktorisierung besteht darin, die beiden Faktoren zu bestimmen, die miteinander multipliziert werden, um diese Gleichung zu erstellen. Ab dem ersten Semester wissen wir das  kann in x geteilt werden, und x. Schreiben Sie (x )(x ) = 0, um dies zu zeigen.
kann in x geteilt werden, und x. Schreiben Sie (x )(x ) = 0, um dies zu zeigen. Der letzte Term ist -6. Schreiben Sie jedes Paar von Faktoren auf, das sich multipliziert hat, um -6 als Produkt zu ergeben:  ,
,  ,
,  , und
, und  .
. Der mittlere Term ist x (was Sie als 1x schreiben können). Addiere jedes Paar von Faktoren zusammen, um 1 als Antwort zu erhalten. Das richtige Paar von Faktoren ist  , weil
, weil  .
. Füllen Sie die Lücken in Ihrer Antwort mit diesen wenigen Faktoren aus:  .
. 
Beispiel (Faktor): Am Ende haben wir die Gleichung  . Wenn beide Faktoren in Klammern gleich 0 sind, dann ist die Gleichung wahr. Die eine Lösung ist
. Wenn beide Faktoren in Klammern gleich 0 sind, dann ist die Gleichung wahr. Die eine Lösung ist  →
→  . Die andere Lösung ist
. Die andere Lösung ist  →
→  .
. Beispiel (quadratische Gleichung oder geteiltes Quadrat): Wenn Sie eine dieser Methoden verwenden, um die Gleichung zu lösen, wird eine Quadratwurzel angezeigt. Zum Beispiel wird unsere Gleichung  . Denken Sie daran, dass Sie eine Quadratwurzel auf zwei verschiedene Lösungen vereinfachen können:
. Denken Sie daran, dass Sie eine Quadratwurzel auf zwei verschiedene Lösungen vereinfachen können:  , und
, und . Schreiben Sie zwei Gleichungen, eine für jede Möglichkeit, und lösen Sie für jede von ihnen nach x auf.
. Schreiben Sie zwei Gleichungen, eine für jede Möglichkeit, und lösen Sie für jede von ihnen nach x auf. 
Eine Lösung: Die Probleme lassen sich in zwei identische Faktoren aufteilen ((x-1)(x-1) = 0). Eingegeben in die quadratische Formel wird die Quadratwurzel  . Du musst nur eine Gleichung lösen.
. Du musst nur eine Gleichung lösen. Es gibt keine wirkliche Lösung: Es gibt keine Faktoren, die die Anforderungen erfüllen (Auflistung zur Mittelfrist). Eingegeben in die quadratische Formel erhält man eine negative Zahl unter dem Radikal (wie  ). Schreibe `keine Lösung` als Antwort.
). Schreibe `keine Lösung` als Antwort. 
Beispiel: Wir haben zwei Lösungen gefunden,  und
und  . Eine unserer Linien hat die Gleichung
. Eine unserer Linien hat die Gleichung  . Ersatz
. Ersatz  und
und  , und löse jede Gleichung so, dass du erhältst
, und löse jede Gleichung so, dass du erhältst  und
und  wenn du eine antwort bekommst.
wenn du eine antwort bekommst. 
Beispiel: Wenn wir  Eingabe, wir bekommen
Eingabe, wir bekommen  , so dass ein Schnittpunkt gleich ist (2, 9). Dasselbe machen wir für die zweite Lösung und erhalten den Schnittpunkt (-3, 4) an.
, so dass ein Schnittpunkt gleich ist (2, 9). Dasselbe machen wir für die zweite Lösung und erhalten den Schnittpunkt (-3, 4) an.
Berechnen sie den schnittpunkt zweier geraden
Wenn sich gerade Linien in einem zweidimensionalen Graphen schneiden, geschieht dies nur an einem Punkt, angegeben durch die Koordinaten x und y. Da beide Geraden durch diesen Punkt verlaufen, wissen Sie, dass die x- und y-Koordinaten beide Gleichungen erfüllen müssen. Mit ein paar zusätzlichen Techniken können Sie die Schnittpunkte von Parabeln und anderen quadratischen Kurven mit derselben Logik finden.
Schritte
Methode 1 von 2: Bestimmung des Schnittpunkts zwischen zwei Geraden

1. Schreiben Sie die Gleichung einer beliebigen Geraden mit y auf der linken Seite. Ändern Sie gegebenenfalls die Gleichung so, dass y auf einer Seite des Gleichheitszeichens isoliert ist. Wenn die Gleichung mit f(x) oder g(x) anstelle von y geschrieben wird, trennen Sie diesen Term. Denken Sie daran, dass Sie Begriffe eliminieren können, indem Sie auf beiden Seiten dieselbe Operation ausführen.
- Sind die Gleichungen unbekannt?, dann bestimme es basierend auf den gegebenen Informationen.
- Beispiel: Angenommen, Sie haben zwei Zeilen
und
. Um y in der zweiten Gleichung zu trennen, addiere 12 zu jeder Seite:

2. Stellen Sie sicher, dass die rechten Seiten der Gleichungen gleich sind. Wir suchen einen Punkt, an dem die beiden Linien die gleichen x- und y-Werte haben; Dies ist der Punkt, an dem sich die Linien schneiden. Beide Gleichungen haben nur ein y auf der linken Seite, also wissen wir, dass die rechten Seiten gleich sind. Schreiben Sie eine neue Gleichung, die dies zeigt.
 und
und  , und somit
, und somit  .
.
3. Löse x in der Gleichung. Die neue Gleichung hat nur eine Variable, x. Lösen Sie dies mit Algebra, indem Sie dieselbe Operation auf beiden Seiten ausführen. Finden Sie die x-Terme jeder Seite der Gleichung und setzen Sie sie in die Form x = __ (falls nicht möglich, lesen Sie am Ende dieses Abschnitts weiter).

 auf jeder Seite:
auf jeder Seite:

 .
.
4. Verwenden Sie diesen x-Wert, um nach y . aufzulösen. Wähle die Gleichung jeder Linie. Ersetze jedes x in der Gleichung durch die gefundene Antwort. Jetzt löse nach y.
 und
und 



5. Überprüfe deine Arbeit. Es ist ratsam, Ihren x-Wert in die andere Gleichung einzufügen, um zu sehen, ob Sie das gleiche Ergebnis erhalten. Wenn Sie eine andere Lösung für y erhalten, gehen Sie zurück und überprüfen Sie Ihre Arbeit auf Fehler.
 und
und 




6. Notieren Sie die x- und y-Koordinaten des Schnittpunkts. Sie haben nun nach dem x-Wert und y-Wert des Schnittpunkts der beiden Geraden aufgelöst. Schreibe den Punkt als Koordinate mit dem x-Wert als erster Zahl.
 und
und 

7. Ungewöhnliche Ergebnisse verarbeiten. Einige Gleichungen machen es unmöglich, x . zu lösen. Das bedeutet nicht unbedingt, dass du einen Fehler gemacht hast. Es gibt zwei Möglichkeiten, wie ein Leitungspaar zu einer Sonderlösung führen kann:
 ). Hinweis hier`die Linien schneiden sich nicht oder keine gültige Lösung` wenn du antwortest.
). Hinweis hier`die Linien schneiden sich nicht oder keine gültige Lösung` wenn du antwortest. ). aufschreiben `die beiden Zeilen sind gleich` als antwort.
). aufschreiben `die beiden Zeilen sind gleich` als antwort.Methode 2 von 2: Probleme mit quadratischen Gleichungen

1. Lernen Sie quadratische Gleichungen zu erkennen. In einer quadratischen Gleichung gibt es eine oder mehrere Variablen in quadratischer Form ( oder
oder  ), und es gibt keine höheren Mächte. Die durch Gleichungen dargestellten Geraden sind gekrümmt und können daher eine Gerade in 0, 1 oder 2 Punkten schneiden. In diesem Teil erfahren Sie, wie Sie die Schnittpunkte eines solchen Problems finden.
), und es gibt keine höheren Mächte. Die durch Gleichungen dargestellten Geraden sind gekrümmt und können daher eine Gerade in 0, 1 oder 2 Punkten schneiden. In diesem Teil erfahren Sie, wie Sie die Schnittpunkte eines solchen Problems finden.
 oder
oder  ), und es gibt keine höheren Mächte. Die durch Gleichungen dargestellten Geraden sind gekrümmt und können daher eine Gerade in 0, 1 oder 2 Punkten schneiden. In diesem Teil erfahren Sie, wie Sie die Schnittpunkte eines solchen Problems finden.
), und es gibt keine höheren Mächte. Die durch Gleichungen dargestellten Geraden sind gekrümmt und können daher eine Gerade in 0, 1 oder 2 Punkten schneiden. In diesem Teil erfahren Sie, wie Sie die Schnittpunkte eines solchen Problems finden. - Berechnen Sie Gleichungen in Klammern, um zu sehen, ob sie quadratisch sind. Zum Beispiel,
ist quadratisch, weil Sie es außerhalb von Klammern setzen können, wenn
- Gleichungen eines Kreises oder einer Ellipse haben beide ein
wie ein
Begriff. Wenn Ihnen diese Sonderfälle schwer fallen, lesen Sie unter Tipps am Ende dieses Artikels weiter.

2. Schreiben Sie die Gleichungen in Bezug auf y. Schreiben Sie bei Bedarf jede Gleichung so um, dass y auf einer Seite liegt.
 und
und  .
. und
und  .
.
3. Kombinieren Sie die beiden Gleichungen, um das y . zu eliminieren. Wenn Sie beide Gleichungen gleich y gemacht haben, wissen Sie, dass die beiden Gleichungen ohne das y gleich sind.
 und
und 


4. Ordne die neue Gleichung so um, dass eine Seite gleich Null ist. Verwenden Sie mathematische Standardmethoden, um alle Terme auf einer Seite der Gleichung zu erhalten. Dies ist die erforderliche Einrichtung der Probleme, um sie im nächsten Schritt lösen zu können.




5.Löse die quadratische Gleichung. Wenn eine Seite gleich Null ist, gibt es drei Möglichkeiten, die quadratische Gleichung zu lösen. Jeder bevorzugt eine andere Methode. Sie können mehr über die quadratische Formel von lesen `das Quadrat teilen`, oder Sie können diesem Beispiel dafür weiter folgen faktorisieren Methode:

 kann in x geteilt werden, und x. Schreiben Sie (x )(x ) = 0, um dies zu zeigen.
kann in x geteilt werden, und x. Schreiben Sie (x )(x ) = 0, um dies zu zeigen. ,
,  ,
,  , und
, und  .
. , weil
, weil  .
. .
.
6. Halten Sie die Augen offen nach zwei Lösungen für x. Wenn Sie zu schnell arbeiten, finden Sie möglicherweise eine Antwort auf das Problem, ohne zu wissen, dass es eine andere gibt. So finden Sie die beiden x-Werte für Linien, die sich an zwei Punkten schneiden:
 . Wenn beide Faktoren in Klammern gleich 0 sind, dann ist die Gleichung wahr. Die eine Lösung ist
. Wenn beide Faktoren in Klammern gleich 0 sind, dann ist die Gleichung wahr. Die eine Lösung ist  →
→  . Die andere Lösung ist
. Die andere Lösung ist  →
→  .
. . Denken Sie daran, dass Sie eine Quadratwurzel auf zwei verschiedene Lösungen vereinfachen können:
. Denken Sie daran, dass Sie eine Quadratwurzel auf zwei verschiedene Lösungen vereinfachen können:  , und
, und . Schreiben Sie zwei Gleichungen, eine für jede Möglichkeit, und lösen Sie für jede von ihnen nach x auf.
. Schreiben Sie zwei Gleichungen, eine für jede Möglichkeit, und lösen Sie für jede von ihnen nach x auf.
7. Probleme mit einer oder null Lösungen lösen. Zwei Linien, die sich kaum berühren, haben einen Schnittpunkt, und zwei Linien, die sich nie berühren, haben Null. Sie können sie auf folgende Weise erkennen:
 . Du musst nur eine Gleichung lösen.
. Du musst nur eine Gleichung lösen. ). Schreibe `keine Lösung` als Antwort.
). Schreibe `keine Lösung` als Antwort.
8. Setze die x-Werte wieder in die ursprüngliche Gleichung ein. Sobald Sie den x-Wert des Schnittpunkts haben, setzen Sie ihn wieder in eine der Gleichungen ein, mit denen Sie begonnen haben. Löse nach y auf, um den y-Wert zu finden. Wenn es einen zweiten x-Wert gibt, wiederholen Sie dies auch für diesen Wert.
 und
und  . Eine unserer Linien hat die Gleichung
. Eine unserer Linien hat die Gleichung  . Ersatz
. Ersatz  und
und  , und löse jede Gleichung so, dass du erhältst
, und löse jede Gleichung so, dass du erhältst  und
und  wenn du eine antwort bekommst.
wenn du eine antwort bekommst.
9. Schreiben Sie die Antwort als Koordinaten. Jetzt schreibst du die Antwort als Koordinaten mit dem x-Wert und y-Wert des Schnittpunkts. Wenn Sie zwei Antworten haben, stellen Sie sicher, dass Sie den richtigen x-Wert mit jedem y-Wert übereinstimmen.
 Eingabe, wir bekommen
Eingabe, wir bekommen  , so dass ein Schnittpunkt gleich ist (2, 9). Dasselbe machen wir für die zweite Lösung und erhalten den Schnittpunkt (-3, 4) an.
, so dass ein Schnittpunkt gleich ist (2, 9). Dasselbe machen wir für die zweite Lösung und erhalten den Schnittpunkt (-3, 4) an.Tipps
- Gleichungen für einen Kreis oder eine Ellipse haben a
Begriff und ein
Begriff. Um den Schnittpunkt eines Kreises und einer Geraden zu finden, lösen Sie nach x innerhalb der linearen Gleichung. Setzen Sie die Lösung für x in die Kreisgleichung ein, und die quadratische Gleichung ist jetzt viel einfacher. Diese Probleme können 0, 1 oder 2 Lösungen haben, wie bereits in den obigen Methoden angegeben.
- Ein Kreis und eine Parabel (oder jede andere quadratische Gleichung) können 0, 1, 2, 3 oder 4 Lösungen haben. Finden Sie die Variable, die in beiden Gleichungen ein Quadrat ist – sagen wir, dies ist x. lose
an und ersetzen Sie die Antwort für
in der anderen Gleichung. Löse y auf, um die 0, 1 oder 2 Lösungen zu finden. Setze jede Lösung wieder in die ursprüngliche quadratische Gleichung ein und löse nach x. Jede davon kann 0, 1 oder 2 Lösungen haben.
"Berechnen sie den schnittpunkt zweier geraden"
Оцените, пожалуйста статью