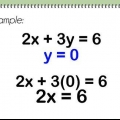Es ist ein Punkt und eine Steigung gegeben. Es werden zwei Punkte vergeben, aber keine Steigung. Gegeben einen Punkt und eine weitere Linie parallel dazu. Gegeben sei ein Punkt und eine weitere Gerade senkrecht dazu. 




Ordne deine Gleichung um. b = y - mx. Werte eingeben und lösen. b = -5 - (2/3)6. b = -5 - 4. b = -9 Überprüfen Sie, ob der Schnittpunkt mit der y-Achse wirklich -9 . beträgt. Schreiben Sie die Gleichung auf: y = 2/3 x - 9 

Verwenden Sie Ihre Steigung und Koordinaten in der obigen Gleichung. Multiplizieren Sie die Steigung (m) mit der x-Koordinate des Punktes. Subtrahiere den Wert von der y-Koordinate des Punktes. du hast jetzt B gelöst, der Schnittpunkt mit der y-Achse. 



Berechnen Sie die Steigung. Die Steigung = (Y2 - Ja1) / (X2 - x1) -12 - (-5) / 8 - 6 = -7 / 2 Die Steigung ist -7/2 (vom ersten Punkt zum zweiten gehen wir 7 nach unten und 2 nach rechts, also ist die Steigung -7 über 2). Ordne deine Gleichung um. b = y - mx. Werte eingeben und lösen. b = -12 - (-7/2)8. b = -12 - (-28). b = -12 + 28. b = 16 Anmerkung: da wir die 8 für die Koordinaten verwendet haben, müssen wir auch die -12 . verwenden.Wenn Sie die 6 für Ihre Koordinaten verwenden, müssen Sie auch die -5 . verwenden. Überprüfen Sie, ob Ihr Schnittpunkt mit der y-Achse wirklich 16 . beträgt. Schreiben Sie die Gleichung auf: y = -7/2 x + 16 
Ersetzen Sie die Steigung und die Koordinaten in der obigen Gleichung. Multiplizieren Sie die Steigung (m) mit der x-Koordinate des Punktes. Subtrahiere den Wert von der y-Koordinate des Punktes. Du hast B gelöst, der Schnittpunkt mit der y-Achse. 


Löse die Steigung. Die Steigung unserer neuen Linie entspricht der Steigung der alten Linie. Bestimmen Sie die Steigung der alten Linie: -2y = -5x + 1 ziehen "-2" von beiden Seiten ab: y = 5/2x - 1/2 Die Steigung ist 5/2. Ordne deine Gleichung um. b = y - mx. Ausfüllen und lösen. b = 3 - (5/2)4. b = 3 - (10). b = -7. Überprüfen Sie, ob der Schnittpunkt mit der y-Achse wirklich -7 . beträgt. Schreiben Sie die Gleichung auf: y = 5/2 x - 7 
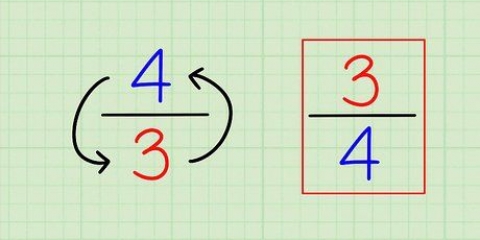
2/3 wird -3/2 -Aus 6/5 wird 5/6 3 (oder 3/1 — ist gleich) wird -1/3 -1/2 wird 2 
Setze deine Steigung und deine Koordinaten in die obige Gleichung ein. Multiplizieren Sie die Steigung (m) mit der x-Koordinate des Punktes. Subtrahiere diesen Wert von der y-Koordinate des Punktes. Sie haben nun die Gleichung gelöst nach B; der Schnittpunkt mit der y-Achse. 


Löse die Steigung. Die Steigung unserer neuen Geraden wird zum negativen Kehrwert der Steigung der alten Geraden. Bestimmen Sie die Steigung der alten Linie: 2y = -4x + 9 ziehen "2" von beiden Seiten: y = -4/2x + 9/2 Die Steigung ist -4/2 oder -2. Der negative Kehrwert von -2 ist 1/2. ordne deine Gleichung um. b = y - mx. Ausfüllen und lösen. b = -1 - (1/2)8. b = -1 - (4). b = -5. Überprüfen Sie, ob Ihr Schnittpunkt mit der y-Achse wirklich -5 . beträgt. Schreiben Sie die Gleichung: y = 1/2 x - 5
Finden der geradengleichung
Um die Gleichung einer Geraden zu finden, haben Sie brauche zwei dinge:a) ein Punkt auf der Linie; und b) die Steigung (manchmal auch die Steigung) der Geraden. Aber wie man diese beiden Informationen sammelt und was man danach damit macht, kann je nach Situation sehr unterschiedlich sein. Der Einfachheit halber konzentriert sich dieser Artikel auf Gleichungen der Form y = mx + b anstatt (y - y1) = m(x - x1).
Schritte
Methode 1 von 5: Allgemeine Informationen
1. Wissen, wonach Sie suchen müssen.Bevor Sie nach dem Vergleich suchen können, müssen Sie genau wissen, was Sie finden möchten. Beachten Sie Folgendes:
- Punkte werden klassifiziert als geordnetes Paar, wie (-7, -8) oder (-2,-6).
- Die erste Zahl in einem geordneten Paar ist die x-Koordinate. Dies ist die horizontale Position des Punktes (wie viele Einheiten links oder rechts vom Ursprung).
- Die zweite Zahl in einem geordneten Paar ist die y-Koordinate. Dies ist die vertikale Position des Punktes (wie viele Einheiten nach oben oder unten vom Ursprung).
- Der Neigung zwischen den beiden Punkten heißt der "die Piste" — mit anderen Worten, wie weit Sie nach oben (oder unten) und rechts (oder links) gehen müssen, um von einem Punkt zum anderen zu gelangen.
- Zwei Zeilen sind parallel wenn sie sich nicht schneiden.
- Zwei Linien stehen senkrecht aufeinander wenn sie sich im rechten Winkel (90 Grad) schneiden.
2. Bestimmen Sie, mit welcher Art von Auftrag Sie es zu tun haben.
3. Gehen Sie das Problem mit einer der folgenden vier Methoden an. Abhängig von den gegebenen Informationen gibt es verschiedene Möglichkeiten, es zu lösen.
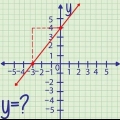
Methode 2 von 5: Ein Punkt und eine Steigung sind gegeben

1. Finden Sie den Schnittpunkt Ihrer Gleichung mit der y-Achse. Der Schnittpunkt mit der y-Achse (oder die Variable B in unserer Gleichung) ist der Schnittpunkt der Geraden mit der y-Achse. Sie können den Schnittpunkt mit der y-Achse berechnen, indem Sie die Gleichung neu anordnen, um nach aufzulösen B. Unsere neue Gleichung sieht nun so aus: b = y - mx.
- Geben Sie Ihre Steigung und Koordinaten in die obige Gleichung ein.
- Multiplizieren Sie die Steigung (m) mit der x-Koordinate des Punktes.
- Subtrahiere diesen Wert von der y-Koordinate des Punktes.
- Jetzt hast du B gelöst, der Schnittpunkt mit der y-Achse.

2. Schreiben Sie die Formel auf:y = ____ x + ____ , zusammen mit den Leerzeichen.

3. Füllen Sie den ersten leeren Raum, den für das x, mit der Steigung aus.

4. Füllen Sie die zweite Lücke mit dem Schnittpunkt mit der y-Achse das hast du vorher berechnet.

5. Lösen Sie das Beispielproblem. "Gegeben den Punkt (6, -5) und die Steigung 2/3, wie lautet die Geradengleichung?"
Methode 3 von 5: Es werden zwei Punkte vergeben
1. Berechnen Sie die Steigung zwischen zwei Punkten. Die Steigung wird auch als bezeichnet Neigung und Sie können sich dies als die Geschwindigkeit vorstellen, mit der sich etwas entlang einer imaginären y- und x-Achse bewegt. Die Gleichung für die Steigung lautet: (Y2 - Ja1) / (X2 - x1)
- Nimm die beiden Punkte und verwende sie in der Gleichung (zwei Koordinaten bedeuten zwei ja-Werte und zwei x-Werte). Es spielt keine Rolle, welche Koordinaten Sie zuerst eingeben, solange Sie dies konsequent tun. Einige Beispiele:
- Punkte (3, 8) und (7, 12). (Y2 - Ja1) / (X2 - x1) = 12 - 8 / 7 - 3 = 4/4 oder 1.
- Punkte (5, 5) und (9, 2). (Y2 - Ja1) / (X2 - x1) = 2 - 5 / 9 - 5 = -3/4.

2. Wählen Sie einen Satz von Koordinaten für den Rest des Problems. Streichen Sie die anderen Koordinaten durch oder decken Sie sie ab, damit Sie sie nicht versehentlich verwenden.

3. Berechnen Sie den Schnittpunkt mit der y-Achse Ihrer Gleichung. Ordne wieder die Formel y = mx + b um, um eine Gleichung der Form b = y – mx . zu erhalten. Es ist immer noch dieselbe Gleichung; du hast es gerade neu geordnet.

4. Schreiben Sie die Formel auf:y = ____ x + ____ , einschließlich der Leerzeichen.

5. Füllen Sie den ersten leeren Raum, den für das x, mit der Steigung aus.

6. Füllen Sie die zweite Lücke mit dem Schnittpunkt mit der y-Achse.

7. Lösen Sie das Beispielproblem. "Gegeben die Punkte (6, -5) und (8, -12), wie lautet die Geradengleichung?"
Methode 4 von 5: Wenn ein Punkt und eine parallele Linie gegeben sind
1. Bestimmen Sie die Steigung der parallelen Linie. Denken Sie daran, dass die Steigung der Koeffizient von ist x wodurch ja hat keinen Koeffizienten.
- In einer Gleichung wie y = 3/4 x + 7 beträgt die Steigung 3/4.
- In einer Gleichung wie y = 3x - 2 beträgt die Steigung 3.
- In einer Gleichung wie y = 3x beträgt die Steigung immer noch 3.
- In einer Gleichung wie y = 7 ist die Steigung null (weil das Problem null x enthält).
- In einer Gleichung wie y = x - 7 beträgt die Steigung 1.
- In einer Gleichung wie -3x + 4y = 8 beträgt die Steigung 3/4.
- Um die Steigung einer solchen Gleichung zu finden, ordnen Sie sie einfach so um, dass ja ist isoliert:
- 4y = 3x + 8
- Teilen Sie beide Seiten durch 4: y = 3/4x + 2

2. Berechnen Sie den Schnittpunkt mit der y-Achse, indem Sie die Steigung aus dem ersten Schritt und die Gleichung b = y - mx . verwenden.

3. Schreiben Sie die Formel auf:y = ____ x + ____ , mit den Leerzeichen.

4. Füllen Sie das erste leere Feld vor dem x mit der Steigung aus, die Sie in Schritt 1 ermittelt haben.Das Bemerkenswerte an parallelen Linien ist, dass sie die gleiche Steigung haben, sodass du am Ende das bekommst, womit du angefangen hast.

5. Füllen Sie den Schnittpunkt mit der y-Achse in das zweite leere Feld.
6. Lösen Sie das Beispielproblem. "Gegeben der Punkt (4, 3) und die parallele Linie 5x - 2y = 1; Wie lautet die Geradengleichung??"
Methode 5 von 5: Mit einem gegebenen Punkt und einer senkrechten Linie
1. Finden Sie die Steigung der gegebenen Linie. Weitere Informationen finden Sie in den obigen Beispielen.

2. Finden Sie den negativen Kehrwert dieser Steigung. Mit anderen Worten, drehen Sie es um und ändern Sie das Vorzeichen. Der Punkt mit senkrechten Linien ist, dass sie eine negative inverse Steigung haben, daher müssen Sie die Steigung ändern, bevor Sie sie verwenden können.

3. Berechnen Sie den Schnittpunkt mit der y-Achse mit der Steigung ab Schritt 2 und die Gleichung b = y - mx

4. Schreiben Sie die Formel auf:y = ____ x + ____ , mit den Leerzeichen.

5. Füllen Sie das erste leere Feld vor dem x mit der Steigung aus, die Sie in Schritt 2 berechnet haben.

6. Füllen Sie den Schnittpunkt mit der y-Achse in das zweite leere Feld.
7. Lösen Sie das Beispielproblem. "Gegeben (8, -1) und und die Senkrechte 4x + 2y = 9; Wie lautet die Geradengleichung??"
Оцените, пожалуйста статью