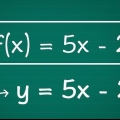Beispiel: Der Kehrwert von 2 ist 1 ÷ 2 = /2. 

2/5 = 1 + 1 + /5 = /5 + /5 + /5 = /5 = /5. 
Im obigen Beispiel /5 die Umkehrung von /14. 

Der Kehrwert von 0,4 ist beispielsweise 1 ÷ 0,4. 
Sie können zum Beispiel 1 0.4 nehmen und als 10 ÷ 4 . umschreiben. In diesem Fall haben Sie jede Dezimalstelle um eine Stelle nach rechts verschoben, was der Multiplikation jeder Zahl mit zehn entspricht. 
Den kehrwert einer zahl finden
Der Kehrwert einer Zahl ist in allen möglichen algebraischen Gleichungen nützlich. Wenn Sie beispielsweise einen Bruch durch einen anderen dividieren, multiplizieren Sie im Grunde den ersten Bruch mit dem Kehrwert des zweiten. Möglicherweise benötigen Sie diese Reziprozität auch, wenn Sie eine Geradengleichung finden.
Schritte
Methode 1 von 3: Den Kehrwert eines Bruchs oder einer ganzen Zahl ermitteln

1. Ermitteln Sie den Kehrwert eines Bruchs, indem Sie ihn umkehren. Die Definition von `das Inverse` ist einfach. Um den Kehrwert einer beliebigen Zahl zu finden, schreiben oder berechnen Sie einfach `1 ÷ (diese Zahl)`. Bei einem Bruch ist die Umkehrung nur ein weiterer Bruch, bei dem die Zahlen umgekehrt sind oder umgekehrt.
- Die Umkehrung von /4 ist deshalb /3.
- Das Produkt einer Zahl und ihres Kehrwertes ist immer gleich 1.

2. Schreibe den Kehrwert einer ganzen Zahl als Bruch. Auch hier ist der Kehrwert einer Zahl immer 1 ÷ (diese Zahl). Für eine ganze Zahl schreiben Sie das als Bruch – es macht keinen Sinn, sie auf das Komma zu berechnen.
Methode 2 von 3: Bestimmung der Umkehrung einer zusammengesetzten Zahl

1. Eine zusammengesetzte Zahl erkennen. Zusammengesetzte Zahlen sind eine Kombination aus einer ganzen Zahl und einem Bruch, z. B. 2/5.Es gibt zwei Schritte, um den Kehrwert einer gemischten Zahl zu finden, die unten erklärt werden.

2. Verwandle es in einen unechten Bruch. Denken Sie daran, dass die Zahl 1 immer als (Zahl)/(gleiche Zahl) geschrieben werden kann und dass Brüche mit demselben Nenner (der unteren Zahl) zusammenaddiert werden können. Hier ist ein Beispiel mit 2/5:

3. Den Bruch umkehren. Sobald die Zahl vollständig als Bruch geschrieben ist, können Sie den Kehrwert wie bei jedem Bruch finden, indem Sie ihn einfach umdrehen.
Methode 3 von 3: Den Kehrwert einer Dezimalzahl bestimmen

1. Konvertieren Sie eine Dezimalzahl in einen Bruch (wenn möglich). Vielleicht erkennen Sie einige gängige Dezimalzahlen, die einfach sind kann als Bruch geschrieben werden.Zum Beispiel: 0,5 = /2 und 0,25 = /4. Einmal in Form eines Bruchs, kehren Sie den Bruch um, so dass Sie mit der Umkehrung übrig bleiben.
- Der Kehrwert von 0,5 ist beispielsweise /1 = 2.

2. Schreiben Sie ein Freigabeproblem auf. Wenn du es nicht in einen Bruch umwandeln kannst, schreibe oder berechne den Kehrwert dieser Zahl als Divisionsaufgabe: 1 ÷ (die Dezimalzahl). Sie können einen Taschenrechner verwenden, um dies zu lösen, oder zum nächsten Schritt übergehen, um es von Hand zu lösen.

3. Ändere das Divisionsproblem, um ganze Zahlen zu verwenden. Der erste Schritt zu Dezimalzahlen dividieren verschiebt den Dezimalpunkt, bis alle Zahlen ganze Zahlen sind. Solange Sie das Komma für beide Zahlen um die gleiche Anzahl von Stellen verschieben, erhalten Sie die richtige Antwort.

4. Lösen Sie das Problem mit der langen Division. Verwendung eine lange Division die Umkehrung berechnen. Wenn Sie damit 10 ÷ 4 berechnen, erhalten Sie die Antwort 2.5 (der Kehrwert von 0,4).
Tipps
- Die negative Umkehrung einer Zahl ist gleich der regulären Umkehrung multipliziert mit -1. Der negative Kehrwert von /4 ist -/3.
- Eine Umkehrung wird manchmal auch als bezeichnet multiplikativ invers genannt.
- Die Zahl 1 ist ihr eigener Kehrwert, da 1 ÷ 1 = 1.
- Die Zahl 0 hat keine Umkehrung, denn 1 ÷ 0 ist undefiniert.
Оцените, пожалуйста статью