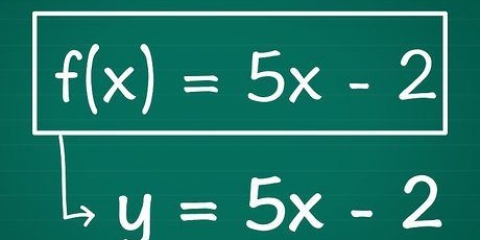Wir arbeiten weiter mit dem gleichen Beispiel,  Wähle die zweite und dritte Zahl des Sets. tun
Wähle die zweite und dritte Zahl des Sets. tun  und Sie werden sehen, dass die Differenz immer noch 3 . beträgt. Um dies zu bestätigen, wählen Sie ein anderes Beispiel und machen Sie
und Sie werden sehen, dass die Differenz immer noch 3 . beträgt. Um dies zu bestätigen, wählen Sie ein anderes Beispiel und machen Sie  um herauszufinden, dass der Unterschied konstant 3 . beträgt. Sie können jetzt einigermaßen sicher sein, dass Sie es mit einer arithmetischen Folge zu tun haben.
um herauszufinden, dass der Unterschied konstant 3 . beträgt. Sie können jetzt einigermaßen sicher sein, dass Sie es mit einer arithmetischen Folge zu tun haben. Es ist möglich, dass eine Menge von Zahlen die Eigenschaften einer arithmetischen Folge basierend auf den ersten paar Zahlen hat und dann davon abweicht. Nehmen Sie zum Beispiel das Set  ... Der Unterschied zwischen der ersten und zweiten Zahl ist 1 und der Unterschied zwischen der zweiten und dritten Zahl ist ebenfalls 1. Der Unterschied zwischen der dritten und vierten Zahl beträgt jedoch 3. Da die Differenz nicht für alle Zahlen in der ganzen Menge gilt, ist dies keine arithmetische Folge.
... Der Unterschied zwischen der ersten und zweiten Zahl ist 1 und der Unterschied zwischen der zweiten und dritten Zahl ist ebenfalls 1. Der Unterschied zwischen der dritten und vierten Zahl beträgt jedoch 3. Da die Differenz nicht für alle Zahlen in der ganzen Menge gilt, ist dies keine arithmetische Folge. 
Zum Beispiel im Beispiel von  ..., Sie können die nächste Zahl in der Menge bestimmen, indem Sie den Differenzfaktor 3 zur letzten gegebenen Zahl addieren. tun
..., Sie können die nächste Zahl in der Menge bestimmen, indem Sie den Differenzfaktor 3 zur letzten gegebenen Zahl addieren. tun  und du bekommst 16, das ist die nächste Zahl. Sie können weitere 3 hinzufügen, um die Sequenz so lang zu machen, wie Sie möchten. Die Reihenfolge kann beispielsweise sein
und du bekommst 16, das ist die nächste Zahl. Sie können weitere 3 hinzufügen, um die Sequenz so lang zu machen, wie Sie möchten. Die Reihenfolge kann beispielsweise sein ... Du kannst auf unbestimmte Zeit damit fortfahren.
... Du kannst auf unbestimmte Zeit damit fortfahren. 

In unserem Beispiel,  ,____,
,____, ..., die Unbekannte ist gleich 4 und die Differenz dieser Reihe beträgt ebenfalls 4. Das wird also addiert
..., die Unbekannte ist gleich 4 und die Differenz dieser Reihe beträgt ebenfalls 4. Das wird also addiert  und so erhalten Sie 8, die Zahl, die für das Unbekannte ausgefüllt werden kann.
und so erhalten Sie 8, die Zahl, die für das Unbekannte ausgefüllt werden kann. 
Im Beispiel,  ,___,
,___, …, die Zahl unmittelbar nach dem Unbekannten ist gleich 12. Ziehen Sie von dieser Zahl den Differenzfaktor 4 ab und Sie erhalten
…, die Zahl unmittelbar nach dem Unbekannten ist gleich 12. Ziehen Sie von dieser Zahl den Differenzfaktor 4 ab und Sie erhalten  . Das Ergebnis 8 kann dann für das Unbekannte ausgefüllt werden.
. Das Ergebnis 8 kann dann für das Unbekannte ausgefüllt werden. 
Im Beispiel sind die beiden Ergebnisse von  und
und  beide antworten 8. Die fehlende Zahl in dieser arithmetischen Folge ist also 8. Die komplette Serie ist
beide antworten 8. Die fehlende Zahl in dieser arithmetischen Folge ist also 8. Die komplette Serie ist  ...
... 


Die Zahl a(n) kann als „die n-te Zahl von a“ gelesen werden, wobei n die Zahl in der zu findenden Folge und a(n) der tatsächliche Wert dieser Zahl ist. Wenn Sie beispielsweise aufgefordert werden, das hundertste Element einer arithmetischen Folge zu finden, ist n gleich 100. Beachten Sie, dass in diesem Beispiel n gleich 100 ist, aber a(n) der Wert der hundertsten Zahl ist, nicht die Zahl 100 selbst. 
Zum Beispiel in diesem Beispiel,  … wissen wir, dass a(1), die erste Zahl, gleich 3 ist und dass der Differenzfaktor d gleich 5 . ist. Angenommen, Sie werden aufgefordert, die hundertste Zahl in dieser Folge zu finden. Dann n=100 und (n-1)=99. Die vollständige explizite Formel mit den eingegebenen Daten lautet dann
… wissen wir, dass a(1), die erste Zahl, gleich 3 ist und dass der Differenzfaktor d gleich 5 . ist. Angenommen, Sie werden aufgefordert, die hundertste Zahl in dieser Folge zu finden. Dann n=100 und (n-1)=99. Die vollständige explizite Formel mit den eingegebenen Daten lautet dann  . Dies kann auf 498 vereinfacht werden, die hundertste Zahl in dieser Reihe.
. Dies kann auf 498 vereinfacht werden, die hundertste Zahl in dieser Reihe. 

Verwenden Sie die Gleichung  und geben Sie alle Informationen ein, die Sie haben. Da Sie wissen, dass die 50. Zahl 300 ist, wissen Sie auch, dass n=50, n-1=49 und a(n)=300. Außerdem ist der Differenzfaktor d angegeben, der 7 . beträgt. Die Formel wird also
und geben Sie alle Informationen ein, die Sie haben. Da Sie wissen, dass die 50. Zahl 300 ist, wissen Sie auch, dass n=50, n-1=49 und a(n)=300. Außerdem ist der Differenzfaktor d angegeben, der 7 . beträgt. Die Formel wird also  . Das wird ausgearbeitet
. Das wird ausgearbeitet  . Die Sequenz, die Sie mit 43 begonnen haben, hat einen Differenzfaktor von 7. Die Sequenz sieht also aus wie 43,50,57,64,71,78…293,300.
. Die Sequenz, die Sie mit 43 begonnen haben, hat einen Differenzfaktor von 7. Die Sequenz sieht also aus wie 43,50,57,64,71,78…293,300. 
Angenommen, Sie wissen, dass eine bestimmte arithmetische Folge mit 100 beginnt und sich mit 13 . addiert. Darüber hinaus ist auch angegeben, dass die letzte Zahl 2856 . ist. Um die Länge der Folge zu ermitteln, verwenden Sie die Zahlen a1=100, d=13 und a(n)=2856. Wenden Sie diese Zahlen auf die Formel an, um zu erhalten  . Wenn du das herausgefunden hast, bekommst du
. Wenn du das herausgefunden hast, bekommst du  , was gleich 212+1 ist, was wiederum 213 . ist. Es gibt 213 Zahlen in dieser Folge.
, was gleich 212+1 ist, was wiederum 213 . ist. Es gibt 213 Zahlen in dieser Folge. Dieses Beispiel sieht aus wie 100, 113, 126, 139… 2843, 2856.
Bestimmen jedes glieds einer arithmetischen folge
Eine arithmetische Folge ist jede Folge von Zahlen, die sich fortlaufend um einen konstanten Wert voneinander unterscheiden. Zum Beispiel die Folge der geraden Zahlen, 
Schritte
Methode 1 von 4: Finden der nächsten Zahl in einer arithmetischen Folge

1. Finden Sie den Differenzfaktor der Reihe. Wenn Ihnen eine Zahlensammlung präsentiert wird, kann es sein, dass es sich um eine arithmetische Folge handelt, oder Sie müssen diese selbst erfinden. Zumindest der erste Schritt ist der gleiche. Wählen Sie die ersten beiden aufeinanderfolgenden Zahlen im Set aus. Subtrahiere die erste Zahl von der zweiten Zahl. Das Ergebnis ist der Differenzfaktor Ihrer Serie.
- Angenommen, Sie haben die Sammlung
.... Dann tu es
um den Differenzfaktor 3 zu erhalten.
- Angenommen, Sie haben eine Sammlung absteigender Zahlen, wie z
... Dann subtrahiert man immer noch die erste Zahl von der zweiten, um die Differenz zu finden. In diesem Fall ergibt dies
. Das negative Ergebnis bedeutet, dass Ihre Sammlung von links nach rechts abnimmt. Stellen Sie immer sicher, dass das Vorzeichen der Differenz der Richtung entspricht, in die die Zahlen zu gehen scheinen.

2. Prüfen Sie, ob der Differenzfaktor konstant ist. Die Bestimmung des Differenzfaktors nur für die ersten beiden Zahlen stellt nicht sicher, dass die Menge eine arithmetische Folge ist. Sie müssen sicher sein, dass der Unterschied während der gesamten Serie konstant gehalten wird. Überprüfen Sie den Unterschied, indem Sie zwei aufeinanderfolgende Zahlen in der Menge subtrahieren. Wenn das Ergebnis für ein oder zwei andere Zahlenpaare konsistent ist, haben Sie es wahrscheinlich mit einer arithmetischen Folge zu tun.
 Wähle die zweite und dritte Zahl des Sets. tun
Wähle die zweite und dritte Zahl des Sets. tun  und Sie werden sehen, dass die Differenz immer noch 3 . beträgt. Um dies zu bestätigen, wählen Sie ein anderes Beispiel und machen Sie
und Sie werden sehen, dass die Differenz immer noch 3 . beträgt. Um dies zu bestätigen, wählen Sie ein anderes Beispiel und machen Sie  um herauszufinden, dass der Unterschied konstant 3 . beträgt. Sie können jetzt einigermaßen sicher sein, dass Sie es mit einer arithmetischen Folge zu tun haben.
um herauszufinden, dass der Unterschied konstant 3 . beträgt. Sie können jetzt einigermaßen sicher sein, dass Sie es mit einer arithmetischen Folge zu tun haben. ... Der Unterschied zwischen der ersten und zweiten Zahl ist 1 und der Unterschied zwischen der zweiten und dritten Zahl ist ebenfalls 1. Der Unterschied zwischen der dritten und vierten Zahl beträgt jedoch 3. Da die Differenz nicht für alle Zahlen in der ganzen Menge gilt, ist dies keine arithmetische Folge.
... Der Unterschied zwischen der ersten und zweiten Zahl ist 1 und der Unterschied zwischen der zweiten und dritten Zahl ist ebenfalls 1. Der Unterschied zwischen der dritten und vierten Zahl beträgt jedoch 3. Da die Differenz nicht für alle Zahlen in der ganzen Menge gilt, ist dies keine arithmetische Folge.
3. Addiere den Differenzfaktor zur letzten Zahl. Es ist einfach, die nächste Zahl in einer arithmetischen Folge zu finden, wenn Sie den Differenzfaktor kennen. Addiere einfach den Differenzfaktor zur letzten letzten Zahl des Sets und du erhältst die folgende Zahl.
 ..., Sie können die nächste Zahl in der Menge bestimmen, indem Sie den Differenzfaktor 3 zur letzten gegebenen Zahl addieren. tun
..., Sie können die nächste Zahl in der Menge bestimmen, indem Sie den Differenzfaktor 3 zur letzten gegebenen Zahl addieren. tun  und du bekommst 16, das ist die nächste Zahl. Sie können weitere 3 hinzufügen, um die Sequenz so lang zu machen, wie Sie möchten. Die Reihenfolge kann beispielsweise sein
und du bekommst 16, das ist die nächste Zahl. Sie können weitere 3 hinzufügen, um die Sequenz so lang zu machen, wie Sie möchten. Die Reihenfolge kann beispielsweise sein ... Du kannst auf unbestimmte Zeit damit fortfahren.
... Du kannst auf unbestimmte Zeit damit fortfahren.Methode 2 von 4: Suchen Sie nach einer fehlenden Zahl

1. Bestätigen Sie, dass Sie mit einer arithmetischen Folge beginnen. In einigen Fällen haben Sie es mit einer Sammlung von Zahlen zu tun, bei denen eine Zahl in der Mitte fehlt. Wie bereits erwähnt, überprüfen Sie zunächst, ob Ihre Sammlung eine arithmetische Folge ist. Wählen Sie zwei aufeinanderfolgende Zahlen aus und finden Sie den Unterschied zwischen ihnen. Dann vergleiche dies mit zwei anderen aufeinanderfolgenden Zahlen in der Folge. Wenn der Unterschied gleich ist, können Sie davon ausgehen, dass es sich um eine arithmetische Folge handelt, und Sie können fortfahren.
- Angenommen, Sie haben die Sequenz
,___,
... Beginnen Sie mit dem Abzug
und du bekommst 4 als Differenz. Vergleichen Sie dies mit zwei anderen aufeinanderfolgenden Zahlen, wie z
. Der Unterschied beträgt wieder 4. Sie können jetzt fortfahren.

2. Addiere den Differenzfaktor zur Zahl für den leeren Raum. Dies entspricht dem Hinzufügen einer Zahl am Ende einer Sequenz. Finden Sie die Zahl unmittelbar vor dem leeren Platz in Ihrer Sequenz. Dies ist die `letzte` bekannte Nummer. Addiere die gefundene Differenz zu dieser Zahl, und du erhältst die Zahl, die an die Stelle des Unbekannten passen sollte.
 ,____,
,____, ..., die Unbekannte ist gleich 4 und die Differenz dieser Reihe beträgt ebenfalls 4. Das wird also addiert
..., die Unbekannte ist gleich 4 und die Differenz dieser Reihe beträgt ebenfalls 4. Das wird also addiert  und so erhalten Sie 8, die Zahl, die für das Unbekannte ausgefüllt werden kann.
und so erhalten Sie 8, die Zahl, die für das Unbekannte ausgefüllt werden kann.
3. Subtrahiere den Differenzfaktor von der Zahl nach dem Unbekannten. Um sicherzustellen, dass Sie die richtige Antwort gefunden haben, überprüfen Sie noch einmal aus der anderen Richtung. Eine arithmetische Folge sollte konsequent in eine bestimmte Richtung gehen. Wenn Sie von links nach rechts gehen und 4 hinzufügen, können Sie von rechts nach links das Gegenteil tun und 4 von der vorherigen Zahl subtrahieren.
 ,___,
,___, …, die Zahl unmittelbar nach dem Unbekannten ist gleich 12. Ziehen Sie von dieser Zahl den Differenzfaktor 4 ab und Sie erhalten
…, die Zahl unmittelbar nach dem Unbekannten ist gleich 12. Ziehen Sie von dieser Zahl den Differenzfaktor 4 ab und Sie erhalten  . Das Ergebnis 8 kann dann für das Unbekannte ausgefüllt werden.
. Das Ergebnis 8 kann dann für das Unbekannte ausgefüllt werden.
4. Vergleichen Sie Ihre Ergebnisse. Die beiden Ergebnisse, die Sie durch Addieren (von links nach rechts) oder Subtrahieren (von rechts nach links) erhalten, sollten übereinstimmen. Wenn ja, dann haben Sie die fehlende Nummer gefunden. Wenn sie nicht übereinstimmen, müssen Sie Ihre Arbeit erneut überprüfen. Vielleicht haben Sie es nicht mit einer reinen arithmetischen Folge zu tun.
 und
und  beide antworten 8. Die fehlende Zahl in dieser arithmetischen Folge ist also 8. Die komplette Serie ist
beide antworten 8. Die fehlende Zahl in dieser arithmetischen Folge ist also 8. Die komplette Serie ist  ...
...Methode 3 von 4: Bestimme einen beliebigen Term einer arithmetischen Folge

1. Finde die erste Zahl der Reihe. Nicht jede Sequenz beginnt mit den Zahlen 0 oder 1. Schauen Sie sich die Zahlen an, die Sie haben, und finden Sie die erste Zahl. Dies ist Ihr Ausgangspunkt, der mit Variablen wie a(1) identifiziert werden kann.
- Bei arithmetischen Folgen ist es üblich, mit der Variablen a(1) zu arbeiten, die die erste Zahl der Folge darstellt. Sie können natürlich jede Variable wählen, aber das Ergebnis sollte das gleiche sein.
- Zum Beispiel angesichts der Reihe
…, ist die erste Zahl
, was mathematisch als a(1) bezeichnet werden kann.

2. Bestimmen Sie den Differenzfaktor als d. Bestimmen Sie den Differenzfaktor für die Reihe wie oben angegeben. In diesem Beispiel ist der Differenzfaktor gleich  , und daher 5. Beim Vergleich mit den anderen Zahlen in der Folge erhält man das gleiche Ergebnis. Diesen Differenzfaktor bezeichnen wir mit der mathematischen Variablen d.
, und daher 5. Beim Vergleich mit den anderen Zahlen in der Folge erhält man das gleiche Ergebnis. Diesen Differenzfaktor bezeichnen wir mit der mathematischen Variablen d.
 , und daher 5. Beim Vergleich mit den anderen Zahlen in der Folge erhält man das gleiche Ergebnis. Diesen Differenzfaktor bezeichnen wir mit der mathematischen Variablen d.
, und daher 5. Beim Vergleich mit den anderen Zahlen in der Folge erhält man das gleiche Ergebnis. Diesen Differenzfaktor bezeichnen wir mit der mathematischen Variablen d.
3. Verwenden Sie die explizite Formel. Eine explizite Formel ist eine mathematische Gleichung, mit der Sie eine beliebige Zahl in einer arithmetischen Folge finden können, ohne die gesamte Folge ausschreiben zu müssen. Die explizite Formel für eine mathematische Folge ist  .
.
 .
.
4. Geben Sie alle Details ein, um das Problem zu lösen. Verwenden Sie diese explizite Formel für Ihre Sequenz, und geben Sie alle Ihnen zur Verfügung stehenden Daten ein, um die benötigte Zahl zu bestimmen.
 … wissen wir, dass a(1), die erste Zahl, gleich 3 ist und dass der Differenzfaktor d gleich 5 . ist. Angenommen, Sie werden aufgefordert, die hundertste Zahl in dieser Folge zu finden. Dann n=100 und (n-1)=99. Die vollständige explizite Formel mit den eingegebenen Daten lautet dann
… wissen wir, dass a(1), die erste Zahl, gleich 3 ist und dass der Differenzfaktor d gleich 5 . ist. Angenommen, Sie werden aufgefordert, die hundertste Zahl in dieser Folge zu finden. Dann n=100 und (n-1)=99. Die vollständige explizite Formel mit den eingegebenen Daten lautet dann  . Dies kann auf 498 vereinfacht werden, die hundertste Zahl in dieser Reihe.
. Dies kann auf 498 vereinfacht werden, die hundertste Zahl in dieser Reihe.Methode 4 von 4: Verwenden Sie die explizite Formel, um mehr Daten zu erhalten

1. Ordne die explizite Formel um, um andere Variablen zu finden. Verwenden Sie die explizite Formel und einige einfache Algebra, um verschiedene Informationen über die arithmetische Folge zu finden. In seiner ursprünglichen Form ( ), ist die explizite Formel zum Lösen von an und gibt dir die n-te Zahl der Reihe. Sie können diese Formel jedoch mathematisch manipulieren, um auch nach anderen Variablen aufzulösen.
), ist die explizite Formel zum Lösen von an und gibt dir die n-te Zahl der Reihe. Sie können diese Formel jedoch mathematisch manipulieren, um auch nach anderen Variablen aufzulösen.
 ), ist die explizite Formel zum Lösen von an und gibt dir die n-te Zahl der Reihe. Sie können diese Formel jedoch mathematisch manipulieren, um auch nach anderen Variablen aufzulösen.
), ist die explizite Formel zum Lösen von an und gibt dir die n-te Zahl der Reihe. Sie können diese Formel jedoch mathematisch manipulieren, um auch nach anderen Variablen aufzulösen. - Angenommen, Sie kennen das Ende einer Zahlenfolge, möchten aber den Anfang der Zahlenfolge wissen. Dann ordnen Sie die Formel um, um zu erhalten
- Wenn Sie den Start- und Endpunkt einer arithmetischen Folge kennen, aber wissen möchten, wie viele Zahlen die Menge enthält, können Sie die explizite Formel verwenden, um nach n . aufzulösen. Das wird dann
.
- Wenn Sie zuerst die Grundregeln der Algebra durchgehen möchten, die Sie benötigen, um dies berechnen zu können, lesen Sie mehr über Algebra oder einfache algebraische Gleichungen.

2. Finde die erste Zahl einer Reihe. Sie wissen vielleicht, dass die 50. Zahl in einer arithmetischen Folge 300 ist und sich die Zahlen um 7 erhöhen (den Differenzfaktor), aber Sie möchten wissen, was die erste Zahl in der Folge war. Verwenden Sie die modifizierte explizite Formel zum Lösen von a1, um Ihre Antwort herauszufinden.
 und geben Sie alle Informationen ein, die Sie haben. Da Sie wissen, dass die 50. Zahl 300 ist, wissen Sie auch, dass n=50, n-1=49 und a(n)=300. Außerdem ist der Differenzfaktor d angegeben, der 7 . beträgt. Die Formel wird also
und geben Sie alle Informationen ein, die Sie haben. Da Sie wissen, dass die 50. Zahl 300 ist, wissen Sie auch, dass n=50, n-1=49 und a(n)=300. Außerdem ist der Differenzfaktor d angegeben, der 7 . beträgt. Die Formel wird also  . Das wird ausgearbeitet
. Das wird ausgearbeitet  . Die Sequenz, die Sie mit 43 begonnen haben, hat einen Differenzfaktor von 7. Die Sequenz sieht also aus wie 43,50,57,64,71,78…293,300.
. Die Sequenz, die Sie mit 43 begonnen haben, hat einen Differenzfaktor von 7. Die Sequenz sieht also aus wie 43,50,57,64,71,78…293,300.
3. Bestimme die Länge einer Sequenz. Angenommen, Sie wissen, wie die Sequenz beginnt und endet, müssen jedoch herausfinden, wie lang die Sequenz ist. Dann verwende die modifizierte Formel  .
.
 .
. . Wenn du das herausgefunden hast, bekommst du
. Wenn du das herausgefunden hast, bekommst du  , was gleich 212+1 ist, was wiederum 213 . ist. Es gibt 213 Zahlen in dieser Folge.
, was gleich 212+1 ist, was wiederum 213 . ist. Es gibt 213 Zahlen in dieser Folge.Warnungen
- Es gibt verschiedene Arten von Zahlenfolgen. Gehen Sie nicht davon aus, dass eine Menge von Zahlen eine arithmetische Folge ist. Überprüfen Sie immer zwei Zahlenpaare, vorzugsweise drei oder vier, um den Differenzfaktor für die Zahlenmenge zu finden.
Tipps
- Vergiss das nicht D kann entweder positiv oder negativ sein, je nachdem, ob es sich um eine Addition oder eine Subtraktion handelt.
"Bestimmen jedes glieds einer arithmetischen folge"
Оцените, пожалуйста статью