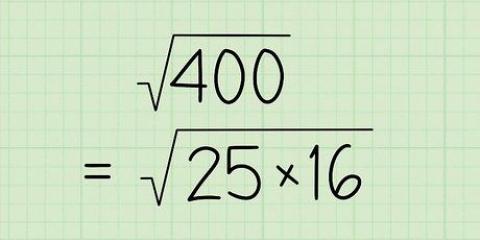Ablesen einer logarithmischen skala

Die meisten Leute sind damit vertraut, Zahlen auf einem Zahlenstrahl zu lesen oder Daten aus einem Diagramm zu lesen. Eine Standardskala ist jedoch unter Umständen nicht sinnvoll. Wenn die Daten exponentiell wachsen oder abnehmen, müssen Sie eine sogenannte logarithmische Skala verwenden. Ein Diagramm der Anzahl der verkauften McDonald`s-Hamburger im Laufe der Zeit würde 1955 bei 1 Million beginnen; als 5 Millionen nur ein Jahr später, dann 400 Millionen, 1 Milliarde (in weniger als 10 Jahren) und bis zu 80 Milliarden im Jahr 1990. Diese Daten wären für eine Standardgrafik zu viel, können aber leicht auf einer logarithmischen Skala dargestellt werden. Wisse, dass eine logarithmische Skala ein anderes System hat, um die Zahlen darzustellen, die nicht wie auf einer Standardskala gleichmäßig verteilt sind. Wenn Sie wissen, wie man eine logarithmische Skala liest, können Sie die Daten effektiver lesen und grafisch darstellen.

Schritte

Methode 1 von 2: Lesen der Achsen des Diagramms

Bild mit dem Titel Read a Logarithmic Scale Step 1
1. Bestimmen Sie, ob eine oder beide Achsen eine Log-Skala verwenden. Grafiken mit schnell wachsenden Daten können Achsen mit einer oder zwei logarithmischen Skalen verwenden. Der Unterschied liegt darin, ob sowohl die x-Achse als auch die y-Achse logarithmische Skalen verwenden oder nur eine. Die Auswahl hängt davon ab, wie viele Details Sie mit der Grafik anzeigen möchten. Wenn die Zahlen auf der einen oder anderen Achse exponentiell wachsen oder abnehmen, möchten Sie möglicherweise eine logarithmische Skala für diese Achse verwenden.
  • Eine logarithmische (oder einfach `log`) Skala hat ungleichmäßige Gitterlinien. Eine Standardskala hat gleichmäßig verteilte Gitterlinien. Einige Daten sollten nur auf Standardpapier gezeichnet werden, andere auf halblogarithmischen Diagrammen und wieder andere auf logarithmischen Diagrammen.
  • Zum Beispiel: Der Graph von ja=x{displaystyle y={sqrt {x}}}{displaystyle y={sqrt {x}}} (oder eine ähnliche Funktion mit einem Quadratwurzelterm) kann auf einem Standardgraphen, einem halblogarithmischen Graphen oder einem loglogarithmischen Graphen aufgetragen werden. In einem Standardgraphen ist die Funktion eine seitwärts gerichtete Parabel, aber die Details für sehr kleine Zahlen sind schwer zu erkennen. Als Log-Log-Diagramm ist die gleiche Funktion eine gerade Linie und die Werte sind weiter verteilt, für mehr Details.
  • Wenn beide Variablen in einer Studie große Datenmengen enthalten, würden Sie wahrscheinlich ein Log-Log-Diagramm verwenden. Studien zu evolutionären Effekten können beispielsweise über Tausende oder Millionen von Jahren gemessen werden, wobei eine logarithmische Skala für die x-Achse angemessen sein könnte. Je nach zu messendem Gegenstand kann eine Log-Log-Skala erforderlich sein.
Bild mit dem Titel Read a Logarithmic Scale Step 2
2. Lesen Sie die Hauptteilungsskala. Auf einer logarithmischen Skala repräsentieren die gleichmäßig verteilten Markierungen die Potenzen der Basis, mit der Sie arbeiten. Die Standardlogarithmen verwenden entweder die Basis 10 oder den natürlichen Logarithmus mit e{displaystyle e}e als Basis.
  • e{displaystyle e}e ist eine mathematische Konstante, die bei der Arbeit mit Zinseszinsen und anderen fortgeschrittenen Berechnungen nützlich ist. Es ist ungefähr gleich 2,718. Dieser Artikel konzentriert sich auf Logarithmen zur Basis 10, aber das Ablesen der natürlichen Logarithmusskala funktioniert auf die gleiche Weise.
  • Standardlogarithmen haben die Basis 10 als Basis. Statt 1, 2, 3, 4... oder 10, 20, 30, 40... oder jede andere Skala mit gleichem Abstand, zählt eine logarithmische Skala mit Potenzen von 10. Die Hauptachsenpunkte sind also, 101,102,103,104{displaystyle 10^{1},10^{2},10^{3},10^{4}}{displaystyle 10^{1},10^{2},10^{3},10^{4}} etc.
  • Jede der Hauptabteilungen, normalerweise mit einer dunkleren Linie auf dem Protokollpapier gekennzeichnet, wird als "Zyklus" bezeichnet. Wenn Sie speziell die Basis 10 verwenden, können Sie den Begriff "Dekade" verwenden, da er sich auf eine neue Potenz von 10 . bezieht.
    • Bild mit dem Titel Read a Logarithmic Scale Step 3
    3. Beachten Sie, dass kleine Intervalle nicht gleichmäßig verteilt sind. Wenn Sie logarithmisches Millimeterpapier verwenden, werden Sie feststellen, dass die Abstände zwischen den Hauptgeräten nicht gleichmäßig verteilt sind. Das heißt, zum Beispiel würde der Marker für 20 tatsächlich etwa 1/3 des Abstands zwischen 10 und 100 . platziert werden.
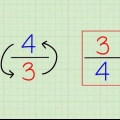
  • Die kleinen Intervalle basieren auf dem Logarithmus jeder Zahl. Wenn also 10 als erster wichtiger Punkt auf der Skala und 100 als zweiter dargestellt wird, liegen die anderen Zahlen wie folgt dazwischen:
  • lÖg(10)=1{displaystyle log(10)=1}{displaystyle log(10)=1}
  • lÖg(20)=1,3{displaystyle log(20)=1,3}{displaystyle log(20)=1,3}
  • lÖg(30)=1,48{displaystyle log(30)=1.48}{displaystyle log(30)=1.48}
  • lÖg(40)=1,60{displaystyle log(40)=1.60}{displaystyle log(40)=1.60}
  • lÖg(50)=1,70{displaystyle log(50)=1.70}{displaystyle log(50)=1.70}
  • lÖg(60)=1,78{displaystyle log(60)=1.78}{displaystyle log(60)=1.78}
  • lÖg(70)=1,85{displaystyle log(70)=1.85}{displaystyle log(70)=1.85}
  • lÖg(80)=1,90{displaystyle log(80)=1.90}{displaystyle log(80)=1.90}
  • lÖg(90)=1,95{displaystyle log(90)=1.95}{displaystyle log(90)=1.95}
  • lÖg(100)=2,00{displaystyle log(100)=2.00}{displaystyle log(100)=2.00}
  • Bei höheren Zehnerpotenzen sind die kleinen Intervalle im gleichen Verhältnis verteilt. Zum Beispiel der Abstand zwischen 10, 20, 30... im Abstand zwischen 100, 200, 300... oder 1000, 2000, 3000...

    • Methode 2 von 2: Punkte auf einer logarithmischen Skala auftragen

    Bild mit dem Titel Read a Logarithmic Scale Step 4
    1. Bestimmen Sie die Art der Waage, die Sie verwenden möchten. Für die folgende Erläuterung liegt der Fokus auf einem halblogarithmischen Graphen mit einer Standardskala für die x-Achse und einer logarithmischen Skala für die y-Achse. Sie können es jedoch möglicherweise umkehren, je nachdem, wie Sie die Daten anzeigen möchten. Das Umkehren der Achsen bewirkt eine Verschiebung des Graphen um neunzig Grad und kann die Interpretation der Daten in die eine oder andere Richtung erleichtern. Darüber hinaus möchten Sie möglicherweise eine Log-Skala verwenden, um bestimmte Datenwerte zu verteilen und deren Details sichtbarer zu machen.
    Bild mit dem Titel Read a Logarithmic Scale Step 5
    2. Markieren Sie den Maßstab der x-Achse. Die x-Achse ist die unabhängige Variable. Die unabhängige Variable ist die Variable, die Sie im Allgemeinen in einer Messung oder einem Experiment kontrollieren. Die unabhängige Variable wird durch die andere Variable in der Studie nicht beeinflusst. Einige Beispiele für unabhängige Variablen sind:
  • Datum
  • Zeit
  • Das Alter
  • Medikamente verabreicht
    • Bild mit dem Titel Read a Logarithmic Scale Step 6
    3. Stellen Sie fest, dass Sie eine logarithmische Skala für die y-Achse benötigen. Sie verwenden eine logarithmische Skala, um Daten abzubilden, die sich extrem schnell ändern. Ein Standarddiagramm ist nützlich für Daten, die linear wachsen oder fallen. Ein logarithmischer Graph ist für Daten, die sich exponentiell ändern. Beispiele für solche Daten sind:
  • Bevölkerungswachstum
  • Verbrauch
  • Zinseszins
    • Bild mit dem Titel Read a Logarithmic Scale Step 7
    4. Beschriften Sie die logarithmische Skala. Überprüfen Sie Ihre Daten und entscheiden Sie, wie Sie die y-Achse markieren. Wenn Ihre Daten nur Zahlen innerhalb von beispielsweise Millionen und Milliarden messen, müssen Sie den Graphen wahrscheinlich nicht bei Null beginnen. Sie können den niedrigsten Zyklus auf dem Diagramm als 106{displaystyle 10^{6}}{displaystyle 10^{6}}. Die nächsten Zyklen werden dann sein 107,108,109{displaystyle 10^{7},10^{8},10^{9}}{displaystyle 10^{7},10^{8},10^{9}} etc.
    Bild mit dem Titel Read a Logarithmic Scale Step 8
    5. Finden Sie die Position auf der x-Achse für einen Datenpunkt. Um den ersten (oder einen beliebigen) Datenpunkt grafisch darzustellen, beginnen Sie mit der Bestimmung seiner Position entlang der x-Achse. Dies kann eine aufsteigende Skala sein, z. B. eine reguläre Zahlenreihe 1, 2, 3 usw. Dabei kann es sich um eine Skala von Beschriftungen handeln, die Sie zuweisen, z. B. Daten oder Monate des Jahres, in denen Sie bestimmte Messungen vornehmen.
    Bild mit dem Titel Read a Logarithmic Scale Step 9
    6. Bestimmen Sie die Position entlang der logarithmischen y-Achse. Sie müssen die entsprechende Position entlang der y-Achse für die Daten finden, die Sie darstellen möchten. Denken Sie daran, da Sie mit einer logarithmischen Skala arbeiten, sind die Hauptnoten Zehnerpotenzen und die Zwischennoten die Unterteilungen. Zum Beispiel: zwischen 106{displaystyle 10^{6}}{displaystyle 10^{6}} (eine Million) und 107{displaystyle 10^{7}}10^{7} (zehn Millionen), die Markierungen repräsentieren Schritte von einer Million.
  • Zum Beispiel: Die Zahl 4.000.000 würde an der vierten kleinen Marke oben aufgetragen werden 106{displaystyle 10^{6}}{displaystyle 10^{6}}. Obwohl 4.000.000 auf einer linearen Standardskala weniger als auf halbem Weg zwischen 1.000.000 und 10.000.000, aufgrund der logarithmischen Skala sieht es tatsächlich nach etwas mehr als der Hälfte aus.
  • Sie müssen bedenken, dass die höheren Intervalle, die näher an der Obergrenze liegen, gequetscht werden. Dies liegt an der mathematischen Natur der logarithmischen Skala.
    • Bild mit dem Titel Read a Logarithmic Scale Step 10
    7. Weiter mit allen Daten. Wiederholen Sie die vorherigen Schritte für alle Daten, die Sie zum Erstellen eines Diagramms benötigen. Ermitteln Sie für jeden Datenpunkt zuerst seine Position entlang der x-Achse und dann seine entsprechende Position entlang der logarithmischen Skala der y-Achse.

    Warnungen

    • Wenn Sie Daten von einer logarithmischen Skala ablesen, stellen Sie sicher, dass Sie wissen, welche Basis für den Logarithmus verwendet wird. Daten, die mit Basis 10 gemessen werden, unterscheiden sich stark von Daten, die auf einer natürlichen logarithmischen Skala mit Basis e . gemessen werden.

    De.FaqCartx.info / Bildung & kommunikation
    Оцените, пожалуйста статью
    Erstellen sie eine silhouette in photoshop
    Erstellen sie eine silhouette in photoshop
    Schienung eines gebrochenen katzenbeins
    Schienung eines gebrochenen katzenbeins
    Halte spinnen von deinem haus fern
    Halte spinnen von deinem haus fern
    Gewinne einen schüchternen jungen für dich
    Gewinne einen schüchternen jungen für dich
    Behandeln sie furunkel zu hause
    Behandeln sie furunkel zu hause
    Pickel austrocknen
    Pickel austrocknen