Die summe einer arithmetischen folge ermitteln

Eine arithmetische Folge ist eine Folge von Zahlen, wobei jede Zahl um einen konstanten Wert ansteigt. Für die Summe einer arithmetischen Folge können Sie alle Zahlen addieren. Dies ist jedoch nicht wirklich praktikabel, wenn die Folge viele Terme enthält. Stattdessen können Sie schnell die Summe jeder arithmetischen Folge finden, indem Sie den Durchschnitt der ersten und letzten Zahl mit der Anzahl der Terme in der Folge multiplizieren.

Schritte

Teil 1 von 3: Analysieren Ihrer Sequenz

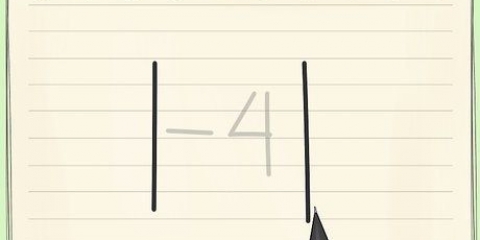
2. Bestimmen Sie die Anzahl der Terme in Ihrer Sequenz. Jede Zahl ist ein Begriff. Wenn nur eine Zahl genannt wird, kannst du sie zählen. Wenn Sie die erste Zahl, die letzte Zahl und den Differenzfaktor (die Differenz zwischen den einzelnen Zahlen) kennen, können Sie die Anzahl der Zahlen mit einer Formel bestimmen. Diese Zahl wird durch die Variable . dargestellt $n$.

Wenn Sie beispielsweise die Summe der Reihen 10, 15, 20, 25, 30 berechnen möchten, dann $n=5$, weil es fünf Zahlen in der Folge gibt.

3. Finden Sie die erste und letzte Zahl in der Folge. Sie müssen beide Zahlen kennen, um die Summe der arithmetischen Folge zu berechnen. Oft ist die erste Zahl eins, aber nicht immer. Setze die Variable ${\mathrm{ein}}_{}$ gleich der ersten Zahl in der Folge, und ${\mathrm{ein}}_{}$ gleich der letzten Zahl in der Folge.

Zum Beispiel in der Reihenfolge 10, 15, 20, 25, 30 ${\mathrm{ein}}_{}$, und ${\mathrm{ein}}_{}$.

Teil 2 von 3: Berechnen Sie die Summe

1. Schreiben Sie die Formel, um die Summe einer arithmetischen Folge zu finden. Die Formel lautet $S_{}$, wodurch $S_{}$ ist gleich der Summe der Reihe.

• Beachten Sie, dass diese Formel anzeigt, dass die Summe der arithmetischen Folge gleich dem Durchschnitt der ersten und letzten Zahl multipliziert mit der Anzahl der Zahlen ist.

2. Geben Sie die Werte ein $$n{displaystyle n}, $$ein1{displaystyle a_{1}} und $$einn{displaystyle a_{n}} in der Formel in. Stellen Sie sicher, dass Sie richtig ersetzen.

Wenn Ihre Sequenz beispielsweise fünf Zahlen enthält, wobei 10 die erste Zahl und 30 die letzte Zahl ist, sieht Ihre Formel wie folgt aus: $S_{}$.

Zum Beispiel:
$S_{}$
$S_{}$

Zum Beispiel:
$S_{}$
$S_{}$
Also ist die Summe der Reihe (10, 15, 20, 25, 30) gleich 100.

Teil 3 von 3: Vervollständigen der Beispielaufgaben

Bestimmen Sie die Anzahl der Zahlen ($n$) in der Serie. Da Sie mit drei beginnen, mit 24 aufhören und jedes Mal sieben hinzufügen, ist die Zahlenfolge 3, 10, 17, 24. (Der Differenzfaktor ist die Differenz zwischen jeder Zahl in der Reihe.) Das bedeutet, dass $n=4$

Bestimmen Sie die erste (${\mathrm{ein}}_{}$) und zuletzt (${\mathrm{ein}}_{}$) Zahl in der Reihenfolge. Da die Sequenz 3 bis 24 ist, ${\mathrm{ein}}_{}$ und ${\mathrm{ein}}_{}$.

Finden Sie den Mittelwert von ${\mathrm{ein}}_{}$ und ${\mathrm{ein}}_{}$: $$.

Multiplizieren Sie den Mittelwert mit $n$: $13,5\times 4=54$.

Bestimmen Sie die Anzahl der Terme ($n$) in der Serie. Weil Mara 52 Wochen spart, (1 Jahr), $n=52$.

Bestimmen Sie die erste (${\mathrm{ein}}_{}$) und zuletzt (${\mathrm{ein}}_{}$) Zahl in der Reihenfolge. Der erste Betrag, den sie spart, sind fünf Euro, also ${\mathrm{ein}}_{}$. Um den Gesamtbetrag zu berechnen, der in der letzten Woche des Jahres gespart wurde, berechnen wir $5\times 52=260$. Also ${\mathrm{ein}}_{}$.

Bestimmt den Mittelwert von ${\mathrm{ein}}_{}$ und ${\mathrm{ein}}_{}$: $$.

Multiplizieren Sie den Mittelwert mit $n$: $135,5\times 52=6890$. Also hat sie am Ende des Jahres 6890 € gespart.

"Die summe einer arithmetischen folge ermitteln"

Bestimmen jedes glieds einer arithmetischen folge

Ermitteln der anzahl der terme in einer arithmetischen folge

Den definitionsbereich einer funktion ermitteln

Ermitteln des medians einer reihe von zahlen