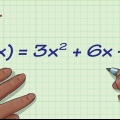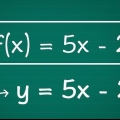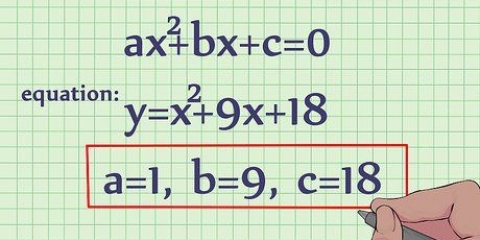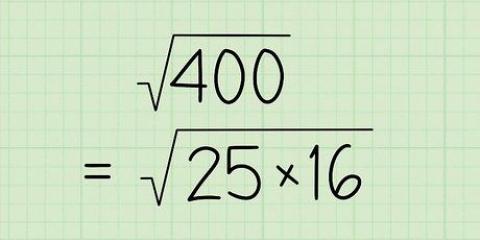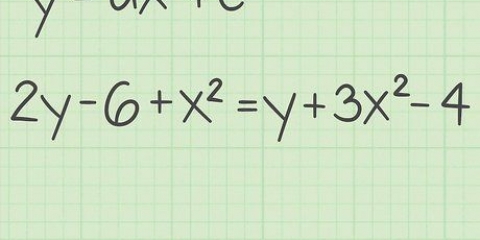Ein Polynom ohne Nullstellen oder Brüche mit Variablen im Nenner. Der Definitionsbereich dieser Art von Funktionen besteht aus der Menge aller reellen Zahlen. Eine Funktion mit einem Bruch mit einer Variablen im Nenner. Um den Bereich dieser Art von Funktion zu finden, setzen Sie den Nenner des Bruchs gleich Null und ignorieren Sie den x-Wert, den Sie nach der Lösung der Gleichung finden. Eine Funktion mit einer Variablen innerhalb eines Radikals. Um den Bereich dieser Art von Funktion zu finden, setzen Sie die Terme innerhalb des Radikals größer als 0 und lösen Sie die Gleichung, um herauszufinden, welche Werte für x innerhalb dieser Funktion korrekt sind. Eine Funktion mit natürlichem Logarithmus (ln). Machen Sie die Begriffe in Klammern >0 und lösen. Ein Graph. Leiten Sie aus der Grafik ab, welche Werte für x . richtig sind. Ein Verhältnis. Dies ist eine Liste von x- und y-Koordinaten. Ihre Domain ist einfach eine Liste von x-Koordinaten. 
Die Struktur einer Domäne ist eine offene eckige/runde Klammer, gefolgt von den 2 Endpunkten der Domäne, getrennt durch ein Komma und gefolgt von einer schließenden eckigen/runden Klammer. Zum Beispiel: [-1.5). Dies bedeutet, dass die Domäne von -1 bis 5 . geht. Verwenden Sie eckige Klammern wie [ und ] um anzuzeigen, ob eine Zahl in einen bestimmten Bereich fällt. Im Beispiel [-1.5) fällt also -1 in den Bereich. Verwenden Sie Klammern wie ( und ) um anzuzeigen, dass eine Nummer außerhalb einer bestimmten Domäne liegt. Im Beispiel [-1.5) liegt die 5 also außerhalb der Domäne. Die Domain endet an jedem Punkt vor der 5, zum Beispiel 4.999… Verwenden Sie „U“ (bedeutet "Union") um voneinander getrennte Teile der Domäne zu verbinden.` Zum Beispiel: [-1.5) U (5.10]. Dies bedeutet, dass die Domäne von -1 bis 10 reicht, aber es gibt eine Lücke in der Domäne bei 5. Dies könnte zum Beispiel an einer Funktion mit „x - 5“ im Nenner liegen. du kannst so viel machen "SIE"-Verwenden Sie nach Bedarf Symbole, wenn die Domäne mehrere Umbrüche hat. Verwenden Sie das Unendlich-Symbol (in positiver und negativer Richtung), um anzuzeigen, dass die Domäne in dieser Richtung unendlich ist. Verwenden Sie bei unendlich immer ( ) und nicht [ ]. 

f(x) = 2x/(x - 4) x - 4 = 0 (x - 2 )(x + 2) = 0 x ≠ (2, - 2) 
x = alle reellen Zahlen außer 2 und -2 

x-7 0 
x 7 
D = [7,∞) 
Überprüfen Sie nun den Bereich unter -2 (z.B. durch. -3), ob dies ein Ergebnis größer Null ergibt. Stimmt. (-3) - 4 = 5 Überprüfen Sie nun den Bereich zwischen -2 und 2. Nehmen Sie zum Beispiel 0. 0 - 4 = -4, also wissen Sie, dass die Zahlen zwischen -2 und 2 nicht funktionieren. Versuchen Sie es jetzt mit einer Zahl über 2, z. B. +3. 3 - 4 = 5, also die Zahlen über 2 funktionieren. Schreiben Sie die Domain auf, wenn Sie fertig sind. So schreiben Sie dies auf: D = (-∞, -2) U (2, ∞) 

x - 8 > 0 
x - 8 + 8 > 0 + 8 x > 8 
D = (8,∞) 

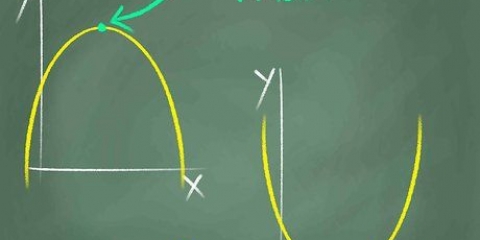
Eine Linie. Wenn Sie eine Linie im Graphen sehen, die ins Unendliche geht, wird schließlich jeder x-Wert in der Parabel enthalten sein, sodass der Definitionsbereich gleich allen reellen Zahlen ist. Eine gewöhnliche Parabel. Wenn Sie eine nach oben oder unten zeigende Parabel sehen, dann besteht der Definitionsbereich aus allen reellen Zahlen, da alle Zahlen auf der x-Achse letztlich in der Parabel enthalten sind. Eine horizontale Parabel. Handelt es sich um eine Parabel mit dem Scheitelpunkt (4,0), die sich unendlich nach rechts erstreckt, dann ist Ihr Definitionsbereich gleich D = [4,∞) 




Den definitionsbereich einer funktion ermitteln
- Schritte
- Methode 1 von 6: Die Grundlagen lernen
- Methode 2 von 6: Den Definitionsbereich einer Funktion finden, die einen Bruch enthält
- Methode 3 von 6: Den Definitionsbereich einer Funktion mit einer Quadratwurzel ermitteln
- Methode 4 von 6: Bestimmung des Definitionsbereichs einer Funktion mit dem natürlichen Logarithmus
- Methode 5 von 6: Den Definitionsbereich einer Funktion mithilfe eines Graphen ermitteln
- Methode 6 von 6: Bestimmung des Definitionsbereichs einer Funktion anhand einer Sammlung/Beziehung
Der Definitionsbereich einer Funktion ist eine Sammlung von Zahlen, die in diese Funktion passen. Mit anderen Worten, es ist eine Sammlung von x-Werten, die einer bestimmten Gleichung zugeordnet sind. Die Menge der y-Werte heißt Funktionsumfang. Wenn Sie wissen möchten, wie Sie die Domäne einer Funktion in verschiedenen Situationen finden, gehen Sie wie folgt vor.
Schritte
Methode 1 von 6: Die Grundlagen lernen

1. Lernen Sie die Definition einer Domain. Ein Bereich einer Funktion ist definiert als die Menge aller reellen Zahlen, die als Eingaben für diese Funktion dienen können. Mit anderen Worten, eine Domäne ist die vollständige Menge von x-Werten, die in eine Funktion eingegeben werden, was zu einer Menge von y-Werten führt.

2. Erfahren Sie, wie Sie die Domäne verschiedener Funktionen finden. Die Art der Funktion bestimmt die beste Methode, um eine Domäne zu finden. Hier sind die Grundlagen, die Sie für die folgenden Funktionen benötigen:

3. Die Notation einer Domain verstehen. Die korrekte Schreibweise einer Domäne ist leicht zu erlernen, aber es ist wichtig, dass Sie dies richtig machen, um keine Punkte in Tests und Prüfungen zu verpassen. Hier sind ein paar Dinge, die Sie wissen müssen, um die Domäne einer Funktion korrekt zu schreiben:
Methode 2 von 6: Den Definitionsbereich einer Funktion finden, die einen Bruch enthält

1. Schreibe die Aufgabe. Angenommen, Sie haben folgendes Problem:
- f(x) = 2x/(x - 4)

2. Bei Brüchen mit einer Variablen im Nenner setzt man diese Variable in einer Gleichung gleich null. Wenn Sie den Definitionsbereich einer Funktion mit einem Bruch finden möchten, schließen Sie alle x-Werte aus, die den Nenner gleich Null machen, da Sie niemals durch Null teilen können. Schreiben Sie den Nenner als Gleichung und setzen Sie ihn gleich 0. So geht`s:

3. Notieren Sie sich die Domain. So geht`s:
Methode 3 von 6: Den Definitionsbereich einer Funktion mit einer Quadratwurzel ermitteln

1. Schreibe die Aufgabe. Angenommen, Sie haben das folgende Problem: Y = (x-7)

2. Stellen Sie sicher, dass die Terme innerhalb der Quadratwurzel größer oder gleich 0 . sein dürfen. Sie können nicht die Quadratwurzel einer negativen Zahl ziehen, aber Sie können die Quadratwurzel von Null ziehen. Beachten Sie, dass dies nicht nur für Quadratwurzeln gilt, sondern für alle geraden Wurzelzahlen. Sie gilt nicht für ungerade Radikalzahlen, da es kein Problem darstellt, wenn eine negative Zahl unter dem Radikalzeichen steht. Hier ist ein Beispiel:

3. Isolieren Sie die Variable. Um nun x auf der linken Seite der Gleichung zu trennen, addieren Sie 7 zu beiden Seiten des Gleichheitszeichens, so dass es nach dieser Operation so aussieht:

4. Schreiben Sie die Domain richtig. Dies ist die richtige Schreibweise:

5. Finden Sie den Definitionsbereich einer Funktion mit einer Quadratwurzel, wenn mehrere Lösungen möglich sind. Angenommen, Sie haben die folgende Funktion: y = 1/√( ̅x -4). Wenn Sie den Nenner außerhalb der Klammern nehmen und ihn gleich Null setzen, erhalten Sie x ≠ (2, - 2). So gehen Sie vor:
Methode 4 von 6: Bestimmung des Definitionsbereichs einer Funktion mit dem natürlichen Logarithmus

1. Schreibe die Aufgabe. Angenommen, Sie haben dies:
- f(x) = ln(x-8)

2. Machen Sie die Terme in den Klammern größer als Null. Der natürliche Logarithmus muss positiv sein, also machen Sie die Terme in den Klammern größer als Null. Hier ist ein Beispiel:

3. Lösen. Trennen Sie die Variable x durch Addieren von 8 zu beiden Seiten der Gleichung. Hier ist wie:

4. Notieren Sie sich die Domain. Zeigen Sie, dass der Definitionsbereich dieser Gleichung gleich allen Zahlen größer als 8 bis unendlich ist. Hier ist wie:
Methode 5 von 6: Den Definitionsbereich einer Funktion mithilfe eines Graphen ermitteln

1. Sehen Sie sich das Diagramm an.

2. Untersuche, welche x-Werte zum Graphen gehören. Das ist leichter gesagt als getan, deshalb hier ein paar Tipps:

3. Bestimmen Sie die Domäne. Bestimmen Sie die Domäne basierend auf der Art des Diagramms, das Sie haben. Wenn Sie sich nicht ganz sicher sind, aber die Geradengleichung kennen, geben Sie die x-Koordinaten in die Funktion ein, um sie zu überprüfen.
Methode 6 von 6: Bestimmung des Definitionsbereichs einer Funktion anhand einer Sammlung/Beziehung

1. Schreibe die Beziehung auf. Eine Relation ist einfach eine Reihe von x- und y-Koordinaten. Angenommen, Sie haben die folgenden Koordinaten: {(1, 3), (2, 4), (5, 7)}

2. Schreibe die x-Koordinaten auf. Diese sind: 1, 2, 5.

3. Bestimmen Sie die Domäne. D = {1, 2, 5}

4. Stellen Sie sicher, dass diese Beziehung eine Funktion ist. Eine Relation ist eine Funktion, wenn Sie jedes Mal, wenn Sie eine numerische x-Koordinate eingeben, dieselbe y-Koordinate als Antwort erhalten. Wenn Sie also eine 3 vor das x setzen, erhalten Sie 6 als y-Wert und so weiter. Die nächste Beziehung ist nicht eine Funktion, weil Sie für jeden Wert von zwei verschiedene y-Werte erhalten "x": {(1, 4),(3, 5),(1, 5)}.
"Den definitionsbereich einer funktion ermitteln"
Оцените, пожалуйста статью