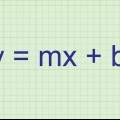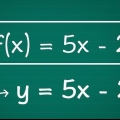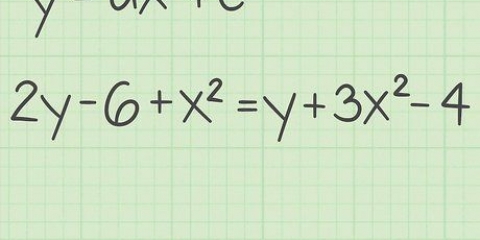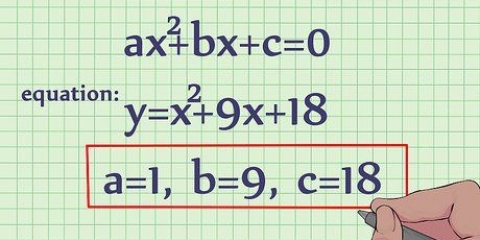Verarbeite dann -1 in der Funktion, um die y-Koordinate zu erhalten. f(-1) = 3(-1) + 6(-1) -2 = 3 - 6 -2 = -5. Der Scheitelpunkt der Parabel ist (-1,-5). Verarbeiten Sie dies in der Grafik, indem Sie einen Punkt an der x-Koordinate -1 und y-Koordinate -5 . zeichnen. Dies sollte im dritten Quadranten des Graphen sein. 
f(-2) = 3(-2) + 6(-2) -2 = -2. Ein Punkt in der Grafik ist (-2, -2) f(0) = 3(0) + 6(0) -2 = -2. Ein weiterer Punkt in der Grafik ist (0,-2) f(1) = 3(1) + 6(1) -2 = 7. Ein dritter Punkt im Diagramm ist (1, 7). 



Aber angenommen y = -3 ist der tiefste Punkt des Graphen, steigt aber ewig an. Dann ist der Bereich f(x) ≥ -3, und nicht mehr. Angenommen, der Graph erreicht seinen höchsten Punkt bei y=10, fällt dann aber für immer weiter. Dann ist der Bereich f(x) ≤ 10. 






Zum Beispiel: Wenn sie 2 Tickets verkauft, müssen Sie 2 mit 5 multiplizieren, mit 10 als Antwort und somit der Gesamtsumme. 

Das heißt, jede positive ganze Zahl, die ein Vielfaches von fünf ist, ist ein mögliches Ergebnis der Funktion.
Bestimmung des umfangs einer funktion
- Schritte
- Methode 1 von 4: Bestimmen des Wertebereichs einer Funktion mit einer gegebenen Gleichung
- Methode 2 von 4: Den Bereich einer Funktion anhand eines Graphen bestimmen
- Methode 3 von 4: Bestimmen des Umfangs der Funktion einer Beziehung
- Methode 4 von 4: Bestimmen Sie den Umfang einer Funktion in einem Problem
- Tipps
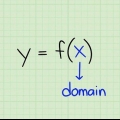
Der Bereich einer Funktion ist die Menge von Zahlen, die die Funktion erzeugen kann. Mit anderen Worten, es ist die Menge der y-Werte, die Sie erhalten, wenn Sie alle möglichen x-Werte in die Funktion einbeziehen. Diese Menge von x-Werten wird als Domäne bezeichnet. Wenn Sie wissen möchten, wie Sie den Bereich einer Funktion berechnen, führen Sie die folgenden Schritte aus.
Schritte
Methode 1 von 4: Bestimmen des Wertebereichs einer Funktion mit einer gegebenen Gleichung

1. Schreibe die Gleichung auf. Angenommen, Sie haben die folgende Gleichung: f(x) = 3x + 6x -2. Das bedeutet, dass bei der Eingabe eines Wertes für die x der Gleichung, dass Sie dann a ja-bekommt Wert. Dies ist die Funktion einer Parabel.

2. Finden Sie den Scheitelpunkt der Funktion, wenn es sich um eine quadratische Gleichung handelt. Wenn Sie eine Gerade oder eine Funktion mit einem Polynom oder einer ungeraden Zahl haben, z. B. f(x) = 6x+2x + 7, können Sie diesen Schritt überspringen. Aber wenn Sie es mit einer Parabel oder einer Gleichung zu tun haben, bei der die x-Koordinate quadriert oder um eine gerade Potenz erhöht wird, müssen Sie den Scheitelpunkt der Parabel zeichnen. Verwenden Sie dazu die Gleichung -b/2a für die x-Koordinate der Funktion 3x + 6x -2, wobei 3 = a, 6 = b und -2 = c. In diesem Fall, -B ist -6 und 2a ist 6, also ist die x-Koordinate -6/6 oder -1.

3. Finden Sie einige andere Punkte der Funktion. Um ein Gefühl für die Funktion zu bekommen, solltest du noch einige andere Werte für x eingeben, damit du dir ein Bild davon machen kannst, wie die Funktion aussieht, bevor du mit der Suche nach dem Bereich beginnst. Da es sich um eine Parabel handelt und x positiv ist, zeigt die Parabel nach oben (Talparabel). Aber um sicher zu gehen, geben wir noch ein paar Werte für x ein, um zu sehen, welche y-Koordinaten sie ergeben:

4. Finden Sie den Bereich des Diagramms. Betrachten Sie nun die y-Koordinaten des Graphen und finden Sie den tiefsten Punkt, an dem der Graph die y-Koordinate berührt. In diesem Fall liegt die niedrigste y-Koordinate am oberen Rand der Parabel, -5 und der Graph erstreckt sich unendlich über diesen Punkt hinaus. Dies bedeutet, dass der Funktionsumfang y = alle reellen Zahlen ≥ -5.
Methode 2 von 4: Den Bereich einer Funktion anhand eines Graphen bestimmen

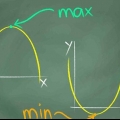
1. Finden Sie das Minimum der Funktion. Finden Sie die niedrigste y-Koordinate der Funktion. Angenommen, die Funktion erreicht ihren tiefsten Punkt bei -3. Diese Funktion kann bis ins Unendliche immer kleiner werden, hat also keinen festen Tiefstpunkt - nur Unendlich.

2. Finden Sie das Maximum der Funktion. Angenommen, die höchste y-Koordinate der Funktion ist 10. Diese Funktion kann auch unendlich groß werden, hat also keinen festen Höchstpunkt - nur unendlich.

3. Geben Sie die Reichweite an. Dies bedeutet, dass der Bereich der Funktion oder der Bereich der y-Koordinaten von -3 bis 10 . beträgt. Also -3 ≤ f(x) ≤ 10. Das ist der Umfang der Funktion.
Methode 3 von 4: Bestimmen des Umfangs der Funktion einer Beziehung

1. Schreibe die Beziehung auf. Eine Relation ist eine Menge geordneter Paare von x- und y-Koordinaten. Sie können sich eine Beziehung ansehen und ihre Domäne und ihren Umfang bestimmen. Angenommen, Sie haben es mit folgender Beziehung zu tun: {(2, –3), (4, 6), (3, –1), (6, 6), (2, 3)}.

2. Listen Sie die y-Koordinaten der Beziehung auf. Um den Bereich der Beziehung zu bestimmen, schreiben wir alle y-Koordinaten jedes geordneten Paares auf: {-3, 6, -1, 6, 3}.

3. Entfernen Sie alle doppelten Koordinaten, sodass Sie nur eine von jeder y-Koordinate haben. Sie haben vielleicht bemerkt, dass Sie die "6" zweimal in der Liste. Entfernen Sie das, sodass {-3, -1, 6, 3} übrig bleibt.

4. Schreiben Sie den Bereich der Beziehung in aufsteigender Reihenfolge. Ordne dann die Zahlen im Set vom kleinsten zum größten und du hast den Bereich gefunden. Der Bereich der Relation {(2, –3), (4, 6), (3, –1), (6, 6, (2, 3)} ist {-3,-1, 3, 6}. Du bist fertig.

5. Machen Sie die Beziehung zu einer Funktion ist. Damit eine Relation eine Funktion ist, muss jedes Mal, wenn Sie eine Zahl von einer x-Koordinate eingeben, die y-Koordinate gleich sein. Zum Beispiel ist die Beziehung {(2, 3) (2, 4) (6, 9)} Nein Funktion, denn wenn Sie die 2 zum ersten Mal als x eingeben, erhalten Sie eine 3 als Wert, aber wenn Sie das zweite Mal eine 2 eingeben, erhalten Sie vier. Eine Relation ist nur dann eine Funktion, wenn Sie für eine bestimmte Eingabe immer die gleiche Ausgabe erhalten. Wenn Sie -7 eingeben, sollten Sie jedes Mal die gleiche y-Koordinate (was auch immer das sein mag) erhalten.
Methode 4 von 4: Bestimmen Sie den Umfang einer Funktion in einem Problem

1. Lesen Sie die Ausgabe. Angenommen, Sie arbeiten an folgendem Problem: "Becky verkauft Tickets für die Talentshow ihrer Schule für jeweils 5 US-Dollar. Der Gesamtbetrag, den sie sammelt, hängt von der Anzahl der von ihr verkauften Tickets ab. Was ist der Funktionsumfang?"

2. Schreiben Sie das Problem als Funktion. In diesem Fall m der eingezogene Betrag und T die Anzahl der verkauften Tickets. Da jedes Ticket 5 Euro kostet, müssen Sie die Anzahl der verkauften Tickets mit 5 multiplizieren, um den Gesamtbetrag zu erhalten. Daher kann die Funktion geschrieben werden als M(t) = 5t.

3. Bestimmen Sie, was die Domäne ist. Um den Bereich zu finden, benötigen Sie zuerst die Domain. Die Domäne besteht aus allen möglichen Werten von t, die an der Gleichung teilnehmen. In diesem Fall kann Becky 0 oder mehr Tickets verkaufen – sie kann keine negative Anzahl von Tickets verkaufen. Da wir die Anzahl der Plätze in der Aula der Schule nicht kennen, können wir davon ausgehen, dass sie theoretisch unendlich viele Karten verkaufen kann. Und sie kann nur ganze Tickets verkaufen, nicht einen Teil davon. Daher ist der Definitionsbereich der Funktion T = jede positive ganze Zahl.

4. Bestimmen Sie die Reichweite. Die Spanne ist der mögliche Betrag, den Becky mit dem Verkauf aufbringen kann. Sie müssen mit der Domäne arbeiten, um den Bereich zu finden. Wenn Sie wissen, dass der Definitionsbereich aus einer positiven ganzen Zahl besteht und die Gleichung M(t) = 5t Dann wissen Sie auch, dass Sie in diese Funktion eine beliebige positive ganze Zahl für die Antwort oder den Bereich eingeben können. Zum Beispiel: Wenn sie 5 Tickets verkauft, dann ist M(5) = 5 x 5 oder 25 Euro. Wenn sie 100 verkauft, dann ist M(100) = 5 x 100 oder 500 Euro. Daher ist der Funktionsumfang jede positive ganze Zahl, die ein Vielfaches von fünf ist.
Tipps
- Sehen Sie, ob Sie die Umkehrung der Funktion finden können. Der Bereich der Inversen einer Funktion ist gleich dem Bereich dieser Funktion.
- In den schwierigeren Fällen kann es einfacher sein, den Graphen zuerst mit der Domäne zu zeichnen (falls erforderlich) und dann den Bereich aus dem Graphen abzulesen.
- Überprüfen Sie, ob die Funktion wiederholt wird. Jede Funktion, die sich entlang der x-Achse wiederholt, hat den gleichen Bereich für die gesamte Funktion. Zum Beispiel: f(x) = sin(x) hat einen Bereich zwischen -1 und 1.
Оцените, пожалуйста статью