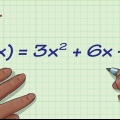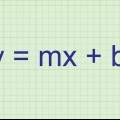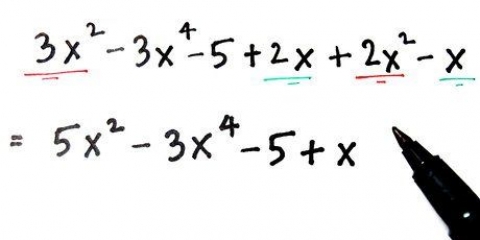Die Ableitung eines Exponenten ist der Exponent mal die -1 Potenz einer Zahl. Die Ableitung von x ist also 5x und die Ableitung von x ist 3.5x. Wenn vor dem x bereits eine Zahl steht, multiplizieren Sie diese mit dem Exponenten. Zum Beispiel: die Ableitung von 3x ist 12x. Die Ableitung einer beliebigen Konstanten ist null. Die Ableitung von 8 ist also 0. Die Ableitung einer Summe ist die Summe jeder einzelnen Ableitung. Zum Beispiel: die Ableitung von x + 3x ist 3x + 6x. Die Ableitung eines Produkts ist der erste Faktor mal die Ableitung des zweiten Faktors plus der zweite Faktor mal die Ableitung des ersten. Zum Beispiel ist die Ableitung von x(2x + 1) x(2) + (2x + 1)3x, was gleich 8x + 3x . ist. Die Ableitung eines Quotienten (sagen wir f/g) ist [g(Ableitung von f) - f(Ableitung von g)]/g. Zum Beispiel: die Ableitung von (x + 2x - 21)/(x - 3) ist (x - 6x + 15)/(x - 3). 






Bestimmung eines derivats
Ableitungen können verwendet werden, um nützliche Eigenschaften eines Graphen zu bestimmen, wie Maxima, Minima, Spitzen und Täler und Steigungen. Sie können sie sogar verwenden, um komplexe Gleichungen ohne Grafikrechner zu zeichnen! Leider ist die Bestimmung der Ableitung einer Gleichung oft eine schwierige Aufgabe, aber dieser Artikel hilft Ihnen mit einer Reihe von Tipps und Tricks.
Schritte

1. Verstehe die Notation eines Derivats. Die folgenden zwei Arten der Notation sind die gebräuchlichsten, aber zahlreiche andere Möglichkeiten finden Sie auf Wikipedia.
- Leibniz-Notation Diese Notation wird am häufigsten verwendet, wenn die Gleichung ay und x . enthält. Dy/dx bedeutet wörtlich "die Ableitung von y nach x". Versuchen Sie es sich als Δy/Δx für die Werte von x und y vorzustellen, wobei die Differenz verschwindend klein ist. Diese Erklärung gibt natürlich die Definition eines Grenzwertes bezüglich der Ableitung: limh->0 (f(x+h)-f(x))/h. Wenden Sie diese Notation auf die zweite Ableitung an, schreiben Sie: dy/dx.
- Lagranges Notation Die Ableitung einer Funktion f wird auch geschrieben als f`(x). Diese Notation wird ausgesprochen als "die Funktion f von x". Diese Notation ist kürzer als die von Leibniz und wird verwendet, wenn eine Ableitung als Funktion betrachtet wird. Für höhere Ableitungen füge einfach eine weitere hinzu " ` " bereit für "F", die zweite Ableitung wie f``(x) aussehen lassen.

2. Verstehen Sie, was ein Derivat ist und wofür es verwendet wird. Um die Steigung eines linearen Graphen zu ermitteln, werden zunächst zwei Punkte auf der Geraden genommen und diese Koordinaten in die Gleichung (y2 - ja1)/(X2 - x1). Dies ist jedoch nur mit linearen Graphen möglich. Bei quadratischen Gleichungen und höher ist der Graph eine Kurve, daher ist die Differenz zwischen zwei Punkten nicht genau genug. Um die Steigung einer Tangente einer Parabel zu bestimmen, werden zwei Punkte genommen und in die Gleichung eingetragen, um die Steigung einer gekrümmten Linie zu bestimmen: [f(x + dx) - f(x)]/dx. Dx bedeutet"Delta x," was ist der Unterschied zwischen den beiden x-Koordinaten der beiden Punkte des Graphen. Beachten Sie, dass diese Gleichung dieselbe ist wie (y2 - ja1)/(X2 - x1), aber in anderer Form. Da bereits bekannt ist, dass das Ergebnis nicht genau sein wird, wird eine indirekte Näherung gewählt. Um die Steigung der Tangente am Punkt (x, f(x)) zu finden, muss dx gegen 0 gehen, damit die beiden gewählten Punkte fast gleich sind.Aber du kannst nicht durch 0 teilen, also musst du nach dem Einfüllen der Werte der beiden Punkte dedx im Nenner eliminieren. Wenn dies erfolgreich ist, machen Sie dx gleich 0 und lösen Sie. Dies ist die Steigung der Tangente bei (x, f(x)). Die Ableitung einer Gleichung ist die allgemeine Gleichung zum Bestimmen der Steigung einer beliebigen Tangente eines Graphen. Dies mag sehr schwierig erscheinen, aber die folgenden Beispiele zeigen Ihnen, wie Sie die Ableitung bestimmen.
Methode 1 von 4: Explizite Differenzierung

1. Verwenden Sie explizite Differentiation, wenn y bereits auf einer Seite der Gleichung steht.

2. Ersetze eine Gleichung in eine andere Gleichung [f(x + dx) - f(x)]/dx. Zum Beispiel die Gleichung y = x, deren Ableitung [(x + dx) - x]/dx . ist.

3. Erweitere dx weiter, um die Gleichung [dx(2x + dx)]/dx . zu erhalten. Jetzt ist es möglich, das dx im Zähler und Nenner zu eliminieren. Das Ergebnis ist 2x + dx, und wenn sich dx 0 nähert, wird die Ableitung 2x. Dies ist die Steigung einer beliebigen Tangente an den Graphen y = x ist 2x. Geben Sie einfach den Wert eines gegebenen Punktes x ein, dessen Tangens Sie in die Gleichung finden möchten.

4. Lerne, die Muster der gleichen Art von Gleichungen zu erkennen. Unten findet ihr einige.
Methode 2 von 4: Implizite Differenzierung

1. Verwenden Sie implizite Differentiation, wenn Ihre Gleichung nicht einfach mit dem y auf einer Seite des Gleichheitszeichens geschrieben werden kann. Selbst wenn Sie es mit dem y auf einer Seite schreiben, wäre die Berechnung von dy/dx immer noch eine lästige Pflicht. Unten ist ein Beispiel für die Lösung dieser Art von Gleichung.

2. In diesem Beispiel xy + 2y = 3x + 2y, ersetze jey durch f(x), damit klar ist, dass dies tatsächlich eine Funktion ist. Die Gleichung wird dann xf(x) + 2[f(x)] = 3x + 2f(x).

3. Um die Ableitung dieser Gleichung zu finden, differenzieren Sie (ein beeindruckendes Wort für das Finden der Ableitung) Ihre beiden Seiten der Gleichung in Bezug auf x. Die Gleichung wird dann xf`(x) + 2xf(x) + 6[f(x)]f`(x) = 3 + 2f`(x).

4. Ersetze f(x) wieder durch y. Achten Sie darauf, dies nicht mit f`(x) zu tun, da sich dies stark von f(x) unterscheidet.

5. Löse nach f`(x) auf. Die Antwort dieses Beispiels ist (3 - 2xy)/(x + 6y - 2).
Methode 3 von 4: Höhere Derivate

1. Die höhere Ableitung einer Funktion zu nehmen bedeutet nur die Ableitung der Ableitung zu nehmen. Wenn zum Beispiel nach der dritten Ableitung gefragt wird, nehmen Sie die Ableitung der Ableitung der Ableitung. Bei einigen Gleichungen wird eine höhere Ableitung gleich 0.
Methode 4 von 4: Die Kettenregel

1. Wenn y eine differenzierbare Funktion von z und z eine differenzierbare Funktion von x ist, dann ist y eine zusammengesetzte Funktion von x und die Ableitung von y nach x (dy/dx) ist (dy/du)*(du /dx). Die Kettenregel kann auch eine zusammengesetzte Gleichung sein, wie folgt: (2x - x). Um die Ableitung davon zu finden; Denke einfach so wie du es mit der Produktlinie machst. Multiplizieren Sie die Gleichung mit dem Exponenten und reduzieren Sie den Exponenten um 1. Dann multiplizieren Sie die Gleichung mit der Ableitung, die unter den Exponenten fällt (in diesem Fall 2x^4 - x). Die Antwort auf dieses Problem lautet dann 3(2x - x)(8x - 1).
Tipps
- Wenn Sie ein scheinbar unlösbares Problem sehen, machen Sie sich keine Sorgen. Versuchen Sie, das Problem in kleinere Teile zu unterteilen, indem Sie die Produktregeln, die Quotientenregel usw. anwenden. Dann differenziere die einzelnen Teile.
- Üben Sie die Produktregel, Quotientenregel, Kettenregel und vor allem die implizite Differentiation, da diese von der Infinitesimalrechnung ziemlich knifflig sein können.
- Kennen Sie Ihren Taschenrechner; Probieren Sie die verschiedenen Funktionen Ihres Taschenrechners aus, um zu erfahren, wie sie funktionieren. Es ist sicherlich wertvoll zu wissen, wie man die Tangens- und Ableitungsfunktionen verwendet, wenn Ihr Taschenrechner sie hat.
- Merken Sie sich die am häufigsten verwendeten trigonometrischen Ableitungen und wie Sie damit arbeiten.
Warnungen
- Denken Sie daran, dass das Minuszeichen vor dem f(Ableitung oder g) steht, wenn Sie die Quotientenregel verwenden; Dies ist ein häufiger Fehler und führt zu einer falschen Antwort.
Оцените, пожалуйста статью