Den Rangkorrelationskoeffizienten von Spearman berechnen

Schritte
Tipps
Warnungen

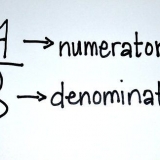
Mit dem Rangkorrelationskoeffizienten von Spearman können Sie sehen, ob zwei Variablen durch eine monotone Funktion (d.w.z. dass wenn eine Zahl zunimmt, auch die andere Zahl zunimmt oder umgekehrt). Um den Rangkorrelationskoeffizienten von Spearman zu berechnen, müssen Sie Datensätze ordnen und vergleichen, um Σd zu finden, und dann diesen Wert in die Standard- oder vereinfachte Version der Formel für den Rangkorrelationskoeffizienten von Spearman eingeben. Sie können diesen Koeffizienten auch mit Excel-Formeln oder R-Befehlen berechnen.

Schritte

Methode 1 von 3: Manuell

1. Zeichnen Sie Ihre Datentabelle. Organisiert die Informationen, die Sie zur Berechnung des Rangkorrelationskoeffizienten nach Spearman benötigen. Du brauchst:

6 Spalten mit Überschriften, wie oben gezeigt.
So viele Zeilen, wie Sie Datenpaare haben.

2. Füllen Sie die ersten beiden Spalten mit Ihren Datenpaaren.

3. Ordnen Sie die Datenpunkte der ersten Spalte in der dritten Spalte an, von 1 bis n (die Gesamtzahl der Datenpunkte, die Sie haben). Geben Sie die niedrigste Zahl Position 1, die nächste Zahl Position 2 usw.

4. Machen Sie dasselbe mit der vierten Spalte wie in Schritt 3, aber ordnen Sie jetzt die zweite Spalte an.

Wenn Sie zwei (oder mehr) Datenpunkte mit demselben Wert in einer Spalte haben, nehmen Sie den Durchschnitt der Positionen, die diese Datenpunkte normalerweise haben würden, und geben Sie den Datenpunkten diesen Durchschnitt als ihre neue Position an.
Im Beispiel rechts gibt es zwei Fünfer, die normalerweise auf Position 2 und 3 liegen würden. Es sind zwei gleiche Lieder, also nimm den Durchschnitt ihrer Positionen. Der Mittelwert von 2 und 3 ist 2,5, also geben Sie beiden Fünfen die Position 2,5.

5. Berechnen Sie in der Spalte `d` die Differenz zwischen den beiden Positionen in jedem Datenpaar. Mit anderen Worten, wenn einer Position 1 und der andere Position 3 hat, beträgt die Differenz 2. (Positiv oder negativ spielt keine Rolle, da wir diesen Unterschied im nächsten Schritt quadrieren werden.)

6. Quadrieren Sie die Werte in der Spalte d und schreiben Sie diese Werte in die Spalte d.

7. Addiere alle Datenpunkte in der Spalte d zusammen. Dieser Wert ist Σd.

8. Wählen Sie eine der folgenden Formeln:

Wenn in den vorherigen Schritten keine gleichen Datenpunkte aufgetreten sind, geben Sie Σd in die einfache Formel für den Rangkorrelationskoeffizienten nach Spearman ein

und geben Sie die Anzahl der Datenpaare für `n` ein, um Ihre Antwort zu finden.

Wenn in den vorherigen Schritten ähnliche Datenpunkte aufgetreten sind, verwenden Sie die Standardformel für den Rangkorrelationskoeffizienten nach Spearman:

9. Interpretiere das Ergebnis. Dies kann zwischen -1 und 1 . variieren.

Nahe bei -1 – negative Korrelation.

Nahe 0 – Keine lineare Korrelation.

Nahe bei 1 – Positive Korrelation.

Methode 2 von 3: In Excel

1. Erstellen Sie neue Spalten mit den Positionen der vorhandenen Spalten. Wenn Sie beispielsweise Ihre Daten in Spalte A2:A11 haben, würden Sie die Formel `=RANK(A2,A$2:A$11)` verwenden und den Bereich auf alle Ihre Zeilen und Spalten erweitern.

2. Behandeln Sie gleiche Datenpunkte wie in den Schritten 3 und 4 von Methode 1 beschrieben.

3. Führen Sie in einer neuen Zelle eine Korrelationsberechnung zwischen den beiden Spalten mit einer Formel wie `=KORREL(C2:C11,D2:D11)` durch. In diesem Fall sind C und D die Positionsspalten. Der Rangkorrelationskoeffizient von Spearman erscheint in der Korrelationszelle.

Methode 3 von 3: Mit R

1. Installiere R, falls du es noch nicht hast. (Sehen https://www.r-Projekt.Organisation/.)

2. Speichern Sie Ihre Daten als CSV-Datei mit den Daten, die Sie in den ersten beiden Spalten korrelieren möchten. Sie können dies mit dem Menü "Speichern unter" tun.

3. Öffne den R-Editor. Wenn Sie im Terminal arbeiten, führen Sie einfach R . aus. Wenn Sie sich auf Ihrem Desktop befinden, klicken Sie auf das R-Logo.

4. Geben Sie die folgenden Befehle ein:

D <- lesen.csv("NAME_OF_YOU_CSV.csv") und drücken Sie die Eingabetaste

cor(Rang(d[,1]),Rang(d[,2]))

Tipps

Für die meisten Datensätze benötigen Sie mindestens fünf Datenpaare, um einen Trend zu ermitteln (im Beispiel wurden nur drei Paare verwendet, um das Beispiel zu vereinfachen).

Warnungen

Der Rangkorrelationskoeffizient nach Spearman zeigt nur dann die Korrelationsstärke, wenn die Datenpunkte kontinuierlich ansteigen oder abfallen. Wenn das Streudiagramm der Datenpunkte einen anderen Trend zeigt, erhöht der Rangkorrelationskoeffizient von Spearman die Korrelation nicht richtig anzeigen.
Diese Formel basiert auf der Annahme, dass es keine gleichen Datenpunkte gibt. Bei gleichen Datenpunkten, wie im obigen Beispiel, verwenden Sie die folgende Definition: den Produkt-Moment-Korrelationskoeffizienten für die Ränge.