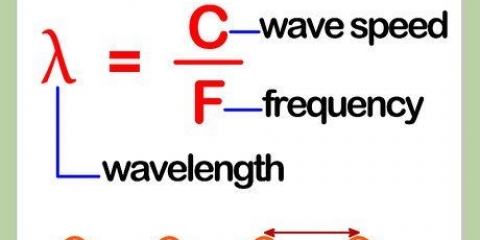
Mittelpunkt der Wippe = 4 Meter vom Nullpunkt entfernt. Kind 1=1 Meter vom Nullpunkt entfernt Kind 2=5 Meter vom Nullpunkt entfernt 



430 m*kg ÷ 130 Kilo=3,31 m Der Schwerpunkt liegt 3,31 Meter vom Nullpunkt oder vom Nullpunkt gemessen 3,31 Meter vom Ende der linken Seite der Wippe, wo der Nullpunkt platziert wurde. 



So wie wir es gelöst haben, ist die Null auf der linken Seite der Wippe. Unsere Antwort ist 3,31 m, also ist unser Massenschwerpunkt 3,31 m von der Null auf der linken Seite entfernt. Wenn Sie einen neuen Nullpunkt wählen, 1 m von links, erhalten Sie als Antwort 2,31 m vom Massenmittelpunkt entfernt. Der Massenschwerpunkt beträgt 2,31 m vom neuen Nullpunkt, d.h. 1 m von links. Der Massenschwerpunkt beträgt 2,31 + 1 = 3,31 m von links, und daher die gleiche Antwort wie wir vorher berechnet haben. (Hinweis: Denken Sie bei der Entfernungsmessung daran, dass Entfernungen links vom Nullpunkt sind negativ und Abstände Rechts davon positiv.) 
Bei Wippenproblemen kommt es nur darauf an, wo der Schwerpunkt von links nach rechts entlang der Wippenlinie liegt. Später erfahren Sie vielleicht, wie Sie den Schwerpunkt in zwei Dimensionen berechnen können.
Berechnen sie den schwerpunkt
Der Schwerpunkt (der Massenmittelpunkt) ist der Mittelpunkt der Gewichtsverteilung eines Objekts – der Punkt, an dem die Schwerkraft auf dieses Objekt einwirkt. Dies ist der Punkt, an dem das Objekt in perfekter Balance ist, egal wie das Objekt um diesen Punkt verdreht oder gedreht wird. Wenn Sie wissen möchten, wie man den Schwerpunkt eines Objekts berechnet, benötigen Sie das Gewicht des Objekts und aller darauf befindlichen Objekte. Dann bestimmen Sie eine Nullstelle und verarbeiten die bekannten Größen in der Gleichung, um den Schwerpunkt eines Objekts oder Systems zu berechnen. Wenn Sie wissen möchten, wie Sie den Schwerpunkt berechnen, befolgen Sie die folgenden Schritte.
Schritte
Methode 1 von 4: Bestimmen Sie das Gewicht

1. Berechnen Sie das Gewicht des Objekts. Bei der Berechnung des Schwerpunkts müssen Sie zunächst das Gewicht des Objekts ermitteln. Angenommen, Sie möchten das Gewicht einer Wippe mit einer Masse von 30 kg berechnen. Da es sich um ein symmetrisches Objekt handelt, liegt sein Schwerpunkt genau in der Mitte (wenn niemand darauf sitzt). Aber wenn auf der Wippe Leute mit unterschiedlichen Massen sind, dann wird das Problem etwas komplizierter.

2. Berechnen Sie die zusätzlichen Gewichte. Um den Schwerpunkt der Wippe mit zwei Kindern darauf zu bestimmen, müssen Sie das individuelle Gewicht jedes Kindes ermitteln. Das erste Kind wiegt 40 Kilo und das zweite Kind 60 Kilo.
Methode 2 von 4: Bestimmen Sie den Nullpunkt

1. Wählen Sie einen Nullpunkt. Der Nullpunkt ist ein beliebiger Startpunkt auf einer Seite der Wippe. Sie können die Null auf einer Seite der Wippe oder auf der anderen Seite platzieren. Nehmen wir an, die Wippe ist 6 Meter lang. Setzen wir die Null auf die linke Seite der Wippe, in die Nähe des ersten Kindes.

2. Messen Sie den Abstand vom Nullpunkt zum Mittelpunkt des Hauptobjekts sowie zu den beiden Zusatzgewichten. Nehmen wir an, die Kinder sind jeweils 1 Meter von jedem Ende der Wippe entfernt. Die Mitte der Wippe ist die Mitte der Wippe oder 3 Meter, da 6 Meter geteilt durch 2 gleich 3 . sind. Hier die Abstände vom Zentrum des größten Objekts und die beiden Zusatzgewichte bilden den Nullpunkt:
Methode 3 von 4: Bestimmen Sie den Schwerpunkt

1. Multiplizieren Sie die Entfernung jedes Objekts zum Nullpunkt mit seinem Gewicht, um den Moment zu finden. So hast du den Moment für jedes Objekt. So multiplizieren Sie den Abstand jedes Objekts vom Nullpunkt mit seinem Gewicht:
- Die Wippe: 30 Kilo x 3 m=90 m*kg.
- Kind 1=40 Kilo x 1 m=40 m*kg.
- Kind 2=60 Kilo x 5 m=300 m*kg.

2. Füge die drei Momente zusammen. Berechnen Sie einfach folgendes: 90 m*kg + 40 m*kg + 300 m*kg=430 m*kg. Das Gesamtmoment beträgt 430 m*kg.

3. Addiere die Gewichte aller Objekte zusammen. Finden Sie die Summe der Gewichte der Wippe und der beiden Kinder. Gehen Sie dabei wie folgt vor: 30 Kilo + 40 Kilo + 60 Kilo = 130 Kilo.

4. Teilen Sie das Gesamtmoment durch das Gesamtgewicht. Ermittelt den Abstand vom Nullpunkt zum Schwerpunkt des Objekts. Dies durch Division von 430 m * kg durch 130 kg.
Methode 4 von 4: Überprüfen Sie Ihre Antwort

1. Finden Sie den Schwerpunkt im Diagramm. Wenn der gefundene Schwerpunkt außerhalb des Objektsystems liegt, dann haben Sie die falsche Antwort gefunden. Vielleicht haben Sie die Entfernung von mehr als einem Punkt berechnet. Versuche es noch einmal mit nur einem Nullpunkt.
- Bei Personen, die beispielsweise auf der Wippe sitzen, sollte der Schwerpunkt irgendwo auf der Wippe liegen, nicht links oder rechts von der Wippe. Es muss nicht an einer Person liegen.
- Dies gilt auch für Probleme in zwei Dimensionen. Zeichne ein Quadrat, das gerade groß genug ist, um alle Objekte in deinem Problem aufzunehmen. Der Schwerpunkt muss innerhalb dieses Quadrats liegen.

2. Überprüfen Sie Ihre Berechnungen, wenn Ihre Antwort zu klein ist. Wenn Sie ein Ende des Systems als Nullpunkt gewählt haben, dann platziert eine kleine Antwort den Schwerpunkt direkt neben einem Ende. Dies mag die richtige Antwort sein, aber es ist oft ein Hinweis darauf, dass etwas schief gelaufen ist. Hast du das Gewicht und den Abstand zueinander in der Berechnung multipliziert? So findest du diesen Moment. Wenn Sie versehentlich zusammengefügt, dann bekommst du wahrscheinlich eine viel kleinere antwort.

3. Überprüfen Sie Ihre Berechnung, wenn Sie mehr als einen Schwerpunkt gefunden haben. Jedes System hat nur einen einzigen Schwerpunkt. Wenn es mehr sind, haben Sie möglicherweise den Schritt übersprungen, in dem Sie alle Momente zusammenzählen mussten. Der Schwerpunkt ist es gesamt Moment geteilt durch die gesamt Gewicht. Du musst nicht jeder Moment zum Teilen von jeder Gewicht, das Ihnen nur die Position jedes Objekts angibt.

4. Kreuzen Sie die Null an, wenn Ihre Antwort eine ganze Zahl ist. Die Antwort in unserem Beispiel ist 3,31 m Angenommen, Sie erhalten 2,31 m, 4,31 m oder eine andere Zahl, die auf ` endet.31.Dies liegt wahrscheinlich daran, dass wir das linke Ende der Wippe als Nullpunkt gewählt haben, während Sie das rechte Ende oder einen anderen Punkt in ganzzahliger Entfernung von unserer Nullpunkt gewählt haben. Ihre Antwort ist richtig, unabhängig von der gewählten Null! Das musst du dir nur merken die Null steht immer für x=0. Hier ist ein Beispiel:

5. Stellen Sie sicher, dass alle Ihre Messungen gerade Linien sind. Angenommen, Sie sehen ein anderes Beispiel mit "Kinder auf einer Wippe", aber ein Kind ist viel größer als das andere, oder ein Junge hängt unter der Wippe, anstatt darauf zu sitzen. Ignoriere den Unterschied und nimm alle deine Messungen entlang der geraden Linie der Wippe. Das Messen von Entfernungen in einem Winkel liefert Antworten, die nahe beieinander liegen, aber leicht unterschiedlich sind.
Tipps
- Um die Distanz zu bestimmen, die eine Person zurücklegen muss, um die Wippe auf der Stütze auszubalancieren, verwenden Sie diese Formel: (bewegt Gewicht) / (Gesamtgewicht)=(Entfernung, über die sich der Schwerpunkt verschoben hat) / (Strecke, über die das Gewicht bewegt wurde). Diese Formel kann umgeschrieben werden, um zu zeigen, dass die Entfernung, die das Gewicht (die Person) bewegt werden muss, gleich der Entfernung zwischen dem Schwerpunkt und dem Drehpunkt ist, mal das Gewicht der Person geteilt durch das Gesamtgewicht. Das muss das erste Kind auch -1,31 m * 40 Kilo / 130 Kilo =-0.40 m bewegen (bis zum Ende der Wippe). Oder sollte das zweite Kind -1.08 m *130 Kilo / 60 Kilo=-2.84 m bewegen. (zur Mitte der Wippe).
- Um den Schwerpunkt eines zweidimensionalen Objekts zu finden, verwenden Sie die Formel Xcg=∑xW/∑W, um den Schwerpunkt entlang der x-Achse zu finden, und Ycg=∑yW/∑W, um den Schwerpunkt entlang der y-Achse zu finden, um zu finden. Der Schnittpunkt ist der Schwerpunkt.
- Die Definition des Schwerpunkts einer allgemeinen Massenverteilung ist (∫ r dW/∫ dW) wobei dW gleich der Ableitung des Gewichts, r der Ortsvektor ist und die Integrale als Stieltjes-Integrale über das Ganze zu interpretieren sind Karosserie. Sie können jedoch als konventionellere Riemann- oder Lebesgue-Volumenintegrale für Verteilungen mit einer Wahrscheinlichkeitsdichtefunktion ausgedrückt werden. Ausgehend von dieser Definition lassen sich alle Eigenschaften des Schwerpunkts, auch die in diesem Artikel verwendeten, aus den Eigenschaften von Stieltjes-Integralen ableiten.
Warnungen
- Versuchen Sie nicht blindlings, diese Mechanik anzuwenden, ohne die Theorie zu verstehen, was zu Fehlern führen kann. Versuchen Sie zunächst, die zugrunde liegenden Gesetze/Theorien zu verstehen.
"Berechnen sie den schwerpunkt"
Оцените, пожалуйста статью