Geschwindigkeit ist das Maß dafür, wie schnell etwas in einem bestimmten Moment geht. Wenn Sie jemals während der Fahrt auf den Tachometer eines Autos geschaut haben, haben Sie gesehen, wie Geschwindigkeit gemessen wird – je weiter die Nadel geht, desto höher ist die Geschwindigkeit des Autos. Es gibt verschiedene Möglichkeiten, die Geschwindigkeit zu berechnen, je nachdem, welche Informationen Sie haben. Für allgemeine Zwecke lautet die Gleichung Geschwindigkeit = Distanz/Zeit (oder s = a/t) normalerweise der einfachste Weg, um die Geschwindigkeit zu berechnen.
Schritte
Methode 1 von 3: Verwenden der Standardgeschwindigkeitsgleichung
1.
Finden Sie die Entfernung, die ein Objekt zurückgelegt hat. Die grundlegende Gleichung, die die meisten Leute verwenden, um herauszufinden, wie schnell etwas geht, ist sehr einfach zu verwenden. Das erste, was Sie wissen müssen, ist
wie weit das Objekt zurückgelegt hat. Mit anderen Worten, wie weit ist der Startpunkt vom Endpunkt entfernt??
- Diese Gleichung wird an einem Beispiel leichter zu verstehen sein. Nehmen wir an, wir fahren mit dem Auto zu einem Themenpark von 100 Meilen (ca. 161 Kilometer). In den nächsten Schritten werden wir diese Informationen verwenden, um diese Gleichung zu lösen.
2. Finden Sie die Zeit heraus, die das Objekt benötigt hat, um diese Entfernung zurückzulegen. Die nächste Information, die Sie brauchen, ist wie lange brauchte das Objekt, um zu reisen. Mit anderen Worten, wie lange hat es gedauert, um vom Startpunkt zum Endpunkt zu gelangen??
Sagen wir in unserem Beispiel, dass es genau so ist zwei Uhr Kosten für diese Reise.3. Teilen Sie die Entfernung durch die Zeit, um die Geschwindigkeit zu ermitteln. Alles, was Sie brauchen, sind diese beiden Informationen, um Ihre Geschwindigkeit für die Fahrt zu bestimmen. Die Distanz etwa die Zeit gibt dir die Geschwindigkeit des Objekts an.
In unserem Beispiel lautet diese Gleichung 100 Meilen/2 Stunden = 50 Meilen/Stunde(ca. 80km/h).4. Vergiss die Einheiten nicht. Beschriften Sie Ihre Antwort mit den entsprechenden Einheiten (z. B. Meilen pro Stunde usw.).) ist kritisch. Ohne Einheiten kann es für andere Personen schwierig sein zu verstehen, was Ihre Antwort bedeutet. Sie können auch Punkte verlieren, wenn Sie vergessen, die Einheit auf einer Schulaufgabe aufzuschreiben.
Die Einheiten für die Geschwindigkeit sind die Entfernungseinheiten über die Zeiteinheiten. In unserem Beispiel sind unsere Einheiten Meilen/Stunde (oder Meilen pro Stunde), da wir die Entfernung in Meilen und die Zeit in Stunden gemessen haben.Methode 2 von 3: Andere Probleme lösen
1.
Isolieren Sie die verschiedenen Variablen, um Entfernung und Zeit zu berechnen. Sobald Sie die Grundlagen der Geschwindigkeitsgleichung kennen, können Sie sie verwenden, um mehr als nur die Geschwindigkeit zu finden. Wenn Sie beispielsweise die Geschwindigkeit und eine der anderen Variablen kennen, können Sie die Gleichung neu anordnen, um die fehlende Information zu finden.
- Angenommen, wir wissen, dass ein Zug vier Stunden lang mit einer Geschwindigkeit von 20 Stundenkilometern gefahren ist, aber wir müssen die Entfernung kennen, die er zurückgelegt hat. In diesem Fall können wir die Gleichung neu anordnen und folgendermaßen lösen:
- Geschwindigkeit = Distanz/Zeit
- Geschwindigkeit × Zeit = (Entfernung/Zeit) × Zeit
- Geschwindigkeit × Zeit = Entfernung
- 20 km/h × 4 h = Distanz = 80 Kilometer

2. Konvertieren Sie Ihre Einheiten bei Bedarf. Manchmal können Sie die Geschwindigkeit in einer anderen Einheit berechnen, als Sie benötigen. In diesem Fall solltest du Umrechnungsfaktoren Verwenden Sie, um Ihre Antwort in die richtige Einheit zu setzen. Schreibe dazu die Beziehungen zwischen deinen Einheiten als Bruch und multipliziere. Wenn Sie multiplizieren, drehen Sie Ihren Bruch nach Bedarf, um die Einheiten loszuwerden, die Sie nicht möchten. Das ist viel einfacher als es klingt!
Nehmen wir zum Beispiel an, dass wir in der obigen Beispielaufgabe unsere Antwort in benötigen Meilen anstatt Kilometer. Eine Meile hat ungefähr 1,6 Kilometer, also können wir sie wie folgt umrechnen:
- 80 Kilometer × 1 Meile/1.6 Kilometer = 50 Meilen
Beachten Sie, dass, da Kilometer am unteren Rand des Bruchs stehen, dieser mit den Kilometern in der ursprünglichen Antwort durchgestrichen werden kann, sodass die Antwort in Meilen bleibt.Dieses Website enthält Umrechnungen für die gängigsten Einheiten.3. Ersetze die Variable `Abstand` bei Bedarf durch Distanzformeln. Objekte bewegen sich nicht immer in schönen, bequemen geraden Linien. Wenn nicht, können Sie möglicherweise nicht einfach einen numerischen Wert für die Entfernung in die Standardgeschwindigkeitsgleichung einfügen. Stattdessen müssen Sie möglicherweise a in s = a/t durch eine Formel ersetzen, die die Entfernung modelliert, die das Objekt zurückgelegt hat.
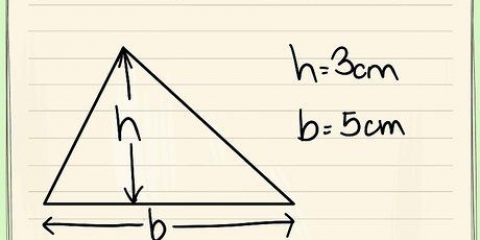
Nehmen wir zum Beispiel an, ein Flugzeug fliegt fünfmal in einem Kreis mit einer Breite von 32 km. Das Flugzeug absolviert diese Reise in einer halben Stunde. In diesem Beispiel müssen wir noch genau bestimmen, wie weit das Flugzeug geflogen ist, bevor wir die Geschwindigkeit ermitteln können. Wir können die Gleichung für die Entfernung um einen Kreis (seinen Umfang) anstelle von verwenden "ein" in unserem Vergleich. Diese Gleichung lautet Umfang = 2πr wobei r = der Radius des Kreises. Wir können dies wie folgt lösen:
- s = (2 × π × r)/t
- s = (2 × π × 10)/0.5
- s = 62.83/0.5 = 125.66 Meilen/Stunde

4. Sehen Sie, dass s = a/t a Durchschnitt Geschwindigkeit gibt. Die einfache, bequeme Gleichung, mit der wir die Geschwindigkeit ermittelt haben, hat einen großen Fehler. Der Wert, den es gibt, ist technisch eine Durchschnittsgeschwindigkeit. Dies bedeutet, dass es davon ausgeht, dass das Objekt, das Sie messen hat während der gesamten Fahrt die gleiche Geschwindigkeit. Wie wir weiter unten sehen werden, kann es schwieriger sein, die Geschwindigkeit eines Objekts zu einem bestimmten Zeitpunkt zu bestimmen.
Um diesen Unterschied zu veranschaulichen, stellen Sie sich Ihre letzte Fahrt mit dem Auto vor. Es ist sehr unwahrscheinlich, dass Sie die gesamte Fahrt mit der gleichen Geschwindigkeit gefahren sind. Stattdessen hast du langsam angefangen und nach und nach deine Höchstgeschwindigkeit erreicht und an Ampeln, Staus usw. abgebremst. Wenn Sie die Standardgeschwindigkeitsgleichung verwenden, um Ihre Geschwindigkeit für die Fahrt zu berechnen, werden diese Geschwindigkeitsänderungen nicht berücksichtigt. Stattdessen erhalten Sie eine Antwort irgendwo zwischen den verschiedenen Geschwindigkeiten, mit denen Sie gefahren sind.Methode 3 von 3: Berechnung der Momentangeschwindigkeit
Anmerkung: In diesem Abschnitt werden Techniken verwendet, die denen unbekannt sind, die sich nicht mit der Analysis vertraut gemacht haben. Hilfe finden Sie in unseren Artikeln zur Infinitesimalrechnung.

1.
Beachten Sie, dass Geschwindigkeit als Betrag der Geschwindigkeit definiert ist. Geschwindigkeitsberechnungen auf höherer Ebene können verwirrend sein, da Mathematiker und Wissenschaftler unterschiedliche Definitionen für "Geschwindigkeit" verwenden. Eine Geschwindigkeit (Geschwindigkeit) hat zwei Komponenten: a
Größe und ein
Richtung. Die Größe ist gleich der Geschwindigkeit des Objekts. Eine Richtungsänderung bewirkt eine Geschwindigkeitsänderung (Geschwindigkeit), jedoch keine Geschwindigkeitsänderung.
- Nehmen wir zum Beispiel an, zwei Autos fahren in entgegengesetzte Richtungen. Die Tachos beider Autos zeigen 50 km/h an, also haben beide die gleiche Geschwindigkeit. Da sie sich jedoch auseinander bewegen, können wir sagen, dass ein Auto ein Geschwindigkeit) von -50 km/h und man hat a Geschwindigkeit) ab 50 km/h.
- So wie Sie die Momentangeschwindigkeit (Geschwindigkeit) berechnen können, können Sie auch die Momentangeschwindigkeit (Geschwindigkeit) berechnen.

2. Verwenden Sie absolute Werte für negative Geschwindigkeiten. Objekte können negative Geschwindigkeiten haben (wenn sie sich relativ zu etwas anderem in eine negative Richtung bewegen). Es gibt jedoch keine negative Geschwindigkeit (Geschwindigkeit), daher ist in diesen Fällen die absoluter Wert der Größe ändert die Geschwindigkeit des Objekts.
Aus diesem Grund haben beide Autos im obigen Beispielproblem a Geschwindigkeit (Geschwindigkeit) durch 50 km/h.3. Nehmen Sie die Ableitung einer Positionsfunktion. Wenn Sie eine Funktion s(t) haben, die Ihnen die Position eines Objekts in Bezug auf die Zeit angibt, dann gibt Ihnen die Ableitung von s(t) Geschwindigkeit) zeitlich geben. Setzen Sie einfach einen Zeitwert in diese Gleichung für die Variable t ein (oder was auch immer der Zeitwert ist), um die Geschwindigkeit an diesem Punkt zu erhalten. Von hier aus ist es einfach, die Geschwindigkeit zu finden.
Angenommen, die Position eines Objekts in Metern ist durch die Gleichung 3t + t - 4 gegeben, wobei t = Zeit in Sekunden. Wir wollen wissen, wie schnell das Objekt bei t = 4 Sekunden ist. In diesem Fall können wir dies wie folgt lösen:
- 3t + t - 4
- s`(t) = 2 × 3t + 1
- s`(t) = 6t + 1
Nun setzen wir t = 4 ein:
- s`(t) = 6(4) + 1 = 24 + 1 = 25 Meter/Sekunde. Dies ist technisch gesehen eine Geschwindigkeitsmessung (Geschwindigkeit), aber da sie positiv ist und die Richtung im Problem nicht erwähnt wird, können wir sie im Wesentlichen für die Geschwindigkeit verwenden.
4. Nehmen Sie das Integral einer Beschleunigungsfunktion. Beschleunigung ist ein Weg, um Änderung der Geschwindigkeit eines Objekts im Laufe der Zeit messen. Dieses Thema ist etwas zu komplex, um es in diesem Artikel vollständig zu erklären. Es ist jedoch nützlich zu beachten, dass das Integral von a(t) eine Geschwindigkeit (Geschwindigkeit) in Bezug auf die Zeit liefert, wenn Sie eine Funktion a(t) haben, die eine Beschleunigung in Bezug auf die Zeit angibt. Beachten Sie, dass es hilfreich ist, die Anfangsgeschwindigkeit des Objekts zu kennen, damit Sie die Konstante definieren können, die sich aus einem unbestimmten Integral ergibt.
Angenommen ein Objekt hat eine konstante Beschleunigung (in m/s gegeben durch a (t) = -30. Nehmen wir auch an, das Objekt hat eine Anfangsgeschwindigkeit von 10 m/s. Wir müssen die Geschwindigkeit bei t = 12s . finden. In diesem Fall können wir dies wie folgt lösen:
- a(t) = -30
- v(t)= ∫ a(t)dt =∫ -30dt = -30t + C
Um C zu finden, lösen wir nach v(t) für t = 0. Denken Sie daran, dass die Anfangsgeschwindigkeit des Objekts 10 m/s beträgt.
- v(0) = 10 = -30(0) + C
- 10 = C, also v(t) = -30t + 10
Jetzt können wir t = 12 Sekunden eingeben.
- v(12) = -30(12) + 10 = -360 + 10 = -350. Da die Geschwindigkeit der Absolutwert der Geschwindigkeit ist, ist die Geschwindigkeit des Objekts 350 Meter/Sekunde.
Tipps
- Übung macht den Meister! Versuchen Sie, Ihre eigenen Summen zu bilden, indem Sie in den Beispielaufgaben oben verschiedene Zahlen einsetzen.
- Wenn Sie nach einer schnellen Berechnungsmethode für erweiterte Geschwindigkeitsberechnungen suchen, verwenden Sie Hier als der Online-Derivate-Rechner und der Online-Integral-Rechner Hier.
"Geschwindigkeit berechnen"