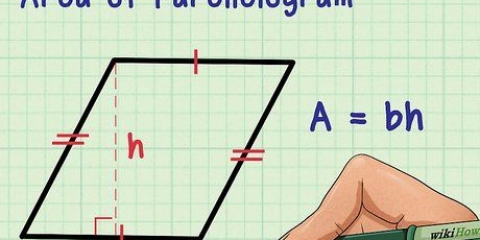Kostenlose Schritt für Schritt Anweisungen 
Fläche = 1/2 x (3cm x 5cm) 
Fläche = 1/2 x (3cm x 5cm) Oberfläche = 1/2 x 15 cm Fläche = 7.5 cm 
Fläche = {6 (6 - 3)(6 - 4)(6 - 5)} 
6 - 3 = 3 6 - 4 = 2 6 - 5 = 1 Fläche = √{6 (3)(2)(1)} 
Fläche = 1/2(b)(c) x sin A Fläche = 1/2(150)(231) x sin A 
Fläche = 1/2(150)(231) x sin A Fläche = 1/2(34.650) x sin A Fläche = 17,325 x sin A Fläche = 17.325 x .8386705 Fläche = 14,530 cm²
Berechnen sie die fläche eines dreiecks
Obwohl die gängigste Methode zur Berechnung der Fläche eines Dreiecks darin besteht, seine halbe Basis mit seiner Höhe zu multiplizieren, gibt es je nach verfügbaren Daten eine Reihe anderer Möglichkeiten, die Fläche eines Dreiecks zu berechnen. Dazu gehören die Länge aller drei Seiten, die Länge einer Seite eines gleichseitigen Dreiecks und die Länge zweier Seiten zusammen mit dem eingeschlossenen Winkel. Lesen Sie hier, wie Sie mit diesen Daten die Fläche eines Dreiecks berechnen können.
Schritte
Methode 1 von 4: Mit der Basis und der Höhe
1. Bestimmen Sie die Basis und Höhe Ihres Dreiecks. Die Basis des Dreiecks ist die Länge einer Seite, die normalerweise die Unterseite des Dreiecks ist. Höhe ist die Länge von der Basis bis zur oberen Ecke des Dreiecks, die senkrecht zur Basis steht. In einem rechtwinkligen Dreieck sind die Basis und die Höhe die beiden Seiten, die sich in einem 90-Grad-Winkel treffen. Aber in einem anderen Dreieck, wie unten zu sehen, schneidet die Höhenlinie direkt durch die Form.
- Sobald Sie die Basis und Höhe des Dreiecks bestimmt haben, können Sie die Formel verwenden.
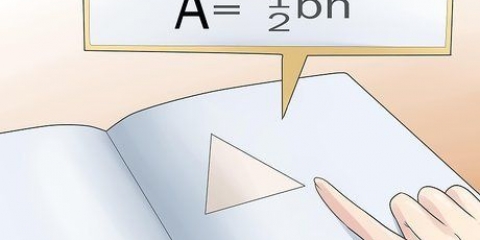
2. Schreiben Sie die Formel auf, um die Fläche eines Dreiecks zu finden. Die Formel für diese Art von Problem lautet Fläche = 1/2 (Basis x Höhe), oder 1/2 (BH). Wenn Sie sich alles notiert haben, können Sie mit dem Ausfüllen der Länge der Höhe und der Basis beginnen.
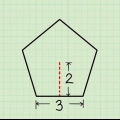
3. Basis- und Höhenwerte eingeben. Finden Sie die Basis und Höhe des Dreiecks und verwenden Sie diese Werte in der Gleichung. In diesem Beispiel beträgt die Höhe des Dreiecks 3 cm und die Basis des Dreiecks 5 cm. So würde die Formel nach Eingabe dieser Werte aussehen:
4. Löse die Gleichung. Sie können zuerst die Höhe mit der Basis multiplizieren, da diese Werte in Klammern stehen. Dann multiplizierst du das Ergebnis mit 1/2. Denken Sie daran, dass Sie die Antwort in Quadratmetern angeben, da Sie im zweidimensionalen Raum arbeiten. So lösen Sie dies für die endgültige Antwort:
Methode 2 von 4: Verwenden der Länge jeder Seite (Reiherformel)
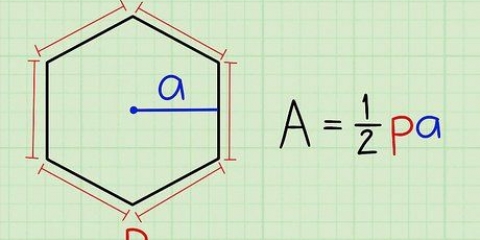
1. Berechnen Sie den halben Umfang (Semiperimeter) des Dreiecks. Um den halben Umfang des Dreiecks zu finden, musst du nur alle Seiten zusammenzählen und das Ergebnis durch zwei teilen. Die Formel zum Ermitteln des halben Umfangs eines Dreiecks lautet wie folgt: Semiperimeter = (Länge der Seite a + Länge der Seite b + Länge der Seite c) / 2, oder s = (a + b + c) / 2. Da alle drei Längen des rechtwinkligen Dreiecks gegeben sind, 3 cm, 4 cm und 5 cm, können Sie diese direkt in die Formeln einsetzen und das Problem für den halben Umfang lösen:
- s = (3 + 4 + 5)/2
- s = 12/2
- s = 6
2. Geben Sie die richtigen Werte in die Formel ein, um die Fläche eines Dreiecks zu finden. Diese Formel zum Ermitteln der Fläche eines Dreiecks wird auch Heronsche Formel genannt und geht so: Fläche = √{s (s - a)(s - b)(s - c)}. Wir wiederholen den vorherigen Schritt, wobei S der halbe Umfang ist und ein, B, und C die drei Seiten des Dreiecks. Verwenden Sie die folgende Reihenfolge von Operationen: zuerst alles innerhalb der Klammern lösen, dann alles unter dem Wurzelzeichen und schließlich die Quadratwurzel selbst. So sieht diese Formel aus, wenn Sie alle bekannten Werte eingegeben haben:
3. Subtrahiere die Werte in den Klammern. Also: 6 - 3, 6 - 4 und 6 - 5. Hier das Ergebnis auf Papier:
4. Multiplizieren Sie die Ergebnisse dieser Operationen. Multiplizieren Sie 3 x 2 x 1, um 6 als Antwort zu erhalten. Sie müssen diese Zahlen miteinander multiplizieren, bevor Sie sie mit 6 multiplizieren, da sie in Klammern stehen.
5. Multiplizieren Sie das vorherige Ergebnis mit dem halben Umfang. Dann multiplizieren Sie das Ergebnis, 6, mit dem halben Umfang, der ebenfalls 6 . ist. 6 x 6 = 36.
6. Berechnen Sie die Quadratwurzel. 36 ist ein perfektes Quadrat und √36 = 6. Vergessen Sie nicht die Einheit, mit der Sie angefangen haben – Zentimeter. Drücken Sie die endgültige Antwort in Quadratzentimetern aus. Die Fläche des Dreiecks mit den Seiten 3, 4 und 5 beträgt 6 cm².
Methode 3 von 4: Verwenden einer Seite eines rechteckigen Dreiecks
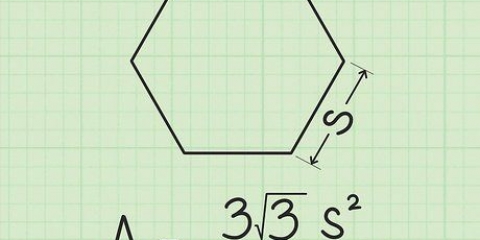
1. Finden Sie die Seite des gleichseitigen Dreiecks. Ein gleichseitiges Dreieck hat gleich lange Seiten und gleiche Winkel. Sie wissen, dass Sie es mit einem gleichseitigen Dreieck zu tun haben, entweder weil dies gegeben ist, oder weil Sie wissen, dass alle Winkel und alle Seiten den gleichen Wert haben. Der Wert einer der Seiten dieses Dreiecks beträgt 6 cm. Beachten Sie dies.
- Wenn Sie wissen, dass Sie es mit einem gleichseitigen Dreieck zu tun haben, aber nur der Umfang bekannt ist, teilen Sie diesen Wert einfach durch 3. Zum Beispiel beträgt die Länge einer Seite eines gleichseitigen Dreiecks mit Umfang 9 ganz einfach 9/3 oder 3.
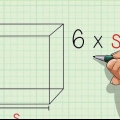
2. Schreiben Sie die Formel auf, um die Fläche eines gleichseitigen Dreiecks zu finden. Die Formel für diese Art von Problem lautet Fläche = (s^2)(√3)/4. Beachten Sie, dass S „Seide“ bedeutet.
3. Wende den Wert einer Seite auf die Gleichung an. Berechnen Sie zuerst das Quadrat der Seite mit dem Wert 6, um 36 . zu erhalten. Bestimme dann den Wert von √3, wenn die Antwort in Dezimalzahlen angegeben werden soll. Geben Sie nun √3 in Ihren Taschenrechner ein, um 1 zu erhalten.732 zu bekommen. Teilen Sie diese Zahl durch 4. Beachten Sie, dass Sie 36 auch durch 4 teilen und dann mit √3 multiplizieren können – die Reihenfolge der Operationen hat keinen Einfluss auf die Antwort.
4. Lösen. Jetzt kommt es hauptsächlich darauf an, nur zu zählen. 36 x 3/4 = 36 x .433 = 15.59 cm Die Fläche eines gleichseitigen Dreiecks mit einer Seitenlänge von 6 cm beträgt 15.59 cm.
Methode 4 von 4: Verwenden der Länge von zwei Seiten und des eingeschlossenen Winkels
1. Bestimmen Sie den Wert der Längen von zwei Seiten und den eingeschlossenen Winkel. Der eingeschlossene Winkel ist der Winkel zwischen den beiden bekannten Seiten des Dreiecks. Sie müssen diese Werte kennen, um mit dieser Methode die Fläche eines Dreiecks zu finden. Nehmen wir ein Dreieck mit folgenden Abmessungen an:
- Winkel A = 123º
- Seite b = 150 cm
- Seite c = 231 cm
2. Schreiben Sie die Formel auf, um die Fläche des Dreiecks zu finden. Die Formel zum Ermitteln der Fläche eines Dreiecks mit zwei bekannten Seiten und einem bekannten eingeschlossenen Winkel lautet wie folgt: Fläche = 1/2(b)(c) x sin A. In dieser Gleichung repräsentieren "B" und "C" die Längen der Seiten und "ein" die Ecke. Sie sollten in dieser Gleichung immer den Sinus des Winkels nehmen.
3. Tragen Sie die Werte in die Gleichung ein. So sieht die Gleichung aus, nachdem Sie diese Werte eingegeben haben:
4. Lösen. Um diese Gleichung zu lösen, multipliziere zuerst die Seiten und dividiere das Ergebnis durch zwei. Dann multiplizieren Sie dieses Ergebnis mit dem Sinus des Winkels. Den Wert des Sinus finden Sie mit Ihrem Taschenrechner. Vergiss nicht, deine Antwort in Kubikeinheiten anzugeben. So geht`s:
Tipps
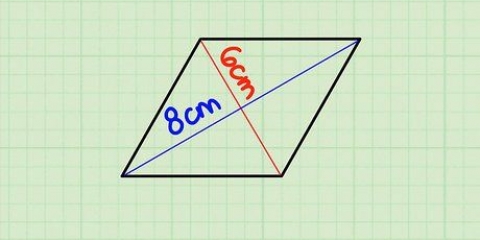
- Wenn Sie nicht verstehen, warum die Grundformel - Körpergröße so funktioniert, finden Sie hier eine kurze Erklärung. Wenn Sie ein zweites, identisches Dreieck erstellen und nebeneinander legen, entsteht entweder ein Rechteck (zwei rechtwinklige Dreiecke) oder ein Parallelogramm (zwei nicht rechtwinklige Dreiecke). Um die Fläche eines Rechtecks oder Parallelogramms zu finden, musst du nur die Basis mit der Höhe multiplizieren. Da ein Dreieck gleich einem halben Rechteck oder Parallelogramm ist, folgt daraus, dass die Fläche eines Dreiecks gleich einer halben Basis mal seiner Höhe ist.
"Berechnen sie die fläche eines dreiecks"
Оцените, пожалуйста статью
