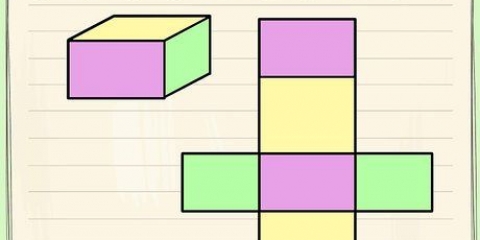
Beachten Sie, dass die einzelnen Striche an den breiten Seiten des Rechtecks bedeuten, dass die beiden Breiten gleich lang sind. 

ein = 4cm * 5cm ein = 20 cm² 
Sie können Ihre endgültige Antwort auf zwei Arten schreiben: 20 Quadratzentimeter oder 20 cm². 

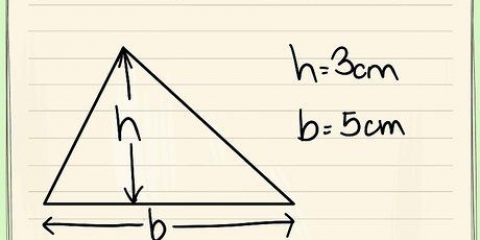
Z.B.:6²+ b² = 10² 36 + b² = 100 b² = 100 - 36 b² = 64 Quadratwurzel (b) = Quadratwurzel (64) b = 8 Die Länge der anderen Seite des Dreiecks, die auch die andere Seite des Rechtecks ist, beträgt 8 cm. 
Z.B.:6cm * 8cm = 48cm² 
Berechnen sie die fläche eines rechtecks
Ein Rechteck ist ein Viereck mit zwei gleich langen und zwei gleich breiten Seiten, das vier rechte Winkel enthält.Um die Fläche eines Rechtecks zu ermitteln, multiplizieren Sie einfach die Länge mit der Breite.Wenn Sie wissen möchten, wie Sie die Fläche eines Rechtecks finden, folgen Sie einfach diesen einfachen Schritten.
Schritte
Methode 1 von 3: Die Grundlagen eines Rechtecks verstehen

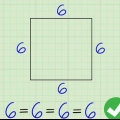
1. Verstehe das Rechteck.Das Rechteck ist ein Viereck, d.h. es hat vier Seiten.Seine gegenüberliegenden Seiten sind gleich lang, also sind die Seiten entlang seiner Länge gleich und die Seiten entlang seiner Breite sind auch gleich.Wenn beispielsweise eine Seite des Rechtecks 10 ist, dann ist die gegenüberliegende Seite auch 10.
- Ebenso ist jedes Quadrat ein Rechteck, aber nicht alle Rechtecke sind Quadrate.Behandeln Sie Quadrate also als Rechtecke, wenn Sie ihre Fläche ermitteln.

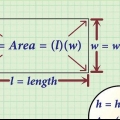
2. Lernen Sie die Gleichung zum Bestimmen der Fläche eines Rechtecks.Die Gleichung zum Bestimmen der Fläche eines Rechtecks lautet einfach ein = l * B.Dies bedeutet, dass die Fläche gleich der Länge des Rechtecks mal seiner Breite ist.
Methode 2 von 3: Finden der Fläche eines Rechtecks

1. Finden Sie die Länge des Rechtecks.In den meisten Fällen erhalten Sie die Länge, aber wenn nicht, können Sie sie mit einem Lineal ermitteln.
- Beachten Sie, dass die doppelten Striche an den langen Seiten des Rechtecks bedeuten, dass die Längen der beiden Seiten gleich sind .

2. Finden Sie die Breite des Rechtecks.Verwenden Sie die gleichen Methoden, um es zu finden.

3. Schreiben Sie die Länge und Breite nebeneinander.In diesem Beispiel beträgt die Länge 5 cm und die Breite 4 cm.

4. Multiplizieren Sie die Länge mit der Breite.Ihre Höhe beträgt 5 cm und Ihre Breite beträgt 4 cm, also müssen Sie sie in die Gleichung einsetzen ein = l * B Orte, um die Oberfläche zu finden.

5. Bitte geben Sie Ihre Antwort in Quadrateinheiten an.Ihre endgültige Antwort ist 20 cm², was bedeutet zwanzig Zentimeter im Quadrat.
Methode 3 von 3: Den Bereich ermitteln, wenn Sie nur die Länge einer Seite und die Diagonale kennen

1. Den Satz des Pythagoras verstehen.Der Satz des Pythagoras ist eine Formel zum Bestimmen der dritten Seite eines rechtwinkligen Dreiecks, wenn Sie den Wert von zwei seiner Seiten kennen.Sie können dies verwenden, um die Hypotenuse des Dreiecks zu finden, die die längste Seite des Dreiecks ist oder deren Länge oder Breite im rechten Winkel zusammentrifft.
- Da ein Rechteck aus vier rechten Winkeln besteht, bildet die Diagonale, die die Form durchschneidet, ein rechtwinkliges Dreieck, sodass Sie den Satz des Pythagoras anwenden können.
- Der Satz lautet: a² + b² = c², wobei a und b Seiten des Dreiecks und c die Hypotenuse oder längste Seite des Dreiecks sind.

2. Verwenden Sie den Satz des Pythagoras, um nach der anderen Seite des Dreiecks aufzulösen.Angenommen, Sie haben ein Rechteck mit einer Seitenlänge von 6 cm und einer Diagonale von 10 cm.Verwenden Sie die 6 cm als eine Seite, verwenden Sie b für die andere Seite und verwenden Sie die 10 cm als Ihre Hypotenuse.Setzen Sie nun einfach Ihre bekannten Größen in den Satz des Pythagoras ein und lösen Sie.So geht`s:

3. Multiplizieren Sie die Länge mit der Breite.Nachdem Sie nun den Satz des Pythagoras verwendet haben, um die Länge und Breite des Rechtecks zu bestimmen, müssen Sie sie nur noch multiplizieren.

4. Bitte geben Sie Ihre Antwort in Quadrateinheiten an.Ihre endgültige Antwort lautet 48 cm² oder 48 Quadratzentimeter.
Tipps
- Alle Quadrate sind Rechtecke, aber nicht alle Rechtecke sind Quadrate.
- Wenn Sie nach einem Gebiet suchen, wird Ihre Antwort immer quadratisch sein.
"Berechnen sie die fläche eines rechtecks"
Оцените, пожалуйста статью