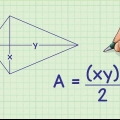
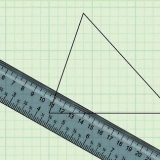
Die beiden kürzeren Seiten des Dreiecks sind die Seiten des Quadrats: jede hat eine Länge S. Die Hypotenuse ist die Diagonale des Quadrats, D. 


Vereinfachen: 
Teilen Sie beide Seiten durch zwei: 
Fläche = 
Fläche = 

Angenommen, ein Quadrat hat eine Diagonale von 10 cm. Fläche = 
=
= 50 cm². Zum Beispiel hat ein Quadrat mit einer Diagonale von 10 cm Seitenlängen  cm.
cm. Wenn Sie sowohl die Länge einer Seite als auch die Fläche der Diagonale ermitteln möchten, können Sie zuerst diese Formel verwenden und dann die Antwort für die Fläche quadrieren: Fläche  cm. Dies ist etwas weniger genau, weil
cm. Dies ist etwas weniger genau, weil  ist eine irrationale Zahl, die Rundungsfehler aufweisen kann.
ist eine irrationale Zahl, die Rundungsfehler aufweisen kann. Zeichne ein Quadrat auf Papier. Stellen Sie sicher, dass alle Seiten gleich sind. Messen Sie die Diagonale. Zeichne ein zweites Quadrat mit dieser Länge als Seiten des Quadrats. Zeichne eine Kopie deines ersten Quadrats, sodass du zwei hast. Schneide alle drei Quadrate aus. Schneiden Sie die beiden kleineren Quadrate in Formen, die in das große Quadrat passen. Sie müssen den Raum perfekt ausfüllen, um zu zeigen, dass die Fläche des großen Quadrats genau doppelt so groß ist wie die des kleineren Quadrats.
Berechnen der fläche eines quadrats mit der diagonalen
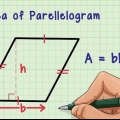
Die gebräuchlichste Formel für die Fläche eines Quadrats ist einfach: Es ist die Länge einer seiner Seiten im Quadrat oder s. Aber manchmal kennt man nur die Länge der Diagonale eines Quadrats, der Linie zwischen zwei gegenüberliegenden Eckpunkten. Wenn Sie mit rechtwinkligen Dreiecken vertraut sind, können Sie eine neue Formel mit der Diagonale als einzige Variable herleiten.
Schritte
Teil 1 von 2: Berechnen der Fläche eines Quadrats

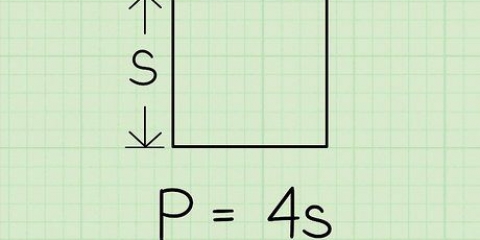
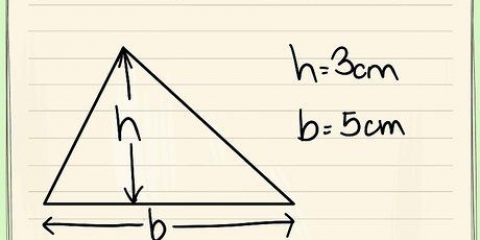
1. Zeichne dein Quadrat. Ein Quadrat hat vier gleiche Seiten. Nehmen wir an, jede Seite hat eine Länge von `s`.

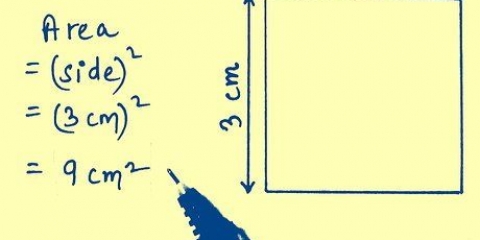
2. Verwenden Sie die Standardformel für die Fläche eines Quadrats. Die Fläche eines Quadrats ist gleich seiner Länge mal seiner Breite. Denn jede Seite S wird Formel Fläche = s x s = s. Das wird sich bald als nützlich erweisen.

3. Verbinden Sie zwei gegenüberliegende Ecken zu einer Diagonale. Das Maß dieser Diagonale wird D Einheiten. Diese Diagonale teilt das Quadrat in zwei rechtwinklige Dreiecke.

4.Verwenden Sie den Satz des Pythagoras für eines der Dreiecke. Der Satz des Pythagoras ist eine Formel zum Bestimmen der Hypotenuse (längste Seite) eines rechtwinkligen Dreiecks: (Seite A) + (Seite B) = (Hypotenuse) oder  . Nachdem das Quadrat in zwei Hälften geteilt wurde, können Sie diese Formel auf eines der rechtwinkligen Dreiecke anwenden:
. Nachdem das Quadrat in zwei Hälften geteilt wurde, können Sie diese Formel auf eines der rechtwinkligen Dreiecke anwenden:
 . Nachdem das Quadrat in zwei Hälften geteilt wurde, können Sie diese Formel auf eines der rechtwinkligen Dreiecke anwenden:
. Nachdem das Quadrat in zwei Hälften geteilt wurde, können Sie diese Formel auf eines der rechtwinkligen Dreiecke anwenden:

5. Ordne die Gleichung so an, dass s auf einer Seite liegt. Denken Sie daran, dass wir wissen, dass die Fläche des Quadrats s ist. Wenn Sie s auf einer Seite isolieren können, haben Sie eine neue Gleichung für die Fläche:






6. Verwenden Sie diese Formel mit einem Beispielquadrat. Diese Schritte haben bewiesen, dass die Formel Fläche =  gilt für alle Quadrate. Geben Sie die Länge der Diagonale für ein D und lösen.
gilt für alle Quadrate. Geben Sie die Länge der Diagonale für ein D und lösen.
 gilt für alle Quadrate. Geben Sie die Länge der Diagonale für ein D und lösen.
gilt für alle Quadrate. Geben Sie die Länge der Diagonale für ein D und lösen.
=

= 50 cm².
Teil2 von 2: Zusätzliche Informationen
1. Finden Sie die Diagonale der Länge einer Seite. Der Satz des Pythagoras für ein Quadrat mit Seite S und diagonal D gib dir die formel  an. Lösen Sie nach `d` auf, wenn Sie die Längen der Seiten kennen und die Länge der Diagonale bestimmen möchten:
an. Lösen Sie nach `d` auf, wenn Sie die Längen der Seiten kennen und die Länge der Diagonale bestimmen möchten:
 an. Lösen Sie nach `d` auf, wenn Sie die Längen der Seiten kennen und die Länge der Diagonale bestimmen möchten:
an. Lösen Sie nach `d` auf, wenn Sie die Längen der Seiten kennen und die Länge der Diagonale bestimmen möchten: - Wenn ein Quadrat beispielsweise eine Seitenlänge von 7 cm hat, beträgt die Diagonale d = 7√2 cm oder etwa 9,9 cm.
- Wenn Sie keinen Taschenrechner haben, können Sie 1,4 als Schätzung von √2 . verwenden.
2. Bestimmen Sie die Länge einer Seite mit der Diagonale. Ist die Diagonale gegeben und Sie wissen, dass die Diagonale eines Quadrats  dann kannst du beide seiten teilen durch
dann kannst du beide seiten teilen durch  zu
zu  bekommen.
bekommen.
 dann kannst du beide seiten teilen durch
dann kannst du beide seiten teilen durch  zu
zu  bekommen.
bekommen. cm.
cm. cm. Dies ist etwas weniger genau, weil
cm. Dies ist etwas weniger genau, weil  ist eine irrationale Zahl, die Rundungsfehler aufweisen kann.
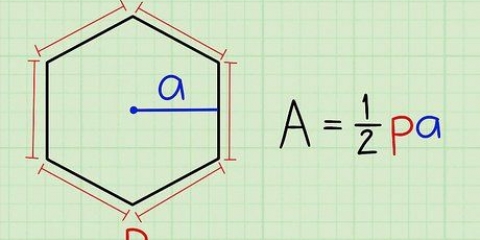
ist eine irrationale Zahl, die Rundungsfehler aufweisen kann.3. Interpretieren Sie die Oberflächenformel. Die Formel Fläche =  scheint mathematisch korrekt zu sein, aber gibt es eine Möglichkeit, dies direkt zu testen?? Brunnen,
scheint mathematisch korrekt zu sein, aber gibt es eine Möglichkeit, dies direkt zu testen?? Brunnen,  ist die Fläche eines zweiten Quadrats mit der Diagonale als Seite. Denn die vollständige Formel
ist die Fläche eines zweiten Quadrats mit der Diagonale als Seite. Denn die vollständige Formel  Sie können folgern, dass dieses zweite Quadrat genau die doppelte Fläche des ursprünglichen Quadrats hat. Das können Sie selbst testen:
Sie können folgern, dass dieses zweite Quadrat genau die doppelte Fläche des ursprünglichen Quadrats hat. Das können Sie selbst testen:
 scheint mathematisch korrekt zu sein, aber gibt es eine Möglichkeit, dies direkt zu testen?? Brunnen,
scheint mathematisch korrekt zu sein, aber gibt es eine Möglichkeit, dies direkt zu testen?? Brunnen,  ist die Fläche eines zweiten Quadrats mit der Diagonale als Seite. Denn die vollständige Formel
ist die Fläche eines zweiten Quadrats mit der Diagonale als Seite. Denn die vollständige Formel  Sie können folgern, dass dieses zweite Quadrat genau die doppelte Fläche des ursprünglichen Quadrats hat. Das können Sie selbst testen:
Sie können folgern, dass dieses zweite Quadrat genau die doppelte Fläche des ursprünglichen Quadrats hat. Das können Sie selbst testen:Tipps
- Diese einfache Gleichung wird in vielen Bereichen verwendet, einschließlich Kristallographie, Chemie und Kunst. Sie können damit beispielsweise die Fläche einer Landschaft berechnen, die Sie beim Vermessen sehen, oder wenn Sie die Perspektive in der Fotografie oder Malerei verwenden, indem Sie die zurückgelegte Entfernung messen und sich ein Raster dieser Entfernung als Diagonale vorstellen.
- Wenn Sie einen visuelleren Ansatz für die Mathematik verfolgen oder lernen möchten, wie Sie Grafiken und Diagramme in der Kunst verwenden oder den spiralförmigen Pfad eines Partikels erkunden möchten, lesen Sie einige Artikel zu Microsoft Excel, Mathematik, Tabellenkalkulationen und Grafiken.
- Wenn Sie keinen Taschenrechner haben, aber eine genauere Schätzung der Quadratwurzel von zwei benötigen, gibt es Möglichkeiten: um dies von Hand zu tun. Ein Beispiel hierfür ist die Newton-Raphson-Methode.
"Berechnen der fläche eines quadrats mit der diagonalen"
Оцените, пожалуйста статью