Berechnung der diagonalen eines quadrats

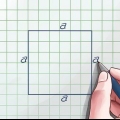
Die Diagonale eines Quadrats ist die Linie von einer Ecke dieses Quadrats zur gegenüberliegenden Ecke. Um die Diagonale eines Quadrats zu bestimmen, verwenden Sie die Formel D=S2{displaystyle d=s{sqrt {2}}}d=s{sqrt{2}}, wodurch S{displaystyle s}S ist gleich der Länge einer Seite des Quadrats. Sum wird jedoch nach der Länge der Diagonale gefragt, was einen anderen Wert ergibt, z. B. den Umfang oder die Fläche des Quadrats. In diesen Fällen ist es notwendig, zuerst verschiedene Formeln zu verwenden, um die Länge der Seite zu bestimmen, bevor Sie die Formel für die Diagonale verwenden.

Schritte

Methode 1 von 3: Wenn Sie die Länge einer Seite kennen

Bild mit dem Titel Berechnen Sie eine Diagonale eines Quadrats Schritt 1
1. Finden Sie die Länge einer Seite des Quadrats. Das ist wohl gegeben. Wenn Sie es in der realen Welt mit einem Quadrat zu tun haben, verwenden Sie ein Lineal oder ein Maßband, um seine Länge zu bestimmen. Da alle vier Seiten des Quadrats gleich lang sind, können Sie jede Seite des Quadrats verwenden. Wenn Sie die Seiten des Quadrats nicht kennen, können Sie diese Methode nicht verwenden.
  • Finden Sie zum Beispiel die Länge der Diagonale eines Quadrats mit einer Seitenlänge von 5 cm.
Bild mit dem Titel Berechnen Sie eine Diagonale eines Quadrats Schritt 2
2. Schreiben Sie die Formel auf:D=S2{displaystyle d=s{sqrt {2}}}d=s{sqrt{2}}. In der Formel ist D{displaystyle d}D gleich der Länge der Diagonale und S{displaystyle s}S gleich einer Seite des Quadrats.
  • Diese Formel leitet sich aus dem Satz des Pythagoras ab (ein2+B2=C2){displaystyle a^{2}+b^{2}=c^{2})}a^{2}+b^{2}=c^{2}). Eine Diagonale teilt ein Quadrat in zwei kongruente rechtwinklige Dreiecke, sodass Sie die Länge der Seiten des Quadrats verwenden können, um die Länge der Diagonale (die Hypotenuse des rechtwinkligen Dreiecks) zu bestimmen.
    • Bild mit dem Titel Berechnen Sie eine Diagonale eines Quadrats Schritt 3
    3. Geben Sie die Seitenlänge des Quadrats in die Formel ein. Stellen Sie sicher, dass Sie die Variable ersetzen S{displaystyle s}S.
  • Wenn die Seiten des Quadrats beispielsweise eine Länge von jeweils 5 Zentimetern haben, würde die Formel so aussehen:
    D=52{displaystyle d=5{sqrt {2}}}d=5{sqrt{2}}
    • Bild mit dem Titel Berechnen Sie eine Diagonale eines Quadrats Schritt 4
    4. Multiplizieren Sie die Länge der Seite mit 2{displaystyle {sqrt {2}}}{sqrt{2}}. Daraus ergibt sich die Länge der Diagonalen. Diese Berechnung erfolgt am besten mit einem Taschenrechner, damit die Antwort genauer ist. Hab keinen Taschenrechner, runde 2{displaystyle {sqrt {2}}}{sqrt{2}} dann ab auf 1.414.
  • Wenn Sie beispielsweise die Diagonale eines 5-Zentimeter-Quadrats berechnen, sieht Ihre Formel so aus:
    D=52{displaystyle d=5{sqrt {2}}}d=5{sqrt{2}}
    D=7.07{displaystyle d=7.07}d=7,07
    Die Diagonale des Quadrats ist also 7,07 Zentimeter lang.

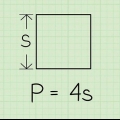
    • Methode 2 von 3: Wenn der Umfang angegeben ist

    Bild mit dem Titel Berechnen Sie eine Diagonale eines Quadrats Schritt 5
    1. Schreiben Sie die Formel für den Umfang eines Quadrats. Die Formel lautet P=4S{displaystyle P=4s}P=4s, wodurch P{displaystyle P}P gleich dem Umfang des Quadrats ist und S{displaystyle s}S gleich der Länge einer Seite des Quadrats.
    • Diese Methode funktioniert nur, wenn der Umfang des Quadrats angegeben ist.
    • Um die Länge der Diagonale zu ermitteln, müssen Sie zuerst die Länge einer Seite des Quadrats ermitteln, also müssen Sie die Formel für den Umfang verwenden und S{displaystyle s}S lösen.
    Bild mit dem Titel Berechnen Sie eine Diagonale eines Quadrats Schritt 6
    2. Setze die Länge des Umfangs in die Formel ein. Stellen Sie sicher, dass Sie die Variable ausfüllen P{displaystyle P}P.
  • Wenn der Umfang des Quadrats beispielsweise 20 Zentimeter beträgt, würde Ihre Formel wie folgt aussehen:
    20=4S{displaystyle 20=4s}20=4s
    • Bild mit dem Titel Berechnen Sie eine Diagonale eines Quadrats Schritt 7
    3. Lösen für S{displaystyle s}S. Teilen Sie dazu jede Seite der Gleichung durch 4. Dadurch erhalten Sie die Länge einer Seite des Quadrats.
  • Zum Beispiel:
    20=4S{displaystyle 20=4s}20=4s
    204=4S4{displaystyle {frac {20}{4}}={frac {4s}{4}}}{frac{20}{4}}={frac{4s}{4}}
    5=S{displaystyle 5=s}5=s
    • Bild mit dem Titel Berechnen Sie eine Diagonale eines Quadrats Schritt 8
    4. Schreiben Sie die Formel D=S2{displaystyle d=s{sqrt {2}}}d=s{sqrt{2}}. In der Formel ist D{displaystyle d}D gleich der Länge der Diagonale und S{displaystyle s}S gleich einer Seite des Quadrats.
  • Diese Formel leitet sich aus dem Satz des Pythagoras ab (ein2+B2=C2){displaystyle a^{2}+b^{2}=c^{2})}a^{2}+b^{2}=c^{2}). Eine Diagonale teilt ein Quadrat in zwei kongruente rechtwinklige Dreiecke, daher können Sie die Länge der Seiten des Quadrats verwenden, um die Länge der Diagonale (die Hypotenuse des rechtwinkligen Dreiecks) zu bestimmen.
    • Bild mit dem Titel Berechnen Sie eine Diagonale eines Quadrats Schritt 9
    5. Setze die Seitenlänge des Quadrats in die Formel ein. Stellen Sie sicher, dass Sie die Variable ersetzen S{displaystyle s}S.
  • Wenn das Quadrat beispielsweise eine Länge von 5 Zentimetern hat, würde die Formel so aussehen:
    D=52{displaystyle d=5{sqrt {2}}}d=5{sqrt{2}}
    • Bild mit dem Titel Berechnen Sie eine Diagonale eines Quadrats Schritt 10
    6. Multiplizieren Sie die Länge der Seite mit 2{displaystyle {sqrt {2}}}{sqrt{2}}. Dadurch erhältst du die Länge der Diagonale. Führen Sie diese Berechnung am besten mit einem Taschenrechner durch, um ein genaueres Ergebnis zu erhalten. Wenn du keinen Taschenrechner hast, runde auf 2{displaystyle {sqrt {2}}}{sqrt{2}} aus bei 1,414.
  • Wenn Sie beispielsweise die Diagonale eines 5-Zentimeter-Quadrats berechnen, würde Ihre Formel so aussehen:
    D=52{displaystyle d=5{sqrt {2}}}d=5{sqrt{2}}
    D=7,07{displaystyle d=7.07}d=7,07
    Die Diagonale des Quadrats ist also 7,07 Zentimeter lang.

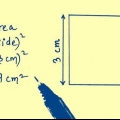
    • Methode 3 von 3: Wenn die Fläche angegeben ist

    Bild mit dem Titel Berechnen Sie eine Diagonale eines Quadrats Schritt 11
    1. Schreiben Sie die Formel für die Fläche eines Quadrats. Die Formel lautet ein=S2{displaystyle A=s^{2}}A=s^{{2}}, wodurch ein{displaystyle A}ein gleich der Fläche des Quadrats ist, und S{displaystyle s}S gleich der Länge einer Seite des Quadrats.
    • Diese Methode funktioniert nur, wenn die Fläche des Quadrats bekannt ist.
    • Um die Länge der Diagonale zu ermitteln, müssen Sie zuerst die Länge einer Seite des Quadrats bestimmen, den Grund, warum Sie zuerst die Flächenformel verwenden müssen, und S{displaystyle s}S lösen.
    Bild mit dem Titel Berechnen Sie eine Diagonale eines Quadrats Schritt 12
    2. Ersetzen Sie den Wert für die Fläche in der Formel. Stellen Sie sicher, dass Sie die Variable ersetzen ein{displaystyle A}ein.
  • Wenn die Fläche des Quadrats beispielsweise 25 Quadratzentimeter beträgt, würde Ihre Formel so aussehen:
    25=S2{displaystyle 25=s^{2}}25=s^{{2}}
    • Bild mit dem Titel Berechnen Sie eine Diagonale eines Quadrats Schritt 13
    3. Lösen für S{displaystyle s}S. Sie tun dies, indem Sie die Quadratwurzel der Fläche bestimmen. Dies gibt Ihnen die Länge einer Seite des Quadrats. Bestimme nun die Quadratwurzel mit einem Taschenrechner. Wenn Sie Hilfe bei der Berechnung der Quadratwurzel von Hand benötigen, lesen Sie Berechnen Sie die Quadratwurzel einer Zahl ohne Taschenrechner.
  • Zum Beispiel:
    25=S2{displaystyle 25=s^{2}}25=s^{{2}}
    25=S2{displaystyle {sqrt {25}}={sqrt {s^{2}}}}{sqrt{25}}={sqrt{s^{{2}}}}
    5=S{displaystyle 5=s}5=s
    • Bild mit dem Titel Berechnen Sie eine Diagonale eines Quadrats Schritt 14
    4. Schreiben Sie die Formel D=S2{displaystyle d=s{sqrt {2}}}d=s{sqrt{2}}. In der Formel ist D{displaystyle d}D gleich der Länge der Diagonale und ist S{displaystyle s}S gleich einer Seite des Quadrats.
  • Diese Formel leitet sich aus dem Satz des Pythagoras ab (ein2+B2=C2){displaystyle a^{2}+b^{2}=c^{2})}a^{2}+b^{2}=c^{2}). Eine Diagonale teilt ein Quadrat in zwei kongruente rechtwinklige Dreiecke, sodass Sie die Länge der Seiten des Quadrats verwenden können, um die Länge der Diagonale (die Hypotenuse des rechtwinkligen Dreiecks) zu bestimmen.
    • Bild mit dem Titel Berechnen Sie eine Diagonale eines Quadrats Schritt 15
    5. Verwenden Sie die Länge der Seite des Quadrats in der Formel. Stellen Sie sicher, dass Sie die Variable ersetzen S{displaystyle s}S.
  • Wenn das Quadrat beispielsweise eine Länge von 5 Zentimetern hat, würde die Formel so aussehen:
    D=52{displaystyle d=5{sqrt {2}}}d=5{sqrt{2}}
    • Bild mit dem Titel Berechnen Sie eine Diagonale eines Quadrats Schritt 16
    6. Multiplizieren Sie die Länge der Seite mit 2{displaystyle {sqrt {2}}}{sqrt{2}}. Dadurch erhältst du die Länge der Diagonale. Führen Sie diese Berechnung am besten mit einem Taschenrechner durch, um ein genaueres Ergebnis zu erhalten. Wenn du keinen Taschenrechner hast, runde auf 2{displaystyle {sqrt {2}}}{sqrt{2}} aus bei 1,414.
  • Wenn Sie beispielsweise die Diagonale eines 5-Zentimeter-Quadrats berechnen, würde Ihre Formel so aussehen:
    D=52{displaystyle d=5{sqrt {2}}}d=5{sqrt{2}}
    D=7,07{displaystyle d=7.07}d=7,07
    Die Diagonale des Quadrats beträgt also 7,07 Zentimeter.

    • Notwendigkeiten

    • Taschenrechner

    De.FaqCartx.info / Bildung & kommunikation
    Оцените, пожалуйста статью
    Verwendung von microsoft word
    Verwendung von microsoft word
    Mach weniger klebrigen schleim
    Mach weniger klebrigen schleim
    Den unterschied zwischen einem wahren und einem falschen liebhaber ...
    Den unterschied zwischen einem wahren und einem falschen liebhaber ...
    Stärken sie ihre zähne und ihr zahnfleisch
    Stärken sie ihre zähne und ihr zahnfleisch
    Anbau von chilischoten
    Anbau von chilischoten
    Über deinen ex hinwegkommen, der dich entjungfert hat
    Über deinen ex hinwegkommen, der dich entjungfert hat