Sie arbeiten jetzt an einem gleichseitigen Dreieck, da alle drei Seiten der Figur genau gleich lang sind. Aber denken Sie daran, dass diese Formel für alle Dreiecke gilt. 
Ein weiteres Beispiel: Wenn a = 4, b = 3, und c=5, dann ist der Umfang 3 + 4 + 5, mit anderen Worten 12. 
In diesem Beispiel sind die Seiten alle 5 cm groß, die richtige Antwort ist also 15 cm. 



Wenn Sie zum Beispiel wissen, dass Seide a = 3 und Seide b = 4, schreibe es dann in die Formel wie folgt: 3 + 4 = c. Ein zweites Beispiel: Wenn Sie wissen, dass die Seitenlängea = 6, und die hypotenuse c = 10, dann setzt du es so in die Gleichung ein: 6 + b = 10. 
Im ersten Beispiel multiplizieren Sie die Werte in 3 + 4 = c und du entdeckst das und 25= c. Berechnen Sie dann die Quadratwurzel von 25, so dass Sie zu . kommen c = 25. Im zweiten Beispiel multiplizieren Sie die Werte in 6 + b = 10 und du entdeckst das 36 + b = 100.Subtrahiere 36 von 100, um zu erhalten b = 64, und berechne dann die Quadratwurzel von 64, sodass du erhältst b = 8. 
Im ersten Beispiel ist das X = 3 + 4 + 5 oder 12. Im zweiten Beispiel ist das X = 6 + 8 + 10 oder 24. 

Stellen Sie sich zum Beispiel ein Dreieck mit einer Seite von 10 und einer von 12 vor, und einem Winkel von 97° dazwischen. Dann schreiben wir die Variablen wie folgt:a = 10, b = 12, C = 97°. 
c = 10 + 12 - 2 × 10 × 12 × weil(97). c = 100 + 144 – (240 × -0,12187)(Runde den Kosinus auf 5 Stellen nach dem Komma) c = 244 – (-29,25) c = 244 + 29,25(Nehmen Sie das Minuszeichen, wenn weil(C) ist negativ!) c = 273,25 c = 16,53 
In unserem Beispiel: 10 + 12 + 16,53 = 38,53, das ist der Umfang unseres Dreiecks!
Berechnung des umfangs eines dreiecks
Der Umfang eines Dreiecks ist die Länge einer Linie, die entlang der Seiten des Dreiecks gezogen werden kann. Am einfachsten ist es, die Längen aller Seiten zu addieren, aber wenn Sie nicht alle Längen kennen, müssen Sie sie zuerst berechnen. In diesem Artikel erfahren Sie zunächst, wie Sie den Umfang eines Dreiecks berechnen, wenn Sie die Längen aller drei Seiten kennen; Dies ist die einfachste und am häufigsten verwendete Methode. Dann lernst du den Umfang zu berechnen, wenn du nur die Längen von zwei der drei Seiten kennst. Schließlich wird erklärt, wie man den Umfang berechnet, wenn man die Längen zweier Seiten und den Winkel zwischen ihnen kennt, unter Verwendung des Kosinusgesetzes.
Schritte
Methode 1 von 3: Berechnung des Umfangs eines Dreiecks, wenn die Längen aller Seiten gegeben sind

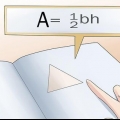
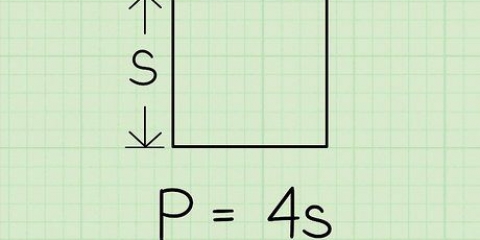
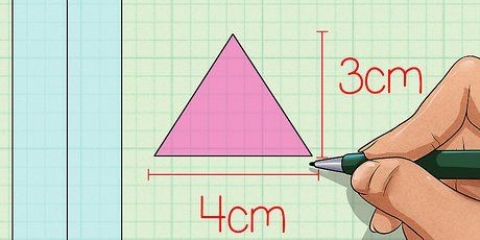
1. Lernen Sie die Formel zum Ermitteln des Umfangs. Die Formel lautet: A + B + C = X wodurch ein, B, und C repräsentieren die Längen der Seiten und x der Umfang.
- Diese Formel bedeutet im Grunde, dass Sie zum Ermitteln des Umfangs eines Dreiecks die Längen der drei Seiten addieren müssen.

2. Bestimme die Längen aller drei Seiten. In diesem Beispiel: ein = 5, B = 5, C = 5.

3. Addiere die Längen der drei Seiten zusammen. In diesem Beispiel: 5 + 5 + 5 = 15. Der Umfang des Dreiecks (X) ist also fünfzehn.

4. Denken Sie daran, immer die Einheiten in Ihre Antwort aufzunehmen. Wenn die Seiten in Zentimetern angegeben sind, muss Ihre endgültige Antwort auch in Zentimetern angegeben werden. Wenn die Seiten in Bezug auf eine Variable angegeben sind, zum Beispiel x, dann muss die Antwort auch in Bezug auf x . sein.
Methode 2 von 3: Berechnung des Umfangs, wenn nur zwei Seiten des Dreiecks gegeben sind

1. Wissen, was ein rechtwinkliges Dreieck ist. Ein rechtwinkliges Dreieck ist ein Dreieck mit einem rechten Winkel (90 Grad). Die diesem rechten Winkel gegenüberliegende Seite des Dreiecks ist immer die längste Seite, die Hypotenuse oder Hypotenuse genannt wird. Rechtwinklige Dreiecke tauchen regelmäßig in Mathetests auf, aber zum Glück gibt es eine sehr praktische Formel, um die Länge einer unbekannten Seite zu berechnen!

2. Kenne den Satz des Pythagoras. Der Satz des Pythagoras gilt für jedes rechtwinklige Dreieck und lautet: a² + b² = c².

3. Schau dir dein Dreieck an und schreibe an den Seiten ein, B und C. Denken Sie daran, dass die längste Seite Hypotenuse genannt wird. Es befindet sich gegenüber dem rechten Winkel, und Sie müssen auf diese Seite gehen C schreiben. An den beiden kürzeren Seiten schreibst du ein und B. Es spielt keine Rolle, welches Sie wo platzieren, das Ergebnis wird das gleiche sein!

4. Nehmen Sie die Längen der Seiten im Satz des Pythagoras. Erinnere dich daran a + b = c. Tragen Sie die Längen anstelle der entsprechenden Buchstaben ein.

5. Löse die Gleichung, um die fehlende Länge zu finden. Sie müssen zuerst die bekannten Seiten mit sich selbst multiplizieren (zum Beispiel 3 = 3 * 3 = 9).Wenn Sie nach der Hypotenuse suchen, können Sie dann einfach die beiden Werte zusammenzählen und die Quadratwurzel des Ergebnisses berechnen, um die Länge zu finden. Wenn Ihnen eine andere Seite fehlt, müssen Sie die beiden subtrahieren und dann die Quadratwurzel des Ergebnisses berechnen, um die Länge zu finden.

6. Addieren Sie die Längen der drei Seiten zusammen, um den Umfang zu berechnen. Denken Sie an die Gleichung: X = a + b + c. Jetzt kennen Sie die Längen der Seitenein, B und C wissen, dass Sie sie addieren können, um den Umfang zu erhalten.
Methode 3 von 3: Den Umfang eines Dreiecks mit dem Kosinussatz ermitteln

1. Lernen Sie das Kosinusgesetz. Mit dem Kosinussatz können Sie jedes Dreieck lösen, wenn Sie die Längen zweier Seiten und den Winkel zwischen ihnen kennen. Es funktioniert für jedes Dreieck und es ist eine sehr nützliche Formel. Das Kosinusgesetz besagt, dass für jedes Dreieck mit Seiten ein, B, und C, mit gegenüberliegenden Eckenein, B, und C es gilt folgende Formel:c = a + b - 2ab weil(C).

2. Schau dir dein Dreieck an und setze die Buchstaben auf die verschiedenen Teile. Die erste Seite, von der du weißt, dass du sie musst ein nenne es, und der entgegengesetzte Winkel ist dann ein. Die zweite Seite, von der du weißt, dass du sie musst B ruf die gegenüberliegende ecke an B. Der Winkel, von dem Sie wissen, dass Sie ihn brauchen C nenne es, und die dritte Seite, die du lösen willst, ist dann C.

3. Setze deine Informationen in die Gleichung ein und löse nach Seite c. Sie müssen zuerst a und b mit sich selbst multiplizieren und zusammenzählen. Berechnen Sie dann den Kosinus von C mit weil-Funktion auf Ihrem Taschenrechner oder einem Online-Rechner. Multiplizieren weil(C) von 2ab und subtrahiere das Ergebnis von der Summe von a + b.Die Antwort ist C.Berechne die Quadratwurzel daraus und du kennst die Seitenlänge C.In unserem Beispiel:

4. Verwenden Sie die Länge vonC um den Umfang deines Dreiecks zu berechnen. Denken Sie daran, dass die Formel für den Umfang lautet: X = a + b + c, Sie müssen also nur alle Längen addieren, denn ein und B wussten Sie.Stück Kuchen!
"Berechnung des umfangs eines dreiecks"
Оцените, пожалуйста статью