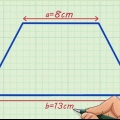
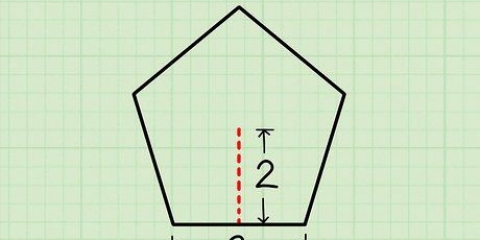
Wenn Sie beispielsweise ein Trapez mit einer Oberseite von 2 cm, einer Unterseite von 3 cm und zwei Seitenlängen von 1 cm haben, würde Ihre Formel so aussehen:


Zum Beispiel:


Der Umfang des Trapezes beträgt also 7 cm. 

Wenn Sie beispielsweise ein Trapez mit einer Höhe von 6 cm haben, müssen Sie von jedem oberen Scheitelpunkt nach unten eine Linie ziehen. Beachten Sie 6 cm für jede Zeile. 
Wenn zum Beispiel die Oberseite des Trapezes 6 cm beträgt, ist der mittlere Teil der Unterseite ebenfalls 6 cm² groß. 

Wenn Sie beispielsweise wissen, dass die Höhe des Trapezes 6 cm beträgt und die Länge der Seite (Hypotenuse) 9 cm beträgt, würde Ihre Gleichung wie folgt aussehen:


Zum Beispiel: ist die Gleichung  , dann quadrieren Sie 6 und 9 und subtrahieren das Quadrat von 6 vom Quadrat von 9:
, dann quadrieren Sie 6 und 9 und subtrahieren das Quadrat von 6 vom Quadrat von 9:




Zum Beispiel:




Also aufpassen als Basis des ersten Dreiecks.
als Basis des ersten Dreiecks. 
Wenn die zweite Seite des Trapezes beispielsweise 7 cm beträgt, berechnen Sie wie folgt:





Also aufpassen als Basis des zweiten Dreiecks.
als Basis des zweiten Dreiecks. 
Zum Beispiel: 
Nachdem Sie die Quadratwurzeln in Dezimalzahlen umgewandelt haben, haben Sie
Der ungefähre Umfang Ihres Trapezes beträgt also 38,314 cm.. 

Wenn Sie beispielsweise ein Trapez mit einer Höhe von 6 cm haben, ziehen Sie eine Linie von jedem oberen Scheitelpunkt nach unten. Beachten Sie 6 cm in jeder Zeile. 
Wenn zum Beispiel die Oberseite des Trapezes 6 cm beträgt, ist der mittlere Teil der Unterseite ebenfalls 6 cm² groß. 
Mit diesem Verhältnis können Sie die Länge der Hypotenuse des Dreiecks ermitteln, die auch die erste Seite des Trapezes ist. Die Hypotenuse ist die Seite gegenüber dem 90-Grad-Winkel eines rechtwinkligen Dreiecks. 
Angenommen, der angegebene Innenwinkel beträgt 35 Grad und die Höhe des Dreiecks beträgt 6 cm, dann sieht Ihre Formel wie folgt aus:


Wenn Sie beispielsweise einen Taschenrechner verwenden, werden Sie feststellen, dass der Sinus eines 35-Grad-Winkels 0,5738 (abgerundet) beträgt. Deine Formel lautet nun also:


Zum Beispiel:




Somit beträgt die Länge der Hypotenuse und der ersten fehlenden Seite des Trapezes etwa 10,4566 cm. 
Wenn der angegebene Innenwinkel beispielsweise 45 Grad beträgt, berechnen Sie:





Die Länge der Hypotenuse und der zweiten fehlenden Seite des Trapezes beträgt also etwa 8,4854 cm. 

Wenn das erste rechtwinklige Dreieck beispielsweise eine Hypotenuse von 10,4566 und eine Höhe von 6 hat, lautet Ihre Formel:


Zum Beispiel:






Die Basis des Dreiecks und der erste fehlende Teil der Unterseite des Trapezes beträgt also etwa 8,5639 cm. 
Wenn das zweite rechtwinklige Dreieck beispielsweise eine Hypotenuse von 8,4854 und eine Höhe von 6 hat, würden Sie wie folgt berechnen:






Die Basis des zweiten Dreiecks und der zweite fehlende Teil des Bodens des Trapezes sind also gleich 6 cm. 
Zum Beispiel: 
Der ungefähre Umfang des Trapezes beträgt also 45,5059 cm.
Berechnung des umfangs eines trapezes
Ein Trapez ist definiert als ein Viereck mit zwei parallelen Seiten. Wie bei jedem Polygon müssen Sie alle vier Seiten zusammenzählen, um den Umfang eines Trapezes (oder Trapezes) zu finden. Oftmals übersehen Sie jedoch Seitenlängen, aber Sie haben andere Daten, wie die Höhe des Trapezes oder die Winkelmaße. Mit diesen Daten können Sie die unbekannten Längen der Seiten nach den Regeln der Geometrie und Trigonometrie ermitteln.
Schritte
Methode 1 von 3: Wenn Sie die Länge beider Seiten und der Basis kennen

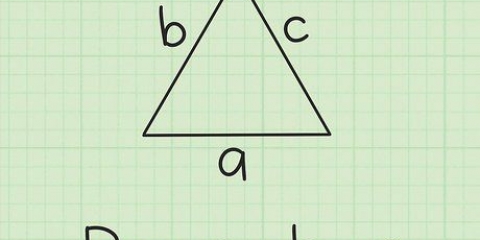
1. Setze die Formel für den Umfang eines Trapezes. Die Formel lautet  , wodurch
, wodurch  gleich dem Umfang des Trapezes ist und die Variable
gleich dem Umfang des Trapezes ist und die Variable  gleich der Länge der Oberseite des Trapezes,
gleich der Länge der Oberseite des Trapezes,  entspricht der Länge des Bodens,
entspricht der Länge des Bodens,  gleich der Länge der linken Seite und
gleich der Länge der linken Seite und  entspricht der Länge der rechten Seite.
entspricht der Länge der rechten Seite.
 , wodurch
, wodurch  gleich dem Umfang des Trapezes ist und die Variable
gleich dem Umfang des Trapezes ist und die Variable  gleich der Länge der Oberseite des Trapezes,
gleich der Länge der Oberseite des Trapezes,  entspricht der Länge des Bodens,
entspricht der Länge des Bodens,  gleich der Länge der linken Seite und
gleich der Länge der linken Seite und  entspricht der Länge der rechten Seite.
entspricht der Länge der rechten Seite.
2. Verwenden Sie die Seitenlängen in der Formel. Wenn Sie die Länge aller vier Seiten des Trapezes nicht kennen, können Sie diese Formel nicht verwenden.


3. Die Seitenlängen zusammenzählen. Dadurch erhalten Sie den Umfang Ihres Trapezes.


Der Umfang des Trapezes beträgt also 7 cm.
Methode 2 von 3: Wenn Sie die Höhe, beide Seitenlängen und die Spitzenlänge kennen

1. Teilen Sie das Trapez in ein Rechteck und zwei rechtwinklige Dreiecke. Zeichnen Sie dazu die Höhe von beiden oberen Ecken.
- Wenn Sie die beiden rechtwinkligen Dreiecke nicht bilden können, weil eine Seite des Trapezes senkrecht zur Grundfläche steht, stellen Sie sicher, dass diese Seite die gleiche Länge wie die Höhe hat, und teilen Sie das Trapez in ein Rechteck und ein rechtwinkliges Dreieck auf.

2. Geben Sie die Länge jeder Konturlinie an. Da dies die gegenüberliegenden Seiten eines Rechtecks sind, haben sie die gleiche Länge.

3. Beachten Sie die Länge des mittleren Teils des Bodens. (Dies ist der untere Rand des Rechtecks.) Die Länge ist gleich der Länge der Oberseite (der Oberseite des Rechtecks), da die gegenüberliegenden Seiten eines Rechtecks die gleiche Länge haben. Wenn Sie die Länge des Oberteils nicht kennen, können Sie diese Methode nicht verwenden.

4. Stellen Sie den Satz des Pythagoras für das erste rechtwinklige Dreieck auf. Die Formel lautet  , wodurch
, wodurch  ist die Länge der Hypotenuse des rechtwinkligen Dreiecks (der Seite gegenüber dem rechten Winkel),
ist die Länge der Hypotenuse des rechtwinkligen Dreiecks (der Seite gegenüber dem rechten Winkel),  ist die Höhe des rechtwinkligen Dreiecks und
ist die Höhe des rechtwinkligen Dreiecks und  ist die Länge der Basis des Dreiecks.
ist die Länge der Basis des Dreiecks.
 , wodurch
, wodurch  ist die Länge der Hypotenuse des rechtwinkligen Dreiecks (der Seite gegenüber dem rechten Winkel),
ist die Länge der Hypotenuse des rechtwinkligen Dreiecks (der Seite gegenüber dem rechten Winkel),  ist die Höhe des rechtwinkligen Dreiecks und
ist die Höhe des rechtwinkligen Dreiecks und  ist die Länge der Basis des Dreiecks.
ist die Länge der Basis des Dreiecks.
5. Verwenden Sie die bekannten Werte des ersten Dreiecks in der Formel. Achten Sie darauf, die Seitenlänge des Trapezes für . einzugeben  . Geben Sie die Höhe des Trapezes für . ein
. Geben Sie die Höhe des Trapezes für . ein  .
.
 . Geben Sie die Höhe des Trapezes für . ein
. Geben Sie die Höhe des Trapezes für . ein  .
.

6. Quadrieren Sie die bekannten Werte in der Gleichung. Ziehen Sie dann die quadrierten Werte voneinander ab, um zu erhalten  isolieren.
isolieren.
 isolieren.
isolieren. , dann quadrieren Sie 6 und 9 und subtrahieren das Quadrat von 6 vom Quadrat von 9:
, dann quadrieren Sie 6 und 9 und subtrahieren das Quadrat von 6 vom Quadrat von 9:



7. Ziehe die Quadratwurzel, um den Wert von zu erhalten B  finden. (Eine vollständige Anleitung zum Vereinfachen von Quadratwurzeln finden Sie unter dieser Artikel zum Thema). Als Ergebnis erhalten Sie den Wert der fehlenden Basis Ihres ersten rechtwinkligen Dreiecks. Schreiben Sie diese Länge an die Basis Ihres Dreiecks.
finden. (Eine vollständige Anleitung zum Vereinfachen von Quadratwurzeln finden Sie unter dieser Artikel zum Thema). Als Ergebnis erhalten Sie den Wert der fehlenden Basis Ihres ersten rechtwinkligen Dreiecks. Schreiben Sie diese Länge an die Basis Ihres Dreiecks.
 finden. (Eine vollständige Anleitung zum Vereinfachen von Quadratwurzeln finden Sie unter dieser Artikel zum Thema). Als Ergebnis erhalten Sie den Wert der fehlenden Basis Ihres ersten rechtwinkligen Dreiecks. Schreiben Sie diese Länge an die Basis Ihres Dreiecks.
finden. (Eine vollständige Anleitung zum Vereinfachen von Quadratwurzeln finden Sie unter dieser Artikel zum Thema). Als Ergebnis erhalten Sie den Wert der fehlenden Basis Ihres ersten rechtwinkligen Dreiecks. Schreiben Sie diese Länge an die Basis Ihres Dreiecks.



Also aufpassen
 als Basis des ersten Dreiecks.
als Basis des ersten Dreiecks.
8. Finden Sie die fehlende Länge des zweiten rechtwinkligen Dreiecks. Stellen Sie dazu den Satz des Pythagoras für das zweite Dreieck auf und folgen Sie den Schritten, um die Länge der fehlenden Seite zu finden. Wenn Sie mit einem gleichschenkligen Trapez arbeiten (dasjenige, bei dem die beiden nicht parallelen Seiten die gleiche Länge haben), dann sind die beiden rechtwinkligen Dreiecke deckungsgleich, sodass der Wert des ersten Dreiecks gleich dem des zweiten Dreiecks ist.





Also aufpassen
 als Basis des zweiten Dreiecks.
als Basis des zweiten Dreiecks.
9. Addiere alle Seitenlängen des Trapezes. Der Umfang eines Polygons ist die Summe aller Seiten:  . Für den Boden füge die Unterseite des Rechtecks plus die Basen der beiden Dreiecke hinzu. Sie werden wahrscheinlich Quadratwurzeln in Ihrer Antwort haben. Eine vollständige Anleitung zum Addieren von Quadratwurzeln finden Sie im Artikel zu diesem Thema. Sie können auch einen Taschenrechner verwenden, um die Quadratwurzeln in Dezimalzahlen umzurechnen.
. Für den Boden füge die Unterseite des Rechtecks plus die Basen der beiden Dreiecke hinzu. Sie werden wahrscheinlich Quadratwurzeln in Ihrer Antwort haben. Eine vollständige Anleitung zum Addieren von Quadratwurzeln finden Sie im Artikel zu diesem Thema. Sie können auch einen Taschenrechner verwenden, um die Quadratwurzeln in Dezimalzahlen umzurechnen.
 . Für den Boden füge die Unterseite des Rechtecks plus die Basen der beiden Dreiecke hinzu. Sie werden wahrscheinlich Quadratwurzeln in Ihrer Antwort haben. Eine vollständige Anleitung zum Addieren von Quadratwurzeln finden Sie im Artikel zu diesem Thema. Sie können auch einen Taschenrechner verwenden, um die Quadratwurzeln in Dezimalzahlen umzurechnen.
. Für den Boden füge die Unterseite des Rechtecks plus die Basen der beiden Dreiecke hinzu. Sie werden wahrscheinlich Quadratwurzeln in Ihrer Antwort haben. Eine vollständige Anleitung zum Addieren von Quadratwurzeln finden Sie im Artikel zu diesem Thema. Sie können auch einen Taschenrechner verwenden, um die Quadratwurzeln in Dezimalzahlen umzurechnen.
Nachdem Sie die Quadratwurzeln in Dezimalzahlen umgewandelt haben, haben Sie

Der ungefähre Umfang Ihres Trapezes beträgt also 38,314 cm..
Methode 3 von 3: Wenn Sie die Höhe, Länge der oberen und unteren Innenecken kennen

1. Teilen Sie das Trapez in ein Rechteck und zwei rechtwinklige Dreiecke. Geben Sie dazu die Höhe von den beiden oberen Ecken an.
- Wenn Sie keine zwei rechtwinkligen Dreiecke bilden können, weil eine Seite des Trapezes senkrecht zur Grundfläche steht, stellen Sie sicher, dass diese Seite die gleiche Größe wie die Höhe hat, und teilen Sie das Trapez in ein Rechteck und ein rechtwinkliges Dreieck auf.

2. Beschriften Sie jede Kontur. Da es sich um gegenüberliegende Seiten eines Rechtecks handelt, haben sie die gleiche Länge.

3. Beachten Sie die Länge des mittleren Teils des Bodens. (Dies ist der untere Rand des Rechtecks.) Diese Länge ist gleich der Länge der Oberseite, da die gegenüberliegenden Seiten eines Rechtecks gleich lang sind.

4. Stellen Sie die Sinusformel für das erste rechtwinklige Dreieck auf. Die Formel lautet  , wodurch
, wodurch  die innere ecke ist,
die innere ecke ist,  die Höhe des Dreiecks und
die Höhe des Dreiecks und  ist die Länge der Hypotenuse.
ist die Länge der Hypotenuse.
 , wodurch
, wodurch  die innere ecke ist,
die innere ecke ist,  die Höhe des Dreiecks und
die Höhe des Dreiecks und  ist die Länge der Hypotenuse.
ist die Länge der Hypotenuse.
5. Verwenden Sie die bekannten Werte im Sinusverhältnis. Achten Sie darauf, die Höhe des Dreiecks als Länge der gegenüberliegenden Seite in der Formel zu verwenden. du löst das für H . auf.


6. Bestimmen Sie den Sinus des Winkels. Tun Sie dies mit der SIN-Taste auf einem wissenschaftlichen Taschenrechner. Verwenden Sie diesen Wert in der Formel.


7. Löse dies für H . auf. Multiplizieren Sie dazu jede Seite mit H und teilen Sie dann jede Seite durch den Sinuswinkel. Oder dividiere die Höhe des Dreiecks durch den Sinuswinkel.




Somit beträgt die Länge der Hypotenuse und der ersten fehlenden Seite des Trapezes etwa 10,4566 cm.

8. Finden Sie die Länge der Hypotenuse des zweiten rechtwinkligen Dreiecks. Stellen Sie die Sinusformel ein ( ) für den zweiten gegebenen Innenwinkel. Dadurch erhältst du die Länge der Hypotenuse, die auch die erste Seite des Trapezes ist.
) für den zweiten gegebenen Innenwinkel. Dadurch erhältst du die Länge der Hypotenuse, die auch die erste Seite des Trapezes ist.
 ) für den zweiten gegebenen Innenwinkel. Dadurch erhältst du die Länge der Hypotenuse, die auch die erste Seite des Trapezes ist.
) für den zweiten gegebenen Innenwinkel. Dadurch erhältst du die Länge der Hypotenuse, die auch die erste Seite des Trapezes ist.




Die Länge der Hypotenuse und der zweiten fehlenden Seite des Trapezes beträgt also etwa 8,4854 cm.

9. Stellen Sie den Satz des Pythagoras für das erste rechtwinklige Dreieck auf. Der Satz des Pythagoras ist laut  , wobei die Länge der Hypotenuse gleich ist
, wobei die Länge der Hypotenuse gleich ist  , und die Höhe des Dreiecks
, und die Höhe des Dreiecks  .
.
 , wobei die Länge der Hypotenuse gleich ist
, wobei die Länge der Hypotenuse gleich ist  , und die Höhe des Dreiecks
, und die Höhe des Dreiecks  .
.
10. Verwenden Sie die bekannten Werte im Satz des Pythagoras für das erste rechtwinklige Dreieck. Stellen Sie sicher, dass Sie den richtigen Wert für die Hypotenuse eingeben  und die Höhe
und die Höhe  .
.
 und die Höhe
und die Höhe  .
.

11. Löse das für B  . Dies gibt Ihnen die Länge der Basis des ersten rechtwinkligen Dreiecks und den ersten fehlenden Teil der Basis des Trapezes.
. Dies gibt Ihnen die Länge der Basis des ersten rechtwinkligen Dreiecks und den ersten fehlenden Teil der Basis des Trapezes.
 . Dies gibt Ihnen die Länge der Basis des ersten rechtwinkligen Dreiecks und den ersten fehlenden Teil der Basis des Trapezes.
. Dies gibt Ihnen die Länge der Basis des ersten rechtwinkligen Dreiecks und den ersten fehlenden Teil der Basis des Trapezes.





Die Basis des Dreiecks und der erste fehlende Teil der Unterseite des Trapezes beträgt also etwa 8,5639 cm.

12. Finden Sie die Länge der fehlenden Basis des zweiten rechtwinkligen Dreiecks. Verwenden Sie den Satz des Pythagoras ( ). Verwenden Sie die Länge der Hypotenuse für
). Verwenden Sie die Länge der Hypotenuse für  und die Höhe für
und die Höhe für  . Löse das für
. Löse das für  und Sie erhalten die Länge des zweiten fehlenden Teils des unteren Trapezes.
und Sie erhalten die Länge des zweiten fehlenden Teils des unteren Trapezes.
 ). Verwenden Sie die Länge der Hypotenuse für
). Verwenden Sie die Länge der Hypotenuse für  und die Höhe für
und die Höhe für  . Löse das für
. Löse das für  und Sie erhalten die Länge des zweiten fehlenden Teils des unteren Trapezes.
und Sie erhalten die Länge des zweiten fehlenden Teils des unteren Trapezes.





Die Basis des zweiten Dreiecks und der zweite fehlende Teil des Bodens des Trapezes sind also gleich 6 cm.

13. Fügen Sie alle Seiten des Trapezes zusammen. Der Umfang eines Polygons ist die Summe aller Seiten:  . Für den unteren Rand füge den unteren Rand des Rechtecks zur Basis der beiden Dreiecke hinzu.
. Für den unteren Rand füge den unteren Rand des Rechtecks zur Basis der beiden Dreiecke hinzu.
 . Für den unteren Rand füge den unteren Rand des Rechtecks zur Basis der beiden Dreiecke hinzu.
. Für den unteren Rand füge den unteren Rand des Rechtecks zur Basis der beiden Dreiecke hinzu.
Der ungefähre Umfang des Trapezes beträgt also 45,5059 cm.
Tipps
- Verwenden Sie die Gesetze spezieller Dreiecke, um die fehlenden Längen spezieller Dreiecke zu finden, ohne die Sinusformel oder den Satz des Pythagoras zu verwenden. Die Gesetze gelten für ein 30-60-90-Dreieck oder ein 90-45-45-Dreieck.
- Verwenden Sie einen wissenschaftlichen Taschenrechner, um den Sinus eines Winkels zu bestimmen, indem Sie den Winkel eingeben und dann die Taste `SIN` drücken. Sie können auch eine Trigonometrietabelle verwenden.
Notwendigkeiten
- Taschenrechner
- Bleistift
- Papier
"Berechnung des umfangs eines trapezes"
Оцените, пожалуйста статью