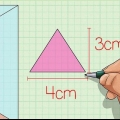
Beispiel: Wenn die Höhe der dreieckigen Basis 5 cm beträgt und die Basis des dreieckigen Prismas 4 cm beträgt, beträgt die Fläche der Basis 1/2 x 5 cm x 4 cm, gleich 10 cm. 

Bsp.: 10 cm x 7 cm = 70 cm 


Bsp.: Länge = 3 cm. 
Bsp.: 3 cm = 3 cm. * 3 cm². * 3 cm². = 27 cm². 


Bsp.: Länge = 10 cm. 
Bsp.: Breite = 8 cm. 
Beispiel: Höhe = 5 cm. 
Beispiel: 10 cm². * 8 cm². * 5cm = 400cm. 


Angenommen Basis 1 = 8 cm, Basis 2 = 6 cm und Höhe = 10 cm. Bsp.: 1/2 x (6 + 8) x 10 = 1/2 x 14 cm x 10 cm = 80 cm. 

80cm x 12cm = 960cm. 


A = 1/2 x 5 x Seite x Apothem A = 1/2 x 5 x 6 cm x 7 cm = 105 cm 

105 cm x 10 cm = 1050 cm 
Berechnung des volumens eines prismas
- Schritte
- Methode 1 von 5: Berechnung des Volumens eines Dreiecksprismas
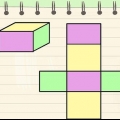
- Methode 2 von 5: Das Volumen eines Würfels berechnen
- Methode 3 von 5: Berechnung des Volumens eines rechteckigen Prismas
- Methode 4 von 5: Berechnung des Volumens eines trapezförmigen Prismas
- Methode 5 von 5: Berechnen Sie das Volumen eines regelmäßigen fünfeckigen Prismas
- Tipps
Ein Prisma ist eine geometrische Figur mit zwei identischen Enden und flachen Seiten. Das Prisma ist nach der Form seiner Grundfläche benannt, daher heißt ein Prisma mit dreieckiger Grundfläche a "dreieckiges Prisma." Um das Volumen eines Prismas zu berechnen, musst du nur die Grundfläche berechnen und mit der Höhe multiplizieren – die Berechnung der Grundfläche kann der knifflige Teil sein. So berechnen Sie das Volumen verschiedener Prismen.
Schritte
Methode 1 von 5: Berechnung des Volumens eines Dreiecksprismas

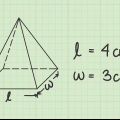
1. Schreiben Sie die Formel zur Bestimmung des Volumens eines dreieckigen Prismas. Die Formel lautet V = 1/2 x Länge x Breite x Höhe. Aber wir zerlegen diese Formel weiter, um die Formel zu erhalten V = Fläche oder Basis x Höhe benutzen. Sie können die Fläche der Basis berechnen, indem Sie die Formel zum Ermitteln der Fläche eines Dreiecks verwenden - multiplizieren Sie 1/2 mit der Länge und Breite der Basis.

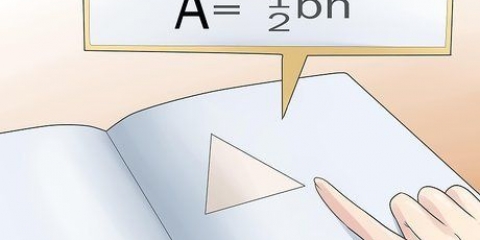
2. Bestimmen Sie die Fläche der Basisebene. Um das Volumen eines Dreiecksprismas zu ermitteln, müssen Sie zunächst die Fläche der Dreiecksbasis bestimmen. Finden Sie die Fläche der Basis des Prismas, indem Sie 1/2 mal die Basis des Dreiecks mal die Höhe multiplizieren.

3. Bestimmen Sie die Höhe. Angenommen, die Höhe dieses dreieckigen Prismas beträgt 7 cm.

4. Multiplizieren Sie die Fläche der dreieckigen Basis mit der Höhe. Multiplizieren Sie die Fläche der Basis mit der Höhe. Multiplizieren Sie die Basis mit der Höhe, und Sie erhalten das Volumen des dreieckigen Prismas.

5. Geben Sie Ihre Antwort in Kubikeinheiten ein. Sie sollten bei der Berechnung eines Volumens immer kubische Einheiten verwenden, da Sie mit dreidimensionalen Objekten arbeiten. Die endgültige Antwort ist 70 cm.
Methode 2 von 5: Das Volumen eines Würfels berechnen

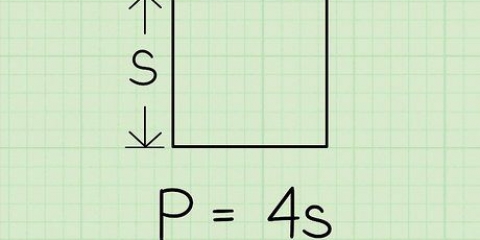
1. Schreiben Sie die Formel zum Bestimmen des Volumens eines Würfels. Die Formel lautet V = Seite. Ein Würfel ist ein Prisma mit 3 gleichen Seiten.

2. Bestimme die Länge von 1 Seite des Würfels. Alle Seiten sind gleich, also ist es egal, welche du wählst.

3. Die Macht der Drei. Multiplizieren Sie die Zahl zweimal mit sich selbst, um die Kubikzahl zu erhalten. Ein Beispiel ist "a x a x a". Da alle Seitenlängen gleich sind, multiplizieren Sie zwei Seiten für die Fläche der Basis und eine dritte Seite für die Höhe. Sie können sich dies als eine Multiplikation der Länge, Breite und Höhe vorstellen, die alle gleich sind.

4. Geben Sie Ihre Antwort in Kubikeinheiten ein.. Die endgültige Antwort ist 27 cm.
Methode 3 von 5: Berechnung des Volumens eines rechteckigen Prismas

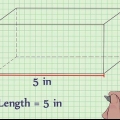
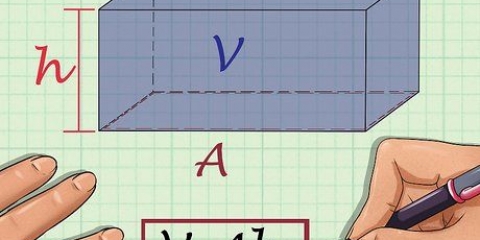
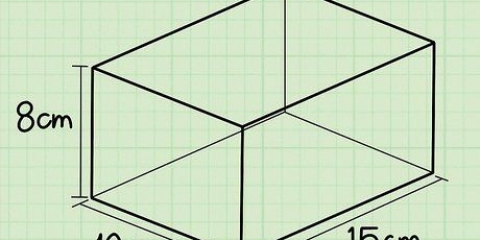
1. Schreiben Sie die Formel zur Bestimmung des Volumens eines rechteckigen Prismas. Die Formel lautet V = Länge * Breite * Höhe. Ein rechteckiges Prisma ist ein Prisma mit einer rechteckigen Grundfläche.

2. Bestimmen Sie die Länge. Die Länge ist die längste Seite der ebenen Fläche des Rechtecks, oberhalb oder unterhalb des rechteckigen Prismas.

3. Bestimmen Sie die Breite. Die Breite des rechteckigen Prismas ist die kürzere Seite der flachen Oberfläche eines Rechtecks, am oberen oder unteren Rand der Form.

4. Bestimmen Sie die Höhe. Die Höhe ist der aufrecht stehende Teil des rechteckigen Prismas. Die Höhe des rechteckigen Prismas kann man sich als den Teil vorstellen, der von einem Rechteck ausgeht und daraus eine dreidimensionale Figur macht.

5. Länge, Breite und Höhe multiplizieren. Multiplizieren Sie diese in beliebiger Reihenfolge für das Produkt. Verwenden Sie diese Methode, um die Fläche der rechteckigen Basis (10 x 8) und dann das Volumen zu ermitteln, indem Sie es mit der Höhe multiplizieren, 5. Um jedoch das Volumen dieses Prismas zu ermitteln, können Sie die Längen der Flächen in beliebiger Reihenfolge multiplizieren.

6. Geben Sie Ihre Antwort in Kubikeinheiten ein. Die endgültige Antwort ist 400 cm.
Methode 4 von 5: Berechnung des Volumens eines trapezförmigen Prismas

1. Schreiben Sie die Formel zur Berechnung des Volumens eines Trapezes. Die Formel lautet: V = [1/2 x (Basis1 + Base2) x Höhe] x Höhe des Prismas. Verwenden Sie den ersten Teil für den Bereich der Basis des Prismas, bevor Sie fortfahren.

2. Finden Sie die Fläche der Basis. Geben Sie dazu die Fläche von oben und unten in die Formel ein, zusammen mit der Höhe.

3. Bestimmen Sie die Höhe des Prismas. Angenommen, die Höhe des Prismas beträgt 12 cm.

4. Multiplizieren Sie die Fläche der Basis mit der Höhe. Um das Volumen des Trapezes zu berechnen, multiplizieren Sie die Fläche der Basis mit der Höhe.

5. Geben Sie Ihre Antwort in Kubikeinheiten ein. Die endgültige Antwort ist 960 cm
Methode 5 von 5: Berechnen Sie das Volumen eines regelmäßigen fünfeckigen Prismas

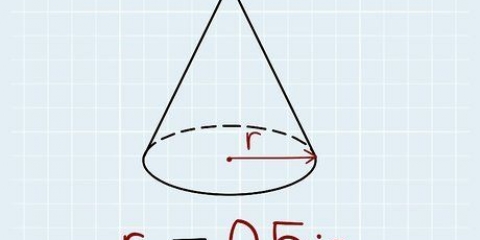
1. Schreiben Sie die Formel zur Bestimmung des Volumens eines regelmäßigen fünfeckigen Prismas auf. Die Formel lautet V = [1/2 x 5 x Seite x Apothem] x Höhe des Prismas. Sie können den ersten Teil der Formel verwenden, um die Fläche der fünfeckigen Basis zu finden. Betrachten Sie dies als die Bestimmung der Fläche der 5 Dreiecke, die zusammen ein regelmäßiges Vieleck bilden. Die Seite hat die Breite von 1 Dreieck und das Apothem ist die Höhe eines der Dreiecke.Du multiplizierst jetzt mit 1/2, weil das ein Teil der Flächenbestimmung eines Dreiecks ist und dann multiplizierst du dies mit 5, weil es 5 Dreiecke in einem Fünfeck gibt.
- Weitere Informationen zur Bestimmung des Apothems finden Sie hier.

2. Finden Sie die Fläche der fünfeckigen Basis. Angenommen, die Länge einer Seite beträgt 6 cm und die Länge des Apothems beträgt 7 cm. Tragen Sie die Zahlen in die Formel ein:

3. Bestimmen Sie die Höhe. Stellen Sie die Höhe der Form auf 10 cm . ein.

4. Multiplizieren Sie die Fläche der fünfeckigen Basis mit der Höhe. Multiplizieren Sie die Fläche der fünfeckigen Basis, 105 cm, mit der Höhe, 10 cm, um das Volumen des gemeinsamen fünfeckigen Prismas zu ermitteln.

5. Geben Sie Ihre Antwort in Kubikeinheiten ein. Die endgültige Antwort ist 1050 cm.
Tipps
- Versuchen "Base" nicht zu verwechseln mit "Basisebene".Eine Basisebene bezieht sich auf die zweidimensionale Form, die die Basis des Prismas ist (normalerweise die Ober- und Unterseite).Aber diese Basisebene kann ihre eigene Basis haben --- eine der Seiten der Form der Ebene, die verwendet wird, um die Fläche dieser Form zu finden.
Оцените, пожалуйста статью