Wenn das Quadrat eine Seite der Länge 4 hat:Umfang = 4 * 4, mit anderen Worten 16. Wenn das Quadrat eine Seite der Länge 6 hat: Umfang = 4 * 6, mit anderen Worten 24. 

Wenn die Fläche des Quadrats 20 beträgt, ist die Seitenlänge S: =√20 oder 4.472 Wenn die Fläche des Quadrats 25 beträgt, ist die Seitenlänge s = √25 oder 5. 
Für ein Quadrat mit einer Fläche von 20 und einer Seitenlänge von 4.473 beträgt der Umfang: Umfang = 4 * 4,472 oder 17.888. Für ein Quadrat mit einer Fläche von 25 und einer Seitenlänge von 5 beträgt der Umfang: Umfang = 4 * 5 oder 20. 


a + a = (2r), jetzt können wir vereinfachen: 2a = 4(r), Jetzt beide Seiten durch 2 teilen: (a) = 2(r), Ziehe nun die Quadratwurzel jeder Seite: a = √(2)r.Unsere Seitenlänge S des eingeschriebenen Quadrats = (2)r. 

Hinweis: Sie hätten es auch so machen können: multiplizieren Sie den Radius (10) mit der Zahl 5.567. 10*5.567 = 56.57, aber weil das schwer zu merken sein könnte, gehen Sie besser den gesamten Prozess durch.
Berechnung des umfangs eines quadrats
Der Umfang einer zweidimensionalen Figur ist der Gesamtabstand um die Figur oder die Summe der Seitenlängen. Die Definition eines Quadrats ist eine Figur mit vier gleichen Seiten und vier rechten Winkeln (90°) zwischen diesen Seiten. Da alle Seiten die gleiche Länge haben, ist es sehr einfach den Umfang eines Quadrats zu bestimmen! In diesem Artikel erfahren Sie zunächst, wie Sie den Umfang eines Quadrats berechnen, wenn Sie die Länge einer seiner Seiten kennen. Dann zeigen wir Ihnen, wie Sie den Umfang berechnen, wenn Sie nur die Fläche kennen, und im letzten Abschnitt zeigen wir Ihnen, wie Sie den Umfang eines einbeschriebenen Quadrats in einem Kreis mit bekannter Radiuslänge berechnen.
Schritte
Methode 1 von 3: Den Umfang eines Quadrats ermitteln, wenn Sie die Länge einer Seite kennen

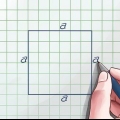
1. Denken Sie an die Formel für den Umfang eines Quadrats. Für ein Quadrat mit der Seitenlänge S der Umfang ist einfach viermal so lang wie diese Seite: Umfang = 4s (Anmerkung: in den Bildern wird der Buchstabe P für Umrisse verwendet, vom englischen `Perimeter`).

2. Finden Sie die Länge einer Seite und multiplizieren Sie sie mit 4, um den Umfang zu finden. Je nach Aufgabe müssen Sie möglicherweise mit einem Lineal messen oder andere Informationen betrachten, um die Länge einer Seite zu bestimmen. Hier sind einige Beispiele für Umfangsberechnungen:
Methode 2 von 3: Den Umfang eines Quadrats bestimmen, wenn Sie seine Fläche kennen

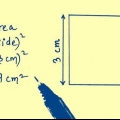
1. Kenne die Formel für die Fläche eines Quadrats. Die Fläche eines beliebigen Rechtecks (denken Sie daran, dass Quadrate spezielle Rechtecke sind) kann als Basis mal Höhe definiert werden.Da Grundfläche und Höhe bei einem Quadrat gleich sind, ist die Fläche eines Quadrats mit Seite S: s*s. Mit anderen Worten: Fläche = s.

2. Ziehe die Quadratwurzel der Fläche. Die Quadratwurzel der Fläche gibt dir die Länge einer der Seiten des Quadrats. Für die meisten Zahlen benötigen Sie einen Taschenrechner, um die Quadratwurzel zu berechnen. Geben Sie zuerst die Zahl ein und drücken Sie dann die Quadratwurzeltaste (√).

3. Multiplizieren Sie die Länge der Seite mit 4, um den Umfang zu ermitteln. Verwenden Sie den Seitenlängenwert, den Sie gerade in der Formel gefunden haben Umfang = 4s. Das Ergebnis ist der Umfang Ihres Quadrats!
Methode 3 von 3: Berechnung des Umfangs eines einbeschriebenen Quadrats in einem Kreis, wenn Sie den Radius kennen

1. Verstehe, was ein eingeschriebenes Quadrat ist. Ein eingeschriebenes Quadrat in einem Kreis ist ein Quadrat, das in einem Kreis gezeichnet ist, wobei alle Ecken des Quadrats den Kreis berühren.

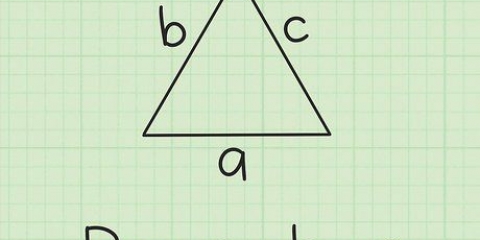
2. Verstehen Sie die Beziehung zwischen dem Radius des Kreises und der Länge der Seiten des Quadrats. Der Abstand von der Mitte eines eingeschriebenen Quadrats zu einer beliebigen Ecke ist gleich dem Radius des Kreises. Zur Seitenlänge S Um das herauszufinden, müssen wir uns zunächst vorstellen, dass wir das Quadrat diagonal halbieren, sodass zwei gleichseitige Dreiecke entstehen. Diese Dreiecke haben gleiche Seiten ein und B und eine Hypotenuse C, von dem wir wissen, dass er dem doppelten Radius des Kreises entspricht, d. h 2r.

3. Verwenden Sie den Satz des Pythagoras, um die Seitenlänge des Quadrats zu bestimmen. Der Satz des Pythagoras lautet wie folgt: In einem rechtwinkligen Dreieck ist die Summe der Quadrate der Längen der rechteckigen Seiten (a, b) gleich dem Quadrat der Länge der Hypotenuse (c), a + b = c. Weil Seiten ein und B gleich sind (wir haben es immer noch mit einem Quadrat zu tun!) und das wissen wir c=2r Wir können nun die Gleichung aufschreiben und vereinfachen, um die Länge einer Seite zu ermitteln:

4. Multiplizieren Sie die Länge einer Seite des Quadrats mit vier, um den Umfang zu finden. In diesem Fall beträgt der Umfang des Quadrats: Umfang = 4√(2)r. Der Umfang eines eingeschriebenen Quadrats in einem Kreis ist daher immer gleich 4√(2)r, also etwa 5,657r

5. Eine Beispielfrage lösen. Wir nehmen ein eingeschriebenes Quadrat in einem Kreis mit einem Radius von 10. Das bedeutet die Diagonale des Quadrats = 2(10) oder 20. Der Satz des Pythagoras lehrt uns: 2(a) = 20, So 2a = 400. Jetzt beide Seiten durch zwei teilen, wir sehen das a = 200. Ziehe die Quadratwurzel jeder Seite und wir sehen das a = 14,142. Multiplizieren Sie dies mit 4, um den Umfang Ihres Quadrats zu ermitteln: Umfang = 56,57.
"Berechnung des umfangs eines quadrats"
Оцените, пожалуйста статью