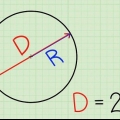
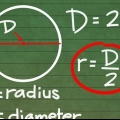
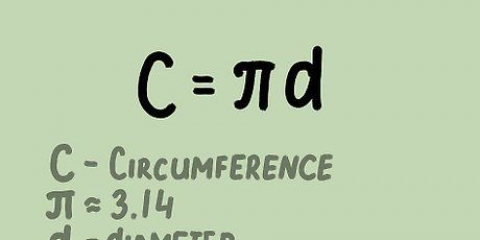Der Radius (R) eines Kreises ist der Abstand von einem Punkt auf dem Kreis zum Mittelpunkt des Kreises. Der Durchmesser (D) eines Kreises ist der Abstand von einem Punkt auf dem Kreis zu einem anderen Punkt direkt gegenüber dem Kreis, der durch den Mittelpunkt des Kreises geht. Der griechische Buchstabe pi (π) steht für das Verhältnis des Umfangs geteilt durch den Durchmesser und wird durch die Zahl 3.14159265 . dargestellt..., eine irrationale Zahl, die weder eine letzte Ziffer noch ein erkennbares Muster aus sich wiederholenden Ziffern hat. Diese Zahl wird für Standardberechnungen oft auf 3,14 gerundet. 
In den meisten mathematischen Aufgaben wird der Radius oder Durchmesser angegeben. 
Zum Beispiel: Wie groß ist der Umfang eines Kreises mit einem Radius von 3 cm? Schreiben Sie die Formel: C = 2πr Füllen Sie die Variablen aus: C = 2π3 Multiplizieren: C = (2*3*π) = 6π = 18,84 cm Zum Beispiel: Wie groß ist der Umfang eines Kreises mit einem Durchmesser von 9 m? Schreiben Sie die Formel auf: C = πd Tragen Sie die Variablen ein: C = 9π Multiplizieren: C = (9*π) = 28,26 m 
Bestimmen Sie den Umfang eines Kreises mit einem Durchmesser von 5 m. C = πd = 5π = 15,7 m Bestimmen Sie den Umfang eines Kreises mit einem Radius von 10 m. C = 2πr = C = 2π10 = 2 *10 *π = 62,8 m. 

Der Radius (R) eines Kreises ist der Abstand von einem Punkt auf dem Kreis zum Mittelpunkt des Kreises. Der Durchmesser (D) eines Kreises ist der Abstand von einem Punkt auf dem Kreis zu einem anderen Punkt direkt gegenüber dem Kreis, der durch den Mittelpunkt des Kreises geht. Der griechische Buchstabe pi (π) steht für das Verhältnis des Umfangs geteilt durch den Durchmesser und wird durch die Zahl 3.14159265 . dargestellt..., eine irrationale Zahl, die weder eine letzte Ziffer noch ein erkennbares Muster aus sich wiederholenden Ziffern hat. Diese Zahl wird für grundlegende Berechnungen normalerweise auf 3,14 gerundet. 
In den meisten mathematischen Aufgaben wird der Radius oder Durchmesser angegeben. 
Zum Beispiel: Was ist die Fläche eines Kreises mit einem Radius von 3 m? Schreiben Sie die Formel: A = r. Füllen Sie die Variablen aus: A = π3. Den Radius quadrieren: R = 3 = 9 Mit pi multiplizieren: ein = 9π = 28,26 m Zum Beispiel: Was ist die Fläche eines Kreises mit einem Durchmesser von 4 m? Schreiben Sie die Formel: A = π(d/2). Füllen Sie die Variablen aus: A = π(4/2). Teilen Sie den Durchmesser durch 2: d/2 = 4/2 = 2 Quadriere das Ergebnis: 2 = 4 Mit pi multiplizieren: ein = 4π = 12,56 m 
Finden Sie die Fläche eines Kreises mit einem Durchmesser von 7 m. A = π(d/2) = π(7/2) = π(3,5) = 12,25 * π= 38,47 m. Finden Sie die Fläche eines Kreises mit einem Radius von 3 m. A = πr = π * 3 = 9 * π = 28,26 m 

Zum Beispiel: Berechne den Umfang eines Kreises mit einem Radius von (x + 1). Schreiben Sie die Formel: C = 2πr Geben Sie die angegebenen Informationen ein: C = 2π(x+1) 
Beispiel: Berechne den Umfang eines Kreises mit einem Radius von (x = 1). C = 2πr = 2π(x+1) = 2πx + 2π1 = 2πx +2π = 6,28x + 6,28 Wenn der Wert von `x` später im Problem angegeben wird, können Sie ihn einstecken und eine ganze Zahl erhalten. 
Finden Sie die Fläche eines Kreises mit einem Radius von 2x. A = πr = π(2x) = π4x = 12,56x Finden Sie die Fläche eines Kreises mit einem Durchmesser von (x + 2). A = π(d/2) = π(((x +2)/2) = ((x +2)/4)π
Berechnen des umfangs und der fläche eines kreises
Der Umfang (C) eines Kreises ist sein Umfang oder der Abstand um ihn herum. Die Fläche (A) eines Kreises gibt an, wie viel Platz der Kreis einnimmt oder die vom Kreis eingeschlossene Fläche. Sowohl Fläche als auch Umfang lassen sich mit einfachen Formeln aus dem Radius bzw. Durchmesser des Kreises und dem Wert von pi . berechnen.
Schritte
Teil 1 von 3: Berechnung des Umfangs

1. Lerne die Formel für den Umfang eines Kreises. Um den Umfang eines Kreises zu berechnen, gibt es zwei Formeln: C = 2πr oder C = d, wobei π die mathematische Konstante und ungefähr gleich 3,14 . ist,R gleich dem Radius ist und D gleich dem Durchmesser.
- Da der Radius eines Kreises gleich dem doppelten Durchmesser ist, sind diese Gleichungen im Wesentlichen gleich.
- Die Einheiten für den Umfang können eine beliebige Einheit für das Längenmaß sein: Kilometer, Meter, Zentimeter usw.

2. Verstehe die verschiedenen Teile der Formel. Es gibt drei Komponenten, um den Umfang eines Kreises zu bestimmen: Radius, Durchmesser und. Der Radius und der Durchmesser hängen zusammen: Der Radius ist gleich dem halben Durchmesser, während der Durchmesser gleich dem doppelten Radius ist.

3. Messen Sie den Radius oder Durchmesser des Kreises. Legen Sie ein Lineal auf eine Kante des Kreises, durch die Mitte und auf die andere Seite des Kreises. Der Abstand vom Mittelpunkt des Kreises ist der Radius, während der Abstand vom anderen Ende des Kreises der Durchmesser ist.

4. Verarbeite und löse die Variablen. Nachdem Sie den Radius und/oder Durchmesser des Kreises bestimmt haben, können Sie diese Variablen in die entsprechende Gleichung einsetzen. Wenn Sie den Strahl haben, verwenden Sie C = 2πr, aber wenn du den durchmesser kennst dann benutze C = d.

5. Üben Sie mit ein paar Beispielen. Nachdem Sie die Formel gelernt haben, ist es an der Zeit, mit einigen Beispielen zu üben. Je mehr Probleme Sie lösen, desto einfacher wird es in Zukunft sein, sie zu lösen.
Teil 2 von 3: Flächenberechnung

1. Lerne die Formel für die Fläche eines Kreises. Die Fläche eines Kreises kann entweder anhand seines Durchmessers oder seines Radius mit zwei verschiedenen Formeln berechnet werden: A = r oder A = π(d/2), wobei π die mathematische Konstante ungefähr gleich 3,14 . ist,R der Radius und D der Durchmesser.
- Da der Radius eines Kreises gleich dem halben Durchmesser ist, sind diese Gleichungen im Wesentlichen gleich.
- Die Einheiten für die Fläche können eine beliebige Einheit für die Länge zum Quadrat sein: km zum Quadrat (km), Meter zum Quadrat (m), Zentimeter zum Quadrat (cm) usw.

2. Verstehe die verschiedenen Teile der Formel. Es gibt drei Komponenten, um den Umfang eines Kreises zu bestimmen: Radius, Durchmesser und. Der Radius und der Durchmesser stehen in Beziehung zueinander: Der Radius ist gleich dem halben Durchmesser, während der Durchmesser gleich dem doppelten Radius ist.

3. Messen Sie den Radius oder Durchmesser des Kreises. Platzieren Sie ein Ende eines Lineals an einem Punkt auf dem Kreis, durch die Mitte und auf die andere Seite des Kreises. Der Abstand vom Mittelpunkt des Kreises ist der Radius, während der Abstand vom anderen Punkt auf dem Kreis der Durchmesser ist.

4. Fülle die Variablen aus und löse sie. Nachdem Sie den Radius und/oder den Durchmesser des Kreises bestimmt haben, können Sie diese Variablen in die entsprechende Gleichung einsetzen. Wenn Sie den Radius kennen, verwenden Sie A = r, aber wenn du den durchmesser kennst dann benutze A = π(d/2).

5. Üben Sie mit ein paar Beispielen. Nachdem Sie die Formel gelernt haben, ist es an der Zeit, mit einigen Beispielen zu üben. Je mehr Probleme Sie lösen, desto einfacher können Sie andere Probleme lösen.
Teil 3 von 3: Flächen- und Umfangsberechnung mit Variablen

1. Bestimmen Sie den Radius oder Durchmesser des Kreises. Einige Probleme geben einen Radius oder Durchmesser mit einer Variablen wie r = (x + 7) oder d = (x + 3). In diesem Fall können Sie immer noch die Fläche oder den Umfang bestimmen, aber Ihre endgültige Antwort enthält auch diese Variable. Notieren Sie den Radius oder Durchmesser wie in der Erklärung angegeben.
- Beispiel: Berechne den Umfang eines Kreises mit einem Radius von (x = 1).

2. Schreiben Sie die Formel mit den gegebenen Informationen. Egal, ob Sie Fläche oder Umfang berechnen möchten, Sie befolgen immer noch die grundlegenden Schritte zum Ausfüllen Ihres Wissens. Schreiben Sie die Formel für Fläche oder Umfang und tragen Sie dann die gegebenen Variablen ein.

3. Lösen Sie das Problem, als ob die Variable eine Zahl wäre. An dieser Stelle können Sie das Problem einfach wie gewohnt lösen und die Variable so behandeln, als wäre es nur eine andere Zahl. Vielleicht brauchst du die Verteilungseigenschaft verwenden um die endgültige Antwort zu vereinfachen.

4. Üben Sie mit einigen Beispielen. Nachdem Sie die Formel gelernt haben, ist es an der Zeit, mit einigen Beispielen zu üben. Je mehr Probleme Sie lösen, desto einfacher ist es, neue zu lösen.
"Berechnen des umfangs und der fläche eines kreises"
Оцените, пожалуйста статью