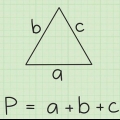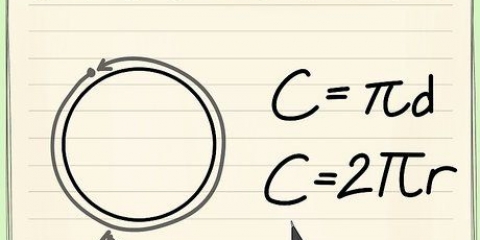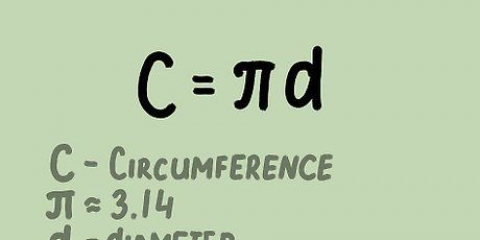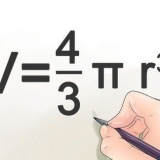Wenn beispielsweise der Durchmesser eines Kreises 4 beträgt, dann ist die Gerade 4/2 oder 2. 

Wenn der Umfang beispielsweise 15 beträgt, ist der Radius r = 15/2π oder 2,39. 


a = √(3 + 4) a = √(9 + 16) a = √25 a = 5 
b= √(-7 + -6) b = √(49 + 36) b = √85 b = 9.23 
c= √(4 + 2) c = √(16 + 4) c = √20 c = 4.47 
Die Längen des Dreiecks sind wie folgt: a = 5, b = 9.23 und c = 4.47. Die Formel für den Radius sieht also so aus: r = (5 * 9.23*4.47)/(√(5 + 4.47 + 9.23)(4.47 + 9.23 - 5)(9.23 + 5 - 4.47)(5 + 4.47 – 9.23)). 
(a * b * c) = (5 * 9.23*4.47) = 206.29 r = (206.29)/(√(5 + 4.47 + 9.23)(4.47 + 9.23 - 5)(9.23 + 5 - 4.47)(5 + 4.47 – 9.23)) 
(a + b + c) = (5 + 4.47 + 9.23) = 18.7 (b + c - a) = (4.47 + 9.23 - 5) = 8.7 (c + a - b) = (9.23 + 5 - 4.47) = 9.76 (a + b - c) = (5 + 4.47 – 9.23) = 0.24 r = (206.29)/(√(18.7)(8.7)(9.76)(0.24)) 
(18.7)(8.7)(9.76)(0.24) = 381.01 r = 206.29/√381.01 
√381.01 = 19.51 r = 206.29/19.52 
r = 10.57
Berechnung des radius eines kreises
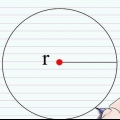
Der Radius eines Kreises ist der Abstand vom Mittelpunkt des Kreises zum Rand. Der Durchmesser eines Kreises ist die Länge der geraden Linie, die zwischen zwei Punkten auf der Kugel oder dem Kreis und durch deren Mittelpunkt gezogen werden kann.Sie werden oft gebeten, den Radius eines Kreises basierend auf anderen Daten zu berechnen. In diesem Artikel erfahren Sie, wie Sie den Radius eines Kreises basierend auf einem gegebenen Durchmesser, Umfang und Fläche berechnen. Die vierte Methode ist eine fortschrittlichere Methode zur Bestimmung des Mittelpunkts und des Radius eines Kreises basierend auf den Koordinaten von drei Punkten auf dem Kreis.
Schritte
Methode 1 von 3: Berechnen Sie den Radius, wenn Sie den Durchmesser kennen

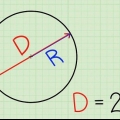
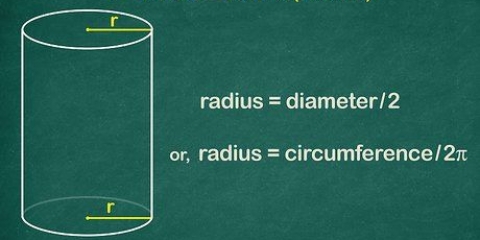
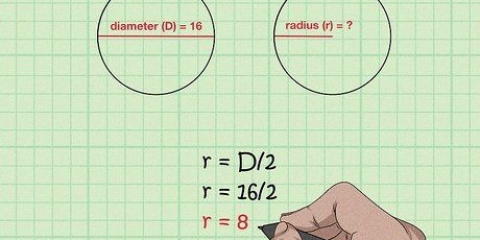
1. Erinnere dich an den Durchmesser. Der Durchmesser eines Kreises ist die Länge der geraden Linie, die zwischen zwei Punkten auf der Kugel oder dem Kreis und durch deren Mittelpunkt gezogen werden kann. Der Durchmesser ist die längste Linie, die durch einen Kreis gezogen werden kann und teilt den Kreis in zwei Hälften. Die Länge des Durchmessers ist auch gleich der Länge des doppelten Radius. Die Formel für den Durchmesser lautet: D= 2r, wobei "D" steht für Durchmesser und "R" für Balken. Die Formel für den Radius lässt sich aus der vorherigen Formel ableiten und lautet daher: r = D/2.

2. Teilen Sie den Durchmesser durch 2, um den Radius zu finden. Wenn Sie den Durchmesser eines Kreises kennen, müssen Sie ihn nur durch 2 teilen, um den Radius zu ermitteln.
Methode 2 von 3: Berechnen Sie den Radius, wenn Sie den Umfang kennen

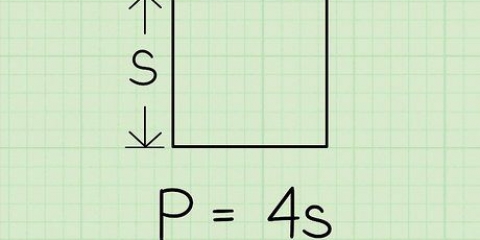
1. Erinnerst du dich an die Formel für den Umfang eines Kreises?. Der Umfang eines Kreises ist der Abstand um den Kreis. Eine andere Betrachtungsweise ist: Der Umfang ist die Länge der Linie, die man erhält, wenn man den Kreis an einem Punkt aufschneidet und die Linie gerade legt. Die Formel für den Umfang eines Kreises lautet O = 2πr, wobei "R" ist der Radius und π ist die Konstante pi oder 3,14159... Die Formel für den Radius lautet dann r = O/2π.
- Normalerweise kannst du Pi auf zwei Nachkommastellen (3,14) runden, aber frage zuerst deinen Lehrer.

2. Berechnen Sie den Radius mit dem angegebenen Umfang. Um den Radius basierend auf dem Umfang zu berechnen, teilen Sie den Umfang durch 2π oder 6,28
Methode 3 von 3: Berechnen Sie den Radius, wenn Sie die Koordinaten von drei Punkten auf dem Kreis kennen

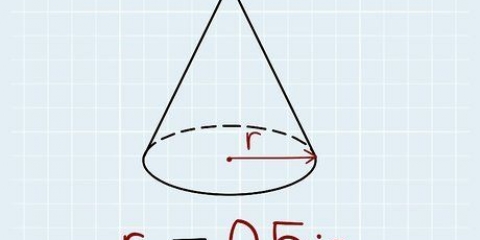
1. Verstehe, dass drei Punkte einen Kreis definieren können. Drei beliebige Punkte auf einem Gitter definieren eine Kreistangente zu den drei Punkten. Es ist der umschriebene Kreis des Dreiecks, das die Punkte bildet. Der Kreismittelpunkt kann je nach Lage der drei Punkte innerhalb oder außerhalb des Dreiecks liegen und ist gleichzeitig der "Überschneidung" des Dreiecks.Es ist möglich, den Radius des Kreises zu berechnen, wenn Sie die xy-Koordinaten der drei fraglichen Punkte kennen.
- Nehmen wir als Beispiel drei Punkte, die wie folgt definiert sind: P1 = (3,4), P2 = (6, 8) und P3 = (-1, 2).

2. Verwenden Sie die Abstandsformel, um die Längen der drei Seiten des Dreiecks zu berechnen, die wir a, b und c nennen. Die Formel für den Abstand zwischen zwei Koordinaten (x1, ja1) und (x2, ja2) ist wie folgt: Abstand = √(( x2 - x1) + (ja2 - ja1)). Verarbeite nun die Koordinaten der drei Punkte in dieser Formel, um die Längen der drei Seiten des Dreiecks zu ermitteln.

3. Berechnen Sie die Länge der ersten Seite a, die vom Punkt P1 nach P2 verläuft. In unserem Beispiel sind die Koordinaten von P1 (3.4) und von P2 (6.8), also die Seitenlänge a = √((6 - 3) + (8 - 4)).

4. Wiederholen Sie den Vorgang, um die Länge der zweiten Seite b zu finden, die von P2 bis P3 verläuft. In unserem Beispiel sind die Koordinaten von P2 (6.8) und von P3 (-1.2), also die Länge der Seite b = √((-1 - 6) + (2 - 8)).

5. Wiederholen Sie den Vorgang, um die Länge der dritten Seite c zu finden, die von P3 bis P1 verläuft. In unserem Beispiel sind die Koordinaten von P3 (-1,2) und von P1 (3,4), also die Seitenlänge c =√(((3 - -1) + (4 - 2)).

6. Verwenden Sie diese Längen in der Radiusfindungsformel: (abc)/(√(a + b + c)(b + c - a)(c + a - b)(a + b - c)).. Das Ergebnis ist der Radius unseres Kreises!

7. Multiplizieren Sie zuerst die drei Längen miteinander, um den Zähler des Bruchs zu finden. Dann passt du die Formel an.

8. Berechne die Summen in Klammern. Trage die Ergebnisse dann in die Formel ein.

9. Multiplizieren Sie die Werte im Nenner.

10. Ziehen Sie die Quadratwurzel des Produkts, um den Nenner des Bruchs zu finden.

11. Teilen Sie nun den Zähler durch den Nenner, um den Radius des Kreises zu finden!
"Berechnung des radius eines kreises"
Оцените, пожалуйста статью