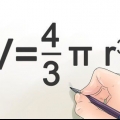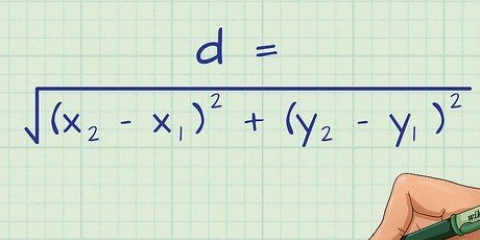Wenn Sie eine Kugel mit einem Umfang von 20 m haben, finden Sie den Radius mit 20/2π = 3,183 m. Sie können dieselbe Formel verwenden, um zwischen dem Radius und dem Umfang eines Kreises umzurechnen. 
Wenn Sie eine Kugel mit einem Volumen von 100 cm haben, erhalten Sie den Radius wie folgt: ((V/π)(3/4)) = r ((100/π)(3/4)) = r ((31.83)(3/4)) = r (23.87) = r 2.88 = r 
Wenn Sie eine Kugel mit einer Fläche von 1200 cm haben, berechnen Sie den Radius wie folgt: (A/(4π)) = r (1200/(4π)) = r (300/(π)) = r (95,49) = r 9,77 cm = r 

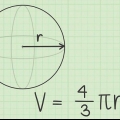
D = 2r. So wie Kreise ist der Durchmesser einer Kugel das Doppelte ihres Radius. C = πD oder 2πr. So wie Kreise ist der Umfang einer Kugel gleich π mal dem Durchmesser. Da der Durchmesser doppelt so groß ist wie der Radius, können wir auch sagen, dass der Umfang gleich dem doppelten Radius mal π . ist. V = (4/3)πr. Das Volumen einer Kugel ist ihr Radius zum Würfel (r x r x r), mal π mal 4/3. A = 4πr. Die Fläche einer Kugel ist ihr Radius in zweiter Potenz (r x r), mal π, mal 4. Da der Umfang eines Kreises gleich πr ist, kann man auch sagen, dass die Fläche einer Kugel gleich dem Vierfachen der Fläche eines Kreises ist, die durch seinen Umfang gebildet wird. 

Im Kontext unserer Beispielaufgabe stellen wir fest, dass der Punkt (3, 3, 0) auf der Kugeloberfläche ist gegeben. Durch Berechnung des Abstands zwischen diesem Punkt und dem Mittelpunkt können wir den Radius ermitteln. 
In unserem Beispiel ersetzen wir (4, -1, 12) durch (x1,ja1,z1) und (3, 3, 0) für (x2,ja2,z2), wobei wir dies wie folgt lösen: d = √((x2 - x1) + (ja2 - ja1) + (z2 - z1)) d = (((3 - 4) + (3 - -1) + (0 - 12)) d = ((-1) + (4) + (-12)) d = √(1 + 16 + 144) d = √(161) d = 12,69. Dies ist der Radius unserer Kugel. 
Durch Quadrieren beider Seiten dieser Gleichung erhalten wir: r = (x2 - x1) + (ja2 - ja1) + (z2 - z1). Hinweis: Dies entspricht im Wesentlichen der Standardgleichung für eine Kugel (r = x + y + z), vorausgesetzt, ihr Mittelpunkt ist gleich (0,0,0).
Berechnung des radius einer kugel
Der Radius einer Kugel (abgekürzt als Variable R oder R) ist der Abstand vom genauen Mittelpunkt der Kugel zu einem Punkt auf der Oberfläche dieser Kugel. So wie Kreise, der Radius einer Kugel ist oft eine wesentliche erste Kenngröße für die Berechnung von Durchmesser, Umfang, Fläche und Volumen einer Kugel. Sie können jedoch auch vom Durchmesser, Umfang usw. rückwärts arbeiten. um den Radius der Kugel zu finden. Verwenden Sie die Formel, die für Ihre Daten geeignet ist.
Schritte
Methode 1 von 3: Verwenden von Radiusformeln

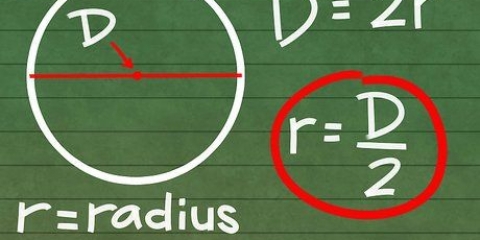
1. Bestimmen Sie den Radius, wenn Sie den Durchmesser kennen. Der Radius ist ein halber Durchmesser, also verwenden Sie die Formel r = D/2. Dies ist identisch mit der Methode zur Berechnung des Radius eines Kreises bei gegebenem Durchmesser.
- Wenn Sie eine Kugel mit einem Durchmesser von 16 cm haben, berechnen Sie den Radius mit 16/2 = 8 cm². Wenn der Durchmesser 42 beträgt, ist der Radius 21.

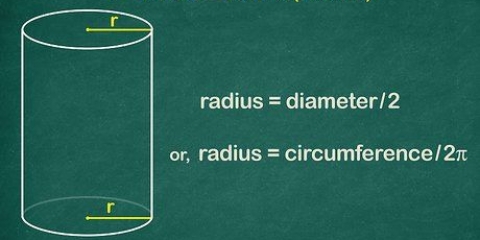
2. Bestimmen Sie den Radius, wenn Sie den Umfang kennen. Verwenden Sie die Formel C/2π. Da der Umfang gleich πD ist, was wiederum gleich 2πr ist, berechnen Sie den Radius, indem Sie den Umfang durch 2π . dividieren.

3. Berechnen Sie den Radius, wenn Sie das Volumen der Kugel kennen. Verwenden Sie die Formel ((V/π)(3/4)). Das Volumen einer Kugel ergibt sich aus der Gleichung V = (4/3)πr.Durch Auflösen der Gleichung nach r erhält man ((V/π)(3/4)) = r, damit wird klar, dass der Radius einer Kugel gleich dem Volumen dividiert durch π, mal 3/4 , zu 1/3 Potenz (oder Kubikwurzel).

4. Bestimmen Sie den Radius der Oberfläche. Verwenden Sie die Formel r = √(A/(4π)). Die Fläche einer Kugel wird mit der Gleichung A = 4πr . berechnet. Das Auflösen der Gleichung nach r ergibt √(A/(4π)) = r, was bedeutet, dass der Radius einer Kugel gleich der Quadratwurzel ihrer Fläche geteilt durch 4π . ist. Sie können auch (A/(4π)) auf 1/2 für das gleiche Ergebnis erhöhen.
Methode 2 von 3: Definieren von Schlüsselbegriffen

1. Kennen Sie die Grundabmessungen einer Kugel. Der Radius (R) ist der Abstand vom genauen Mittelpunkt der Kugel zu einem beliebigen Punkt auf der Kugeloberfläche. Im Allgemeinen können Sie den Radius einer Kugel bestimmen, wenn Sie ihren Durchmesser, Umfang, Volumen oder Fläche kennen.
- Durchmesser (D): die Länge der Linie durch den Mittelpunkt einer Kugel & ndash; doppelter Radius. Der Durchmesser ist die Länge einer Linie durch den Kugelmittelpunkt: von einem Punkt an der Außenseite der Kugel zu einem entsprechenden Punkt direkt gegenüber. Mit anderen Worten, der größtmögliche Abstand zwischen zwei Punkten auf der Kugel.
- Umfang (C): der eindimensionale Abstand um die Kugel an ihrer breitesten Stelle. Mit anderen Worten, der Umfang des kreisförmigen Querschnitts einer Kugel, deren Ebene durch den Mittelpunkt der Kugel geht.
- Volumen (V): der dreidimensionale Raum innerhalb der Kugel. Es ist der "von der Kugel eingenommener Raum".
- Bereich (A): der zweidimensionale Raum auf der äußeren Oberfläche der Kugel. Die Menge an flachem Raum, die die Außenseite der Kugel bedeckt.
- pi (π): eine Konstante, die das Verhältnis des Kreisumfangs zum Kreisdurchmesser ausdrückt. Die ersten 10 Ziffern von Pi sind immer 3.141592653, obwohl dies normalerweise auf gerundet wird 3.14.

2. Verwenden Sie verschiedene Messwerte, um den Radius zu bestimmen. Sie können Durchmesser, Umfang, Volumen und Fläche verwenden, um den Radius einer Kugel zu berechnen. Wenn Sie die Länge des Radius kennen, können Sie jede dieser Zahlen berechnen. Um den Radius zu ermitteln, können Sie die Formeln zur Berechnung dieser Teile umkehren. Lernen Sie die Formeln mit Radius, um Durchmesser, Umfang, Fläche und Volumen zu berechnen.
Methode 3 von 3: Ermitteln des Radius als Abstand zwischen zwei Punkten

1. Bestimmen Sie die Koordinaten (x, y, z) des Kugelmittelpunkts. Eine Möglichkeit, sich den Radius einer Kugel vorzustellen, ist der Abstand zwischen dem Mittelpunkt der Kugel und einem beliebigen Punkt auf ihrer Oberfläche. Da dies der Fall ist, können Sie den Radius der Kugel anhand der Koordinaten des Mittelpunkts und eines Punktes auf der Kugeloberfläche bestimmen, indem Sie den Abstand zwischen den beiden Punkten mit einer Variante der Standardabstandsformel berechnen. Finden Sie zunächst die Koordinaten des Mittelpunkts der Kugel. Beachten Sie, dass eine Kugel dreidimensional ist, dies ist ein (x, y, z)-Punkt anstelle eines (x, y)-Punkts.
- An einem Beispiel ist das leichter zu verstehen. Angenommen, eine Kugel sei gegeben mit als Mittelpunkt(-1, 4, 12). In den nächsten Schritten werden wir diesen Punkt bei der Bestimmung des Radius verwenden.

2. Bestimmen Sie die Koordinaten eines Punktes auf der Kugeloberfläche. Dann müssen Sie die (x, y, z) Koordinaten eines Punktes auf der Kugeloberfläche bestimmen. Das ist möglich jeder Punkt auf der Kugeloberfläche. Da per Definition alle Punkte auf der Oberfläche einer Kugel gleich weit vom Mittelpunkt entfernt sind, können Sie jeden beliebigen Punkt verwenden, um den Radius zu bestimmen.

3. Bestimmen Sie den Radius mit der Formel d = √((x2 - x1) + (ja2 - ja1) + (z2 - z1)). Da Sie nun den Mittelpunkt der Kugel und einen Punkt auf der Kugeloberfläche kennen, können Sie den Radius ermitteln, indem Sie den Abstand zwischen ihnen berechnen. Verwenden Sie die dreidimensionale Abstandsformel d = √(((x2 - x1) + (ja2 - ja1) + (z2 - z1)), wobei d der Abstand ist, (x1,ja1,z1) stellt die Koordinaten des Mittelpunkts dar, und(x2,ja2,z2) steht für die Koordinaten des Punktes auf der Fläche, um den Abstand zwischen beiden Punkten zu bestimmen.

4. Wissen Sie, dass im Allgemeinen r = √((x2 - x1) + (ja2 - ja1) + (z2 - z1)). In einer Kugel hat jeder Punkt auf der Oberfläche den gleichen Abstand vom Mittelpunkt der Kugel. Nehmen wir die obige dreidimensionale Distanzformel und ersetzen die Variable "D" durch die Variable "R" des Radius, dann erhalten wir eine Gleichung, die es uns ermöglicht, den Radius an jedem gegebenen Mittelpunkt (x1,ja1,z1) und jeder entsprechende Punkt auf der Oberfläche (x2,ja2,z2).
Tipps
- Die Reihenfolge der Operationen ist wichtig. Wenn Sie sich nicht sicher sind, wie die mathematischen Regeln funktionieren und Ihr Taschenrechner Klammern unterstützt, stellen Sie sicher, dass Sie diese verwenden.
- Dieser Artikel wurde erstellt, weil dieses Thema sehr gefragt war. Wenn Sie jedoch zum ersten Mal versuchen, die räumliche Geometrie zu verstehen, ist es wahrscheinlich besser, mit der anderen Seite zu beginnen: die Eigenschaften einer Kugel zu berechnen, wenn ihr Radius gegeben ist.
- Pi oder π ist ein griechischer Buchstabe, der das Verhältnis des Durchmessers eines Kreises zu seinem Umfang angibt. Es ist eine irrationale Zahl und kann nicht als Verhältnis von reellen Zahlen geschrieben werden. Es gibt viele Näherungen, und 333/106 gibt Pi auf vier Dezimalstellen an. Heute erinnern sich die meisten Menschen an die Näherung 3.14, die für alltägliche Zwecke normalerweise genau genug ist.
"Berechnung des radius einer kugel"
Оцените, пожалуйста статью