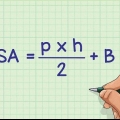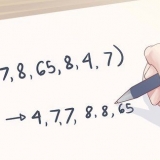Das Volumen einer Pyramide berechnen: 8 Schritte (mit Bildern)

Schritte
- Methode 1 von 2: Pyramide mit rechteckiger Grundfläche
- Methode 2 von 2: Pyramide mit dreieckiger Basis
Tipps
Warnungen

Um das Volumen einer Pyramide zu berechnen, multiplizieren Sie die Fläche der Basis mit der Höhe der Pyramide. Teile das Ergebnis durch 3, das ist alles! Lesen Sie diesen Artikel mit Berechnungsmethoden für eine Pyramide mit rechteckiger Grundfläche und eine Pyramide mit dreieckiger Grundfläche.

Schritte

Methode 1 von 2: Pyramide mit rechteckiger Grundfläche

Bildtitel Berechnen Sie das Volumen einer Pyramide Schritt 1

1. Bestimmen Sie die Länge und Breite der Basis. In diesem Beispiel beträgt die Länge 4 cm und die Breite 3 cm. Wenn Sie eine quadratische Basis haben, ist die Methode dieselbe, nur die Länge und Breite sind gleich. Schreibe deine Maße auf.

Bildtitel Berechnen Sie das Volumen einer Pyramide Schritt 2

2. Multiplizieren Sie die Länge mit der Breite, um die Fläche der Basis zu berechnen. Um die Fläche unseres Beispiels zu berechnen, multiplizieren wir 3 cm mit 4 cm. 3cm x 4cm = 12cm

Bildtitel Berechnen Sie das Volumen einer Pyramide Schritt 3

3. Multiplizieren Sie die Fläche der Basis mit der Höhe. Die Grundfläche beträgt 12 cm und die Höhe 4 cm, also multiplizieren wir 12 cm mit 4 cm. 12cm x 4cm = 48cm

Bildtitel Berechnen Sie das Volumen einer Pyramide Schritt 4

4. Teilen Sie das Ergebnis durch 3. Das entspricht der Multiplikation mit 1/3. 48cm/3 = 16cm. Das Volumen einer Pyramide mit einer Höhe von 4 cm und einer rechteckigen Grundfläche mit einer Breite von 3 cm und einer Länge von 4 cm beträgt demnach 16 cm. Vergessen Sie nicht, das Ergebnis in Kubikeinheiten anzugeben.

Methode 2 von 2: Pyramide mit dreieckiger Basis

Bild mit dem Titel Berechnen Sie das Volumen einer Pyramide Schritt 5

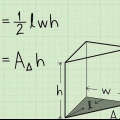
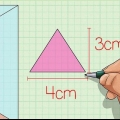
1. Bestimmen Sie die Länge und Breite der Basis. Die Länge und Breite der Basis muss senkrecht zueinander, sonst funktioniert diese Methode nicht. Sie können auch als die Unterseite und die Höhe des Dreiecks angesehen werden. In diesem Beispiel beträgt die Breite des Dreiecks 2 cm und die Länge 4 cm. Schreib das auf.

Bildtitel Berechnen Sie das Volumen einer Pyramide Schritt 6

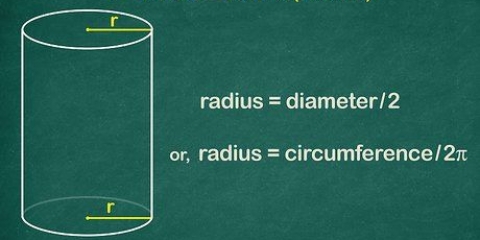
2. Berechnen Sie die Fläche der Basis. Um die Fläche der Basis zu berechnen, verwenden wir die folgende Formel:A = 1/2(o)(h). So machen wir es:

A = 1/2(o)(h)

A = 1/2(2)(4)

A = 1/2(8)

A = 4 cm

Bildtitel Berechnen Sie das Volumen einer Pyramide Schritt 7

3. Multiplizieren Sie die Fläche der Basis mit der Höhe der Pyramide. Die Grundfläche beträgt 4 cm und die Höhe beträgt 5 cm. 4cm x 5cm = 20cm.

Bildtitel Berechnen Sie das Volumen einer Pyramide Schritt 8

4. Teilen Sie das Ergebnis durch 3. 20cm/3 = 6,67cm. Das Volumen einer Pyramide mit einer Höhe von 5 cm und einer dreieckigen Grundfläche mit einer Breite von 2 cm und einer Länge von 4 cm beträgt demnach 6,67 cm.

Tipps

Bei einer Pyramide mit quadratischer Grundfläche sind die Höhe, die Linie, die die dreieckige Seite in zwei gleiche Dreiecke teilt, und die Breite der Grundfläche durch den Satz des Pythagoras verbunden: (Breite ÷ 2) + (Höhe) = (Höhe des Dreiecks)
Diese Methode kann auch auf Objekte wie fünfeckige Pyramiden, sechseckige Pyramiden usw. angewendet werden. Der allgemeine Prozess ist: A) Berechnen Sie die Fläche der Basis; B) Messen Sie die Höhe von der Spitze der Pyramide bis zur Mitte der Basis; C) A mit B multiplizieren; D) dividiere durch 3.
Insgesamt gewöhnliche Pyramiden sind die aufrechten Rippen, die Linie, die die dreieckige Seite in zwei gleiche Dreiecke teilt und die Breite der Basis, die durch den Satz des Pythagoras verbunden ist: (Länge der Seite ÷ 2) + (Länge der Rippe) = (Höhe)

Warnungen

Pyramiden haben drei Arten von Höhen: die Linie, die die dreieckige Fläche in zwei gleiche Dreiecke teilt, die Länge der Rippe (entlang der Seite einer dreieckigen Fläche) und die tatsächliche Höhe (von der Spitze der Pyramide senkrecht zur Basis). .).