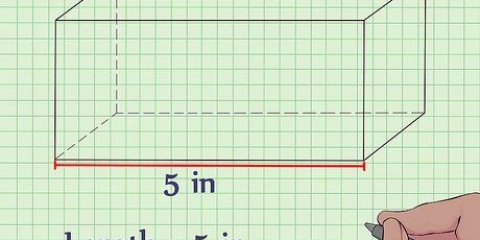
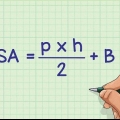Im Beispiel betragen die Seiten der Basis der Pyramide alle 5 cm, und Sie berechnen die Fläche der Basis wie folgt: 
Denken Sie daran, dass zweidimensionale Flächen in Quadraten ausgedrückt werden – Quadratzentimeter, Meter, Kilometer usw. 
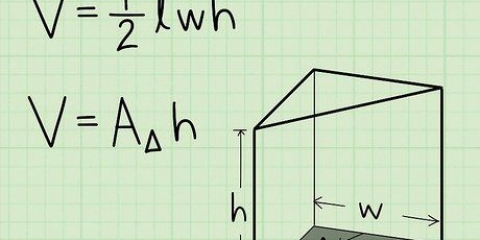
Im Beispiel nehmen wir an, dass die Pyramide eine Höhe von 9 cm . hat. Multiplizieren Sie in diesem Fall die Fläche der Basis wie folgt mit diesem Wert: 
Denken Sie daran, dass Volumen in Kubikeinheiten ausgedrückt werden. Da in diesem Fall alle Längenmaße Zentimeter sind, wird das Volumen in Kubikzentimetern angegeben. 
Teilen Sie im Beispiel 225 cm durch 3 und das Ergebnis ist 75 cm für das Volumen. 


Diese Ersetzung sieht so aus: 


 .....(Originalgleichung)
.....(Originalgleichung) .....(beide Seiten rechtwinklig)
.....(beide Seiten rechtwinklig) .....(Werte eingeben)
.....(Werte eingeben) .....(vereinfachen Bruch)
.....(vereinfachen Bruch) .....(Viereck vereinfachen)
.....(Viereck vereinfachen) .....(subtrahieren)
.....(subtrahieren) .....(vereinfachen Wurzel)
.....(vereinfachen Wurzel)
Aus den Berechnungen leiten wir ab, dass die Höhe der Pyramide 12 cm beträgt. Verwenden Sie dies zusammen mit der 10 cm langen Seite der Basis, um das Volumen der Pyramide zu berechnen: 









 ..........(angepasste Gleichung)
..........(angepasste Gleichung) ..........(Ersetzen Sie h auf beiden Seiten)
..........(Ersetzen Sie h auf beiden Seiten) ..........(Subtrahieren Sie die Quadratwurzel von beiden Seiten)
..........(Subtrahieren Sie die Quadratwurzel von beiden Seiten) ..........(tragen Sie die Zahlen ein)
..........(tragen Sie die Zahlen ein) ..........(vereinfache die Quadrate)
..........(vereinfache die Quadrate) ..........(Werte abziehen)
..........(Werte abziehen) ..........(vereinfache die Quadratwurzel)
..........(vereinfache die Quadratwurzel)Verdoppeln Sie diesen Wert, um die Diagonale der quadratischen Grundfläche der Pyramide zu ermitteln. Somit beträgt die Diagonale der Pyramidenbasis 9,8 * 2 = 19,6 cm. 
In diesem Pyramidenbeispiel beträgt die Diagonale der Basis 19,6 cm. Daher ist die Seite gleich: 





Berechnung des volumens einer quadratischen pyramide
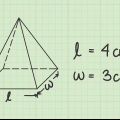
Eine quadratische Pyramide ist eine dreidimensionale Figur mit einer quadratischen Grundfläche und dreieckigen Schrägen, die sich an einem Punkt über der Grundfläche treffen. Für den Fall, dass 


Schritte
Methode 1 von 3: Bestimmen Sie das Volumen mit der Grundfläche und der Höhe

1. Messen Sie die Länge der Seite der Basis. Da quadratische Pyramiden per Definition eine quadratische Grundfläche haben, sollten alle Seiten der Grundfläche gleich lang sein. Bei einer quadratischen Pyramide müssen Sie also nur die Länge einer der Seiten kennen.
- Angenommen, Sie haben eine Pyramide mit quadratischer Grundfläche, deren Seiten eine Länge von . haben
. Sie verwenden diesen Wert, um die Fläche der Basis zu berechnen.
- Wenn die Seiten der Basis nicht gleich lang sind, haben Sie a rechteckige Pyramide statt einer quadratischen Pyramide. Die Formel für das Volumen einer rechteckigen Pyramide ist der Formel für quadratische Pyramiden sehr ähnlich. Für den Fall, dass
ist die Länge der Basis der rechteckigen Pyramide und
die Breite, dann das Volumen der Pyramide
.

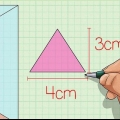
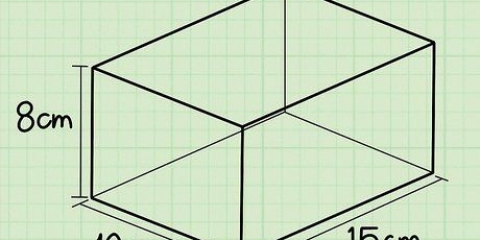
2. Berechnen Sie die Fläche der Basis. Um das Volumen zu bestimmen, benötigt man zunächst die Fläche des Sockels. Sie tun dies, indem Sie die Länge und Breite der Basis multiplizieren. Da die Basis einer quadratischen Pyramide ein Quadrat ist, haben alle Seiten die gleiche Länge und die Fläche der Basis ist gleich dem Quadrat der Länge einer ihrer Seiten (also mit sich selbst multipliziert).


3. Multiplizieren Sie die Fläche der Basis mit der Höhe der Pyramide. Dann multipliziert man die Grundfläche mit der Höhe der Pyramide. Zur Erinnerung, die Höhe ist der Abstand ist die Länge des Liniensegments von der Spitze der Pyramide bis zur Basis, im rechten Winkel.


4. Teile diese Antwort durch 3. Schließlich bestimmen Sie das Volumen der Pyramide, indem Sie den gerade gefundenen Wert (indem Sie die Fläche der Basis mit der Höhe multiplizieren) durch 3 . teilen. Dies berechnet das Volumen der quadratischen Pyramide.
Methode 2 von 3: Bestimmen Sie das Volumen mit dem Apothem

1. Messen Sie das Apothem der Pyramide. Manchmal ist die senkrechte Höhe der Pyramide nicht angegeben (oder Sie müssen sie messen), sondern das Apothem. Mit dem Apothem kannst du die Satz des Pythagoras verwenden, um die senkrechte Höhe zu berechnen.
- Das Apothem einer Pyramide ist der Abstand von der Spitze zur Mitte einer der Seiten ihrer Basis. Messen Sie bis zur Mitte einer der Seiten und nicht bis zu einer der Ecken der Basis. Für dieses Beispiel nehmen wir an, dass ein Apothem 13 cm beträgt und die Länge einer Seite der Basis 10 cm beträgt.
- Denken Sie daran, dass der Satz des Pythagoras ausgedrückt werden kann als die Gleichung
, wodurch
und
die senkrechten Schenkel sind vom rechtwinkligen Dreieck und
die Hypotenuse.

2. Stellen Sie sich ein rechtwinkliges Dreieck vor. Um den Satz des Pythagoras zu verwenden, benötigen Sie ein rechtwinkliges Dreieck. Stellen Sie sich ein Dreieck vor, das die Pyramide in zwei Hälften teilt und senkrecht zur Basis der Pyramide steht. Das Apothem der Pyramide, genannt  , ist die Hypotenuse dieses rechtwinkligen Dreiecks. Die Basis dieses rechtwinkligen Dreiecks ist halb so lang wie
, ist die Hypotenuse dieses rechtwinkligen Dreiecks. Die Basis dieses rechtwinkligen Dreiecks ist halb so lang wie  , die Seite der quadratischen Grundfläche der Pyramide.
, die Seite der quadratischen Grundfläche der Pyramide.
 , ist die Hypotenuse dieses rechtwinkligen Dreiecks. Die Basis dieses rechtwinkligen Dreiecks ist halb so lang wie
, ist die Hypotenuse dieses rechtwinkligen Dreiecks. Die Basis dieses rechtwinkligen Dreiecks ist halb so lang wie  , die Seite der quadratischen Grundfläche der Pyramide.
, die Seite der quadratischen Grundfläche der Pyramide.
3. Weisen Sie den Werten Variablen zu. Der Satz des Pythagoras verwendet die Variablen a, b und c, aber es ist hilfreich, sie durch Variablen zu ersetzen, die für Ihr Problem von Bedeutung sind. das apotheme  tritt an die Stelle von
tritt an die Stelle von  im Satz des Pythagoras. Der Schenkel des rechtwinkligen Dreiecks (
im Satz des Pythagoras. Der Schenkel des rechtwinkligen Dreiecks ( ), tritt an die Stelle von
), tritt an die Stelle von  Du gehst die Höhe
Du gehst die Höhe  bestimme die Pyramide, die den Platz von einnimmt
bestimme die Pyramide, die den Platz von einnimmt  im Satz des Pythagoras.
im Satz des Pythagoras.
 tritt an die Stelle von
tritt an die Stelle von  im Satz des Pythagoras. Der Schenkel des rechtwinkligen Dreiecks (
im Satz des Pythagoras. Der Schenkel des rechtwinkligen Dreiecks ( ), tritt an die Stelle von
), tritt an die Stelle von  Du gehst die Höhe
Du gehst die Höhe  bestimme die Pyramide, die den Platz von einnimmt
bestimme die Pyramide, die den Platz von einnimmt  im Satz des Pythagoras.
im Satz des Pythagoras.


4. Verwenden Sie den Satz des Pythagoras, um die senkrechte Höhe zu berechnen. Verwenden Sie die gemessenen Werte  und
und  . Dann löse die Gleichung:
. Dann löse die Gleichung:
 und
und  . Dann löse die Gleichung:
. Dann löse die Gleichung: .....(Originalgleichung)
.....(Originalgleichung) .....(beide Seiten rechtwinklig)
.....(beide Seiten rechtwinklig) .....(Werte eingeben)
.....(Werte eingeben) .....(vereinfachen Bruch)
.....(vereinfachen Bruch) .....(Viereck vereinfachen)
.....(Viereck vereinfachen) .....(subtrahieren)
.....(subtrahieren) .....(vereinfachen Wurzel)
.....(vereinfachen Wurzel)
5. Verwenden Sie Höhe und Basis, um das Volumen zu berechnen. Nachdem Sie diese Berechnungen auf den Satz des Pythagoras angewendet haben, haben Sie nun die Informationen, die Sie benötigen, um das Volumen der Pyramide zu berechnen. Verwenden Sie die Formel  und lösen Sie diese, achten Sie darauf, dass Sie die Antwort in Quadrateinheiten angeben.
und lösen Sie diese, achten Sie darauf, dass Sie die Antwort in Quadrateinheiten angeben.
 und lösen Sie diese, achten Sie darauf, dass Sie die Antwort in Quadrateinheiten angeben.
und lösen Sie diese, achten Sie darauf, dass Sie die Antwort in Quadrateinheiten angeben.



Methode 3 von 3: Bestimmen des Volumens mit der Höhe der Beine

1. Messen Sie die Höhe der Beine der Pyramide. Die Höhe der Beine ist die Länge der Kanten der Pyramide, gemessen von der Spitze bis zu einer der Ecken der Basis. Verwenden Sie wie oben den Satz des Pythagoras, um die senkrechte Höhe der Pyramide zu berechnen.
- In diesem Beispiel nehmen wir an, dass die Höhe der Beine 11 cm beträgt und die senkrechte Höhe 5 cm beträgt.

2. Stellen Sie sich ein rechtwinkliges Dreieck vor. Auch hier benötigen Sie ein rechtwinkliges Dreieck, um den Satz des Pythagoras anwenden zu können. In diesem Fall ist der unbekannte Wert jedoch die Basis der Pyramide. Bekannt ist die vertikale Höhe und die Höhe der Beine. Stellen Sie sich nun vor, die Pyramide diagonal von einer Ecke zur anderen zu schneiden und dann die Figur zu öffnen, die resultierende Ebene würde wie ein Dreieck aussehen. Die Höhe dieses Dreiecks ist die senkrechte Höhe der Pyramide. Dies teilt das exponierte Dreieck in zwei symmetrische rechtwinklige Dreiecke. Die Hypotenuse jedes der rechtwinkligen Dreiecke ist die Höhe der Beine der Pyramide. Die Basis jedes der rechtwinkligen Dreiecke ist die halbe Diagonale der Basis der Pyramide.

3. Variablen zuweisen. Verwenden Sie das imaginäre rechtwinklige Dreieck und weisen Sie dem Satz des Pythagoras Werte zu. Du kennst die vertikale Höhe,  das ist eine Seite des Satzes des Pythagoras,
das ist eine Seite des Satzes des Pythagoras,  . Die Höhe der Beine der Pyramide,
. Die Höhe der Beine der Pyramide,  bildet die Hypotenuse dieses imaginären rechtwinkligen Dreiecks und tritt damit an die Stelle von
bildet die Hypotenuse dieses imaginären rechtwinkligen Dreiecks und tritt damit an die Stelle von  . Die unbekannte Diagonale der Pyramidenbasis ist die verbleibende Seite des rechtwinkligen Dreiecks,
. Die unbekannte Diagonale der Pyramidenbasis ist die verbleibende Seite des rechtwinkligen Dreiecks,  Nach diesen Ersetzungen sieht die Gleichung wie folgt aus:
Nach diesen Ersetzungen sieht die Gleichung wie folgt aus:
 das ist eine Seite des Satzes des Pythagoras,
das ist eine Seite des Satzes des Pythagoras,  . Die Höhe der Beine der Pyramide,
. Die Höhe der Beine der Pyramide,  bildet die Hypotenuse dieses imaginären rechtwinkligen Dreiecks und tritt damit an die Stelle von
bildet die Hypotenuse dieses imaginären rechtwinkligen Dreiecks und tritt damit an die Stelle von  . Die unbekannte Diagonale der Pyramidenbasis ist die verbleibende Seite des rechtwinkligen Dreiecks,
. Die unbekannte Diagonale der Pyramidenbasis ist die verbleibende Seite des rechtwinkligen Dreiecks,  Nach diesen Ersetzungen sieht die Gleichung wie folgt aus:
Nach diesen Ersetzungen sieht die Gleichung wie folgt aus:


4. Berechnen Sie die Diagonale der quadratischen Grundfläche. Sie müssen die Gleichung neu anordnen, um die Variable zu erhalten  isolieren und dann seinen Wert berechnen.
isolieren und dann seinen Wert berechnen.
 isolieren und dann seinen Wert berechnen.
isolieren und dann seinen Wert berechnen. ..........(angepasste Gleichung)
..........(angepasste Gleichung) ..........(Ersetzen Sie h auf beiden Seiten)
..........(Ersetzen Sie h auf beiden Seiten) ..........(Subtrahieren Sie die Quadratwurzel von beiden Seiten)
..........(Subtrahieren Sie die Quadratwurzel von beiden Seiten) ..........(tragen Sie die Zahlen ein)
..........(tragen Sie die Zahlen ein) ..........(vereinfache die Quadrate)
..........(vereinfache die Quadrate) ..........(Werte abziehen)
..........(Werte abziehen) ..........(vereinfache die Quadratwurzel)
..........(vereinfache die Quadratwurzel)
5. Finden Sie die Seite der Basis der Diagonalen. Die Basis der Pyramide ist ein Quadrat. Die Diagonale jedes Quadrats ist gleich der Länge einer seiner Seiten mal Quadratwurzel 2. Und so können Sie die Seite eines Quadrats finden, indem Sie die Diagonale durch die Quadratwurzel 2 . dividieren.


6. Berechnen Sie das Volumen anhand der Seite und Höhe. Kehren Sie zur ursprünglichen Formel zurück, um das Volumen anhand der seitlichen und senkrechten Höhe zu berechnen.




Tipps
- In einer quadratischen Pyramide können die senkrechte Höhe, das Apothem und die Länge der Kante der Basis alle mit dem Satz des Pythagoras berechnet werden.
"Berechnung des volumens einer quadratischen pyramide"
Оцените, пожалуйста статью