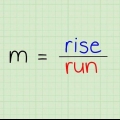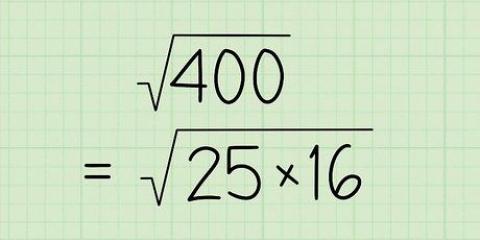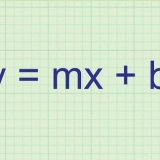Die x-Achse ist die horizontale Achse; die y-Achse ist die vertikale Achse. Die Koordinaten eines Punktes werden geschrieben als  .
. Ein Liniensegment kann beispielsweise einen Endpunkt bei haben  und noch einer auf
und noch einer auf  .
. 
Zum Beispiel mit den Punkten  und
und  , deine formel sieht dann so aus:
, deine formel sieht dann so aus: 


Zum Beispiel:



Zum Beispiel:



Da Sie die Quadratwurzel bestimmen, müssen Sie Ihre Antwort möglicherweise runden. Da Sie von einem Koordinatensystem aus arbeiten, lautet Ihre Antwort im Allgemeinen "Einheiten" und nicht in Zentimetern, Metern oder anderen Einheiten. Zum Beispiel:

 Einheiten.
Einheiten.
Berechnung der länge einer linie mit der distanzformel
Sie können die Länge einer vertikalen oder horizontalen Linie in einem Koordinatensystem messen, indem Sie einfach die Koordinaten addieren; Die Länge einer diagonalen Linie zu messen ist jedoch etwas schwieriger. Mit der Abstandsformel können Sie die Länge einer solchen Linie ermitteln. Diese Formel ist eigentlich der Satz des Pythagoras, der deutlich wird, wenn man sich den Geradenabschnitt als Hypotenuse eines rechtwinkligen Dreiecks vorstellt. Durch die Verwendung einer einfachen geometrischen Formel wird das Messen von Linien entlang einer Reihe von Koordinaten zu einer relativ einfachen Aufgabe.
Schritte
Teil 1 von 2: Formel schreiben

1. Schreibe die Distanzformel auf. Die Formel besagt, dass  , wodurch
, wodurch  ist gleich dem Abstand der Linie,
ist gleich dem Abstand der Linie,  gleich den Koordinaten des ersten Endpunkts des Liniensegments ist und
gleich den Koordinaten des ersten Endpunkts des Liniensegments ist und  gleich den Koordinaten des zweiten Endpunktes des Liniensegments.
gleich den Koordinaten des zweiten Endpunktes des Liniensegments.
 , wodurch
, wodurch  ist gleich dem Abstand der Linie,
ist gleich dem Abstand der Linie,  gleich den Koordinaten des ersten Endpunkts des Liniensegments ist und
gleich den Koordinaten des ersten Endpunkts des Liniensegments ist und  gleich den Koordinaten des zweiten Endpunktes des Liniensegments.
gleich den Koordinaten des zweiten Endpunktes des Liniensegments.
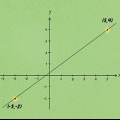
2. Bestimmen Sie die Koordinaten der Endpunkte des Liniensegments. Diese wurden möglicherweise schon vergeben. Wenn nicht, zählen Sie entlang der x- und y-Achse, um die Koordinaten zu finden.
 .
. und noch einer auf
und noch einer auf  .
.
3. Wenden Sie die Koordinaten auf die Entfernungsformel an. Stellen Sie sicher, dass Sie die Werte für die richtigen Variablen eingeben. Die Zwei  -Koordinaten stehen in den ersten Klammern und die beiden
-Koordinaten stehen in den ersten Klammern und die beiden  -Koordinaten sind innerhalb der nächsten zwei Klammern.
-Koordinaten sind innerhalb der nächsten zwei Klammern.
 -Koordinaten stehen in den ersten Klammern und die beiden
-Koordinaten stehen in den ersten Klammern und die beiden  -Koordinaten sind innerhalb der nächsten zwei Klammern.
-Koordinaten sind innerhalb der nächsten zwei Klammern. und
und  , deine formel sieht dann so aus:
, deine formel sieht dann so aus: 
Teil 2 von 2: Berechnung der Entfernung

1. Berechne die Minussumme in Klammern. Gemäß der Reihenfolge der Operationen muss jede Berechnung in Klammern zuerst berechnet werden.
- Zum Beispiel:

2. Den Wert in Klammern quadrieren. Die Operationsreihenfolge besagt, dass man dann die Potenzen berechnen muss.



3. Füge die Zahlen unter dem Radikalzeichen hinzu. Sie können diese Berechnung durchführen, als ob Sie mit ganzen Zahlen arbeiten würden.



4. Lösen für D  . Um die endgültige Antwort anzunähern, finden Sie die Quadratwurzel der Summe unter dem Radikal.
. Um die endgültige Antwort anzunähern, finden Sie die Quadratwurzel der Summe unter dem Radikal.
 . Um die endgültige Antwort anzunähern, finden Sie die Quadratwurzel der Summe unter dem Radikal.
. Um die endgültige Antwort anzunähern, finden Sie die Quadratwurzel der Summe unter dem Radikal.
 Einheiten.
Einheiten.Tipps
- Verwechseln Sie diese Formel nicht mit anderen, wie der Mittelpunktsformel, der Steigungsformel oder der Geradengleichung.
- Beachten Sie die Reihenfolge der Operationen, wenn Sie die Antwort berechnen. Erst subtrahieren, dann die Differenz quadrieren, dann addieren und dann die Quadratwurzel berechnen.
"Berechnung der länge einer linie mit der distanzformel"
Оцените, пожалуйста статью