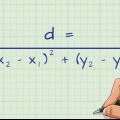Kostenlose Schritt für Schritt Anweisungen 
Z.B.: 10 - 9 = 1 
Z.B.: -1/10 = -0.1 
Z.B.: |-0.1| = 0.1 
Z.B.: 0.1 x 100 = 10 %
Berechnung einer fehlerrate
Die Berechnung eines Fehlerprozentsatzes kann mit der Schätzung eines genauen Wertes verglichen werden. Die Fehlerquote ist die Differenz zwischen den geschätzten Werten und genauen Werten als Prozentsatz des genauen Wertes, und Sie können damit sehen, wie nahe Ihre Schätzung am tatsächlichen Wert liegt. Wenn Sie die Fehlerquote einer Schätzung berechnen möchten, brauchen Sie nur den geschätzten Wert und den genauen Wert, und schon kann es losgehen.
Schritte
1. Lernen Sie die Formel zur Berechnung der Fehlerquote. Die Formel zur Berechnung der Fehlerquote lautet wie folgt:“[(|Genauer Wert-Schätzwert|)/Genauer Wert] x 100
- Der geschätzte Wert ist ein Näherungswert und der genaue Wert ist der tatsächliche Wert. Sobald Sie den absoluten Wert der Differenz zwischen dem geschätzten Wert und dem genauen Wert gefunden haben, müssen Sie ihn nur noch durch den genauen Wert dividieren und das Ergebnis mit 100 . multiplizieren.
2. Ziehen Sie den tatsächlichen Wert von Ihrem eigenen Wert ab. Das bedeutet, dass Sie den tatsächlichen Wert vom geschätzten Wert abziehen müssen. In diesem Fall beträgt der tatsächliche Wert 10 und der geschätzte Wert 9.
3. Teilen Sie das Ergebnis durch die tatsächliche Zahl. Dividiere -1 (das Ergebnis von 9 – 10) durch 10 (den tatsächlichen Wert). Gib den Bruch in Dezimalform ein.
4. Bestimmt den Absolutwert des Ergebnisses. Der Absolutwert einer Zahl ist der positive Wert der Zahl, sei er positiv oder negativ. Der Absolutwert einer positiven Zahl ist die Zahl selbst, und der Absolutwert einer negativen Zahl ist einfach der Wert dieser Zahl ohne Minuszeichen (damit die negative Zahl positiv wird).
5. Multiplizieren das Ergebnis mit 100. Also nur 0,1 (das Ergebnis) x 100. Zeigt die Antwort als Prozentsatz an. Setzen Sie ein Prozentzeichen hinter die Antwort und fertig.
Tipps
- Einige Lehrer möchten, dass Sie die Fehlerquote auf einen bestimmten Punkt aufrunden; die meisten werden mit einer auf drei signifikante Stellen gerundeten Fehlerrate zufrieden sein.
Оцените, пожалуйста статью
