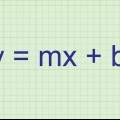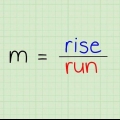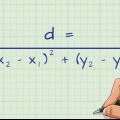Neigung und Schnittpunkte einer Linie berechnen

Schritte

Die Steigung einer Linie misst, wie steil die Linie ist.Man könnte auch sagen, dass es der Abstand auf der y-Achse im Vergleich zum Abstand auf der x-Achse ist – d. h. wie stark die Linie vertikal im Verhältnis zu ihrer horizontalen Zunahme ansteigt. In der Lage zu sein, die Steigung einer Linie zu finden oder die Steigung zu verwenden, um Punkte auf der Linie zu finden, ist eine wichtige Fähigkeit, die in Mathematik, Wirtschaft, Naturwissenschaften, Rechnungswesen/Finanzen und anderen Bereichen verwendet wird.

Schritte

Methode 1 von 4: Verwenden eines Diagramms zum Ermitteln der Steigung

Bildtitel Calculate Slope and Intercepts of a Line Step 1

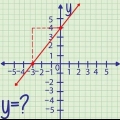
1. Wähle zwei Punkte auf der Linie. Zeichnen Sie Punkte in die Grafik, um diese Punkte darzustellen, und notieren Sie ihre Koordinaten.

Vergessen Sie beim Zeichnen von Punkten nicht, zuerst die x-Koordinate und dann die y-Koordinate anzugeben.
Zum Beispiel: Sie könnten die Punkte (-3, -2) und (5, 4) wählen.

Bildtitel Calculate Slope and Intercepts of a Line Step 2

2. Finden Sie den Anstieg zwischen den beiden Punkten. Dazu müssen Sie die Differenz in y der beiden Punkte vergleichen. Beginnen Sie mit dem ersten Punkt, dem Punkt ganz links im Diagramm, und zählen Sie, bis Sie die y-Koordinate des zweiten Punktes erreichen.

Der Anstieg kann positiv oder negativ sein; das heißt, Sie müssen auf- oder abzählen, um es zu finden. Wenn sich die Linie nach oben und rechts bewegt, ist der Anstieg positiv. Wenn sich die Linie nach unten und rechts bewegt, ist der Anstieg negativ.

Wenn beispielsweise die y-Koordinate des ersten Punkts (-2) und die y-Koordinate des zweiten Punkts (4) ist, dann addieren Sie sechs Punkte und der Anstieg beträgt 6.

Bildtitel Calculate Slope and Intercepts of a Line Step 3

3. Bestimmen Sie den horizontalen Abstand zwischen den beiden Punkten. Dazu müssen Sie die Differenz der x-Werte der beiden Punkte vergleichen. Beginnen Sie mit dem ersten Punkt, dem Punkt, der am weitesten links vom Graphen liegt, und zählen Sie, bis Sie die x-Koordinate des zweiten Punktes erreichen.

Der horizontale Abstand ist immer positiv; das heißt, man kann nur von links nach rechts zählen, niemals von rechts nach links.

Wenn beispielsweise die x-Koordinate des ersten Punkts (-3) ist und die x-Koordinate des zweiten Punkts (5) ist, dann würden Sie eine Entfernung von 8 . zählen.

Bildtitel Calculate Slope and Intercepts of a Line Step 4

4. Bilden Sie ein Verhältnis y/x, um die Steigung zu finden. Die Steigung ist normalerweise ein Bruch, kann aber auch eine ganze Zahl sein.

Wenn beispielsweise der Anstieg 6 und der Abfall 8 beträgt, ist Ihre Steigung

\frac{6}{8}

${displaystyle {frac {6}{8}}}$ , was vereinfacht werden kann zu

\frac{3}{4}

${frac{3}{4}}$ .

Methode 2 von 4: Verwenden von zwei gegebenen Punkten, um die Steigung zu finden

Bildtitel Calculate Slope and Intercepts of a Line Step 5

1. Schreiben Sie die folgende Formel:

m = ja 2 - {ja}_{1} x 2 - x_{1}

${displaystyle m={frac {y_{2}-y_{1}}{x_{2}-x_{1}}}}$ . In dieser Formel ist `m` die Steigung,

(x 1, {ja}_{1})

$(x_{{1}},y_{{1}})$ sind die Koordinaten des ersten Punktes,

(x 2, {ja}_{2})

$(x_{{2}},y_{{2}})$ sind die Koordinaten des zweiten Punktes.

Denken Sie daran, dass die Steigung gleich ist $\frac{ja}{x}$ ${frac{y}{x}}$ . Sie verwenden diese Formel, um die Änderung von y (Anstieg) über die Änderung von x (Entfernung) zu ermitteln.

Bildtitel Calculate Slope and Intercepts of a Line Step 6

2. Setze die x- und y-Koordinaten in die Formel ein. Stellen Sie sicher, dass Sie die Koordinaten des ersten Punktes (

(x 1, {ja}_{1})

$(x_{{1}},y_{{1}})$ ) und der zweite Punkt (

(x 2, {ja}_{2})

$(x_{{2}},y_{{2}})$ ) an den richtigen Stellen in der Formel, sonst berechnen Sie nicht die richtige Steigung.

Mit den Punkten (-3, -2) und (5, 4) sieht Ihre Formel beispielsweise so aus:

m = 4 - (- 2) 5 - (- 3)

${displaystyle m={frac {4-(-2)}{5-(-3)}}}$ .

Bildtitel Calculate Slope and Intercepts of a Line Step 7

3. Vervollständigen Sie die Berechnung und vereinfachen Sie wenn möglich. Dadurch erhalten Sie die Steigung als Bruch oder ganze Zahl.

Zum Beispiel: mit einer Steigung

m = 4 - (- 2) 5 - (- 3)

${displaystyle m={frac {4-(-2)}{5-(-3)}}}$ berechnest du?

4 - (- 2) = 6

${displaystyle 4-(-2)=6}$ im Zähler ((denken Sie daran, beim Subtrahieren einer negativen Zahl zu addieren) und

5 - (- 3) = 8

${displaystyle 5-(-3)=8}$ im Nenner. Du hast vereinfacht

\frac{6}{8}

${displaystyle {frac {6}{8}}}$ dann zu

\frac{3}{4}

${frac{3}{4}}$ , und somit

m = \frac{3}{4}

${displaystyle m={frac {3}{4}}}$ .

Methode 3 von 4: Bestimmen des Schnittpunkts mit der y-Achse bei gegebener Steigung und einem Punkt

Bildtitel Calculate Slope and Intercepts of a Line Step 8

1. Setze die Formel ja=mx+B{displaystyle y=mx+b} ${displaystyle y=mx+b}$ an. In der Formel ist y die y-Koordinate eines beliebigen Punktes auf der Geraden, m ist die Steigung, x ist die x-Koordinate eines beliebigen Punktes auf der Geraden und b ist der Schnittpunkt mit der y-Achse.

$ja = m x + B$ $y=mx+b$ ist die Geradengleichung.
Der Schnittpunkt mit der y-Achse ist der Punkt, an dem die Linie die y-Achse schneidet.

EXPERTENTIPP

Grace Imson, MA

Mathematiklehrerin am City College of San FranciscoGrace Imson ist Mathematiklehrerin mit über 40 Jahren Erfahrung. Derzeit unterrichtet sie Mathematik am City College of San Francisco und war zuvor an der Fakultät für Mathematik der Saint Louis University tätig. Grace hat Mathematik in der Grundschule, in der High School und am College unterrichtet. Sie hat einen Master-Abschluss in Erziehungswissenschaften mit Spezialisierung auf Schulmanagement und Supervision von der Saint Louis University.

Grace Imson, MA
Mathematiklehrer am City College of San Francisco

Unser Experte erklärt:` Wenn Sie die Steigung und einen Punkt haben, berücksichtigen Sie dies in der Geradengleichung. In y = mx + b ist m die Steigung und die Koordinaten des Punktes enthalten sowohl x als auch y. Dann nach b auflösen, um den Schnittpunkt mit der y-Achse zu finden.

Bildtitel Calculate Slope and Intercepts of a Line Step 9

2. Verarbeiten Sie die Steigung und die Koordinaten eines Punktes in der Linie. Denken Sie daran, dass die Steigung gleich der Steigung über die horizontale Distanz ist. Wenn Sie Hilfe bei der Suche nach der Piste benötigen, lesen Sie die Anweisungen oben.

Zum Beispiel: wenn die Steigung gleich ist

\frac{3}{4}

${frac{3}{4}}$ , und ein Punkt auf der Geraden ist (5.4), dann sieht die Formel so aus:

4 = \frac{3}{4} (5) + B

${displaystyle 4={frac {3}{4}}(5)+b}$ .

Bildtitel Calculate Slope and Intercepts of a Line Step 10

3. Löse die Gleichung nach b. Multiplizieren Sie zuerst die Steigung und die x-Koordinate. Subtrahiere diese Zahl von beiden Seiten, um nach b . aufzulösen.

Im Beispielproblem wird die Gleichung

4 = 3 \frac{3}{4} + B

${displaystyle 4=3{frac {3}{4}}+b}$ . wenn du

3 \frac{3}{4}

${displaystyle 3{frac {3}{4}}}$ subtrahiert von beiden Seiten, am Ende hast du

\frac{1}{4} = B

${displaystyle {frac {1}{4}}=b}$ . Der Schnittpunkt mit der y-Achse ist also gleich

\frac{1}{4}

${frac{1}{4}}$ .

Bildtitel Calculate Slope and Intercepts of a Line Step 11

4. Überprüfe deine Arbeit. Zeichnen Sie den bekannten Punkt in einem Diagramm und zeichnen Sie dann eine Linie mit der Steigung (der Steigung). Um den Schnittpunkt mit der y-Achse zu finden, suchen Sie den Punkt, an dem die Linie die y-Achse schneidet.

Zum Beispiel: wenn die Steigung

\frac{3}{4}

${frac{3}{4}}$ ist, und ein Punkt ist (5.4), dann zeichne einen Punkt nach oben (5.4), dann zeichne andere Punkte entlang der Linie, indem du vier nach links und drei nach unten gehst. Wenn Sie eine Linie durch die Punkte ziehen, sollte die Linie die y-Achse knapp über der (0,0)-Koordinate schneiden.

Methode 4 von 4: Bestimmen des Schnittpunkts mit der x-Achse, gegeben der Steigung und dem Schnittpunkt mit der y-Achse

Bildtitel Calculate Slope and Intercepts of a Line Step 12

$ja = m x + B$ $y=mx+b$ ist die Geradengleichung.
Der Schnittpunkt mit der x-Achse ist der Punkt, an dem die Linie die x-Achse schneidet.

Bildtitel Calculate Slope and Intercepts of a Line Step 13

2. Wenden Sie die Steigung und den Schnittpunkt mit der y-Achse auf die Formel an. Denken Sie daran, dass die Steigung gleich der Steigung über die horizontale Distanz ist. Wenn Sie Hilfe bei der Suche nach der Piste benötigen, lesen Sie die Anweisungen oben.

Zum Beispiel: die Steigung ist

\frac{3}{4}

${frac{3}{4}}$ , und der Schnittpunkt mit der y-Achse ist

\frac{1}{4}

${frac{1}{4}}$ , also sieht die formel so aus:

ja = \frac{3}{4} x + \frac{1}{4}

${displaystyle y={frac {3}{4}}x+{frac {1}{4}}}$ .

Bildtitel Calculate Slope and Intercepts of a Line Step 14

3. y auf 0 setzen.Sie suchen den Schnittpunkt mit der x-Achse, den Punkt, an dem die Linie die x-Achse schneidet. An diesem Punkt ist die y-Koordinate null. Wenn wir also y auf 0 setzen und nach der entsprechenden x-Koordinate auflösen, finden wir den Punkt (x, 0), der der Schnittpunkt mit der x-Achse ist.

Im Beispielproblem wird die Gleichung

0 = \frac{3}{4} x + \frac{1}{4}

${displaystyle 0={frac {3}{4}}x+{frac {1}{4}}}$ .

Bildtitel Calculate Slope and Intercepts of a Line Step 15

4. Vervollständigen Sie die Gleichung, indem Sie nach x . auflösen. Subtrahiere zuerst den Schnittpunkt mit der y-Achse von beiden Seiten. Dann beide Seiten durch die Neigung teilen.

Im Beispielproblem wird die Gleichung

- 1 4 = \frac{3}{4} x

${displaystyle {frac {-1}{4}}={frac {3}{4}}x}$ . Teilen Sie beide Seiten

\frac{3}{4}

${frac{3}{4}}$ , und du bekommst

- 4 12 = x

${displaystyle {frac {-4}{12}}=x}$ . Dies ist vereinfacht zu

- 1 3 = x

${displaystyle {frac {-1}{3}}=x}$ . Der Schnittpunkt mit der x-Achse ist also

(- 1 3, 0)

${displaystyle ({frac {-1}{3}},0)}$ . Daher

- 1 3

${displaystyle {frac {-1}{3}}}$ .

Bildtitel Calculate Slope and Intercepts of a Line Step 16

5. Überprüfe deine Arbeit. Zeichne den Schnittpunkt mit der y-Achse und zeichne dann eine Linie mit der Steigung. Um den Schnittpunkt mit der x-Achse zu finden, suchen Sie den Punkt, an dem die Linie die x-Achse schneidet.

Zum Beispiel: wenn die Steigung

\frac{3}{4}

${frac{3}{4}}$ ist , und der Schnittpunkt mit der y-Achse

(0, \frac{1}{4})

${displaystyle (0,{frac {1}{4}})}$ , dann zeichne den Punkt

(0, \frac{1}{4})

${displaystyle (0,{frac {1}{4}})}$ , und zeichnen Sie dann weitere Punkte entlang der Linie, indem Sie 4 nach links und 3 nach unten und 3 nach rechts und 4 nach oben zählen. Wenn Sie eine Linie durch die Punkte ziehen, sehen Sie, dass die Linie die x-Achse direkt links von der (0,0)-Koordinate schneidet.